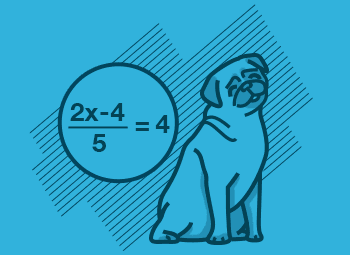What is calculus?

Calculus math is the branch of mathematics involved with studying the rate of change, motion, and limits. As a joint discovery in Mathematics, Sir Isaac Newton and Gottfried Newbitz are credited as the Fathers of calculus for their early work in developing the fundamental concepts, theories and calculus rules we study today. Recent findings in the past decade however, suggest that this honour must now be split 4-fold to include Madhava and Nilakantha on the throne. Sir Isaac Newton was responsible for establishing the relationship between the two key topics in calculus: Differentials and Integrals. Gottfried Newbitz work was more focused on the rate of change in graphs alongside developing the mathematical notation for calculus that we use today. Research has now confirmed that Madhava and Nilakantha were responsible for discovering infinite series in calculus, two centuries before Sir Isaac Newton and Gottfried Newbitz were born.

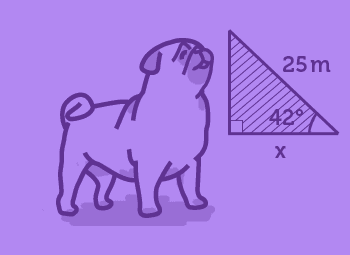
If you're just getting started with basic calculus or intro to calculus, differential calculus is the first order of business. Here you will learn how to calculate the slope of curves (e.g. parabolas), learn to use and apply the different derivative rules, and identify rates of change in velocity and acceleration.

In Calculus 1, Business Calculus, or any of your AP Calculus classes, you will also take a closer look at the concepts of limits and infinity. On the surface, these concepts appear to be at odds with one another. In the world of calculus however, this is far from true. Finding the limits of any graph requires you to look at what is happening at the microscopic level, dissecting the graph into infinitely small pieces and examining what happens as points on a graph get infinitesimally close together. These foundational notions links differentials and integrals together.

Integral Calculus falls into the realm of advanced calculus. Topics covered here you'll likely see in AP Calculus AB, but more so in AP Calculus BC and Calculus 2. Integral calculus is where you learn new methods of calculating area, volume and arc lengths of objects, learn integration techniques, and apply calculus to sequences and series. Science, Technology, Math, and Engineering (STEM) majors may be required to study differential equations, a higher level of specialized topics related to differential calculus. Here you will examine first and second order differential equations alongside Laplace transformations.

Learning calculus can be daunting, but don't feel intimidated by calculus - if you're at this stage, you have earned the right to be here and know that you're not going in completely unarmed. Calculus takes your knowledge of algebra, trigonometry and geometry and elevates it to a new playing field where you will continue to expand and apply these skills in new ways. Let us help you get started today!

Is calculus hard?

Calculus has a notorious reputation for being difficult. Many who fear math have poised this perception of calculus. However, there are many who excel and enjoy calculus, some more so than the likes of Algebra and Trigonometry. The reality here however is that calculus is and can be hard - but it can be dealt with.

If you are just beginning with Precalculus for dummies or even Calculus for dummies, there's no need to fret. Take your time to learn calculus essentials, familiarize yourself with calculus equations and follow along calculus examples to learn new techniques and problem solving strategies. Laying the groundwork here is important and will help you advance to more difficult calculus topics with ease. Remember that concepts are sequential and compounded on one another, so skip back if you feel like you need a quick refresher on common antiderivatives, more limits practice or a complete Calculus 1 review.

Like any other math topic, expect to face challenges. Furthermore, not all calculus problems are made equal. This is where we come in – getting the right calculus help will make a difference like night and day. Say goodbye to the repetitive monotony of calculus worksheets and join us for a real immersive, interactive and fun learning experience! At StudyPug we offer over 1000's of lessons, all brief yet comprehensive to help you tackle even the most arduous calculus questions.

Learn the lessons but don't stop there – journey with us as we dive deeper into the nitty gritty details, dissecting questions by going through step-by-step examples. Follow this up with easy practice to truly make the most out of your calculus exam prep. Our bank of 1179 questions is unrivalled by any, covering anything and everything under the sun! Let us supply you with all the practice and insight on the kinds of questions you can expect on your homework or upcoming test. Lastly, with our 24/7 help, never lose a night of sleep or throw a tantrum again. No more wasted time searching for a tutor, waiting for tutors to come online or commuting to a tutor – get calculus help now!

How to learn calculus?

When it comes to calculus, or any math subject, students are quick to ask "how to do calculus" instead of seeking "How to learn calculus". In this modern day and age, to learn calculus online is quickly becoming the norm, whether it is for College Calculus or Calculus for beginners. With the advancement in technology and increase in accessibility of online resources, StudyPug aims to provide a superior service for those looking to learn calculus online, a calculus refresher, or access online calculus review material.

Learning calculus online begins with calculus videos. Unlike conventional math lessons, here at StudyPug, we've condensed our lessons to be short, sweet, digestible and engaging. Give us 5-10 minutes of your time, and we'll clear up confusions, and lay down solid foundations. We've also dedicated a large portion of our lessons to walk you through examples – learn the steps, how to avoid common pitfalls and master tricks and new techniques. Rest assured, our knowledgeable calculus tutors will help you lay your fears and qualms to rest. Still feeling lost? We'll take you back as far as Precalculus or Algebra if necessary!

Looking for something more to chew on like our resident StudyPugs? Take a gander at our articles below each video lesson. These articles are your personal online notes where we break down calculus formulas, provide more calculus review, go over examples and frequently asked questions.

No learning is complete without actually testing your understanding. Go through as many calculus practice problems as you can to see how helpful our lessons were and how well you understood the concepts. Produce the confidence and sharpen the skills you need for that upcoming calculus test! If there is a calculus problem that escapes you, quickly backtrack to our walk-through examples or rewatch the lesson in no time.

What textbooks do we use here at StudyPug?

Choosing the best calculus textbook to use will be the least of your worries here at StudyPug. Our help page covers calculus content found in textbooks like Calculus: Early Transcendentals, Springer Calculus II, Pearson Calculus, Calculus for dummies pdf, and many more! Keep calm and carry on with our Calculus help knowing that any calculus book or calculus textbook pdf you may be using will still be relevant and perhaps even more helpful once you've used StudyPug! Never be put down by a mind-boggling calculus problem from your textbook again!

Feeling like you need more practice with differentiation calculus? Still stressed out with calculus integrals? Get into shape with our exercises and kick-start your success! With over 1000 calculus practice problems, be prepared for every style and level of calculus questions!