Parallel and perpendicular line segments
Topic Notes
In this lesson, we will learn:
- How to measure and draw angles using a protractor
- How to identify whether pairs of lines or line segments are parallel or perpendicular
Notes:
- Protractors are used for measuring and drawing angles:
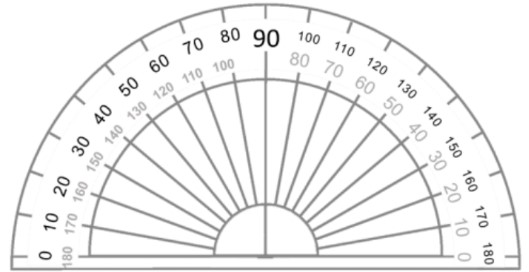
- The middle of the flat side of the protractor goes on the vertex of the angle
- There are two scales on the protractor from 0° to 180° (one going the clockwise way, one going the counter-clockwise way)
- Line up one of the zeroes on the protractor with one arm of the angle and start measuring from 0° until you reach the other arm
- Two lines or line segments can either intersect (cross) each other or be parallel. In this section, we will be learning how to identify and draw parallel and perpendicular line segments. Parallel line segments never meet, no matter how far they are extended. Two line segments are perpendicular if they form a 90 degree angle where they cross. Parallel and perpendicular line segments are found everywhere in the world around us. For example, city planners often design roads to be parallel and perpendicular to each other. Along with roads, railroad tracks, lines on notebook paper, and bookcases are parallel.
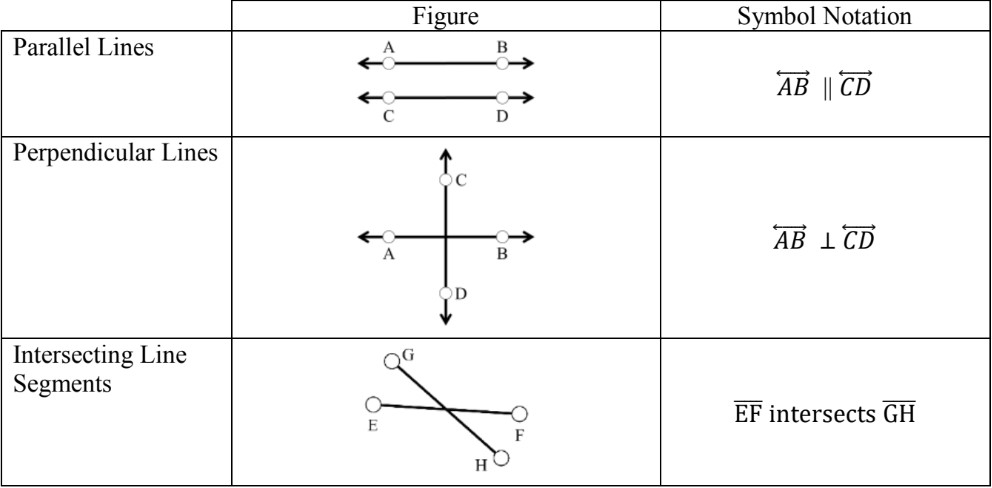
- When two figures are parallel with each other we can use the symbol:
- When two figures are perpendicular with each other we can use the symbol:
Introduction to Parallel and Perpendicular Line Segments
Welcome to our exploration of parallel and perpendicular line segments! These fundamental concepts are crucial in geometry and have real-world applications. Parallel line segments never intersect and maintain a constant distance between them, like railroad tracks. On the other hand, perpendicular line segments meet at a right angle (90 degrees), forming an "L" shape. Our introduction video provides a visual demonstration of these concepts, making them easier to grasp. You'll see how parallel vs perpendicular line segments differ and how they relate to various shapes and structures. Understanding these concepts is essential for solving more complex geometric problems. As we dive deeper, you'll discover how these line segments form the basis of many geometric figures and architectural designs. Whether you're studying for a test or simply curious about geometry, mastering parallel and perpendicular line segments will give you a solid foundation in spatial reasoning.
Parallel line segments are often used in various engineering and architectural designs due to their stability and uniformity. In contrast, right angle intersections are crucial in construction for creating strong and stable structures. By understanding the principles of parallel and perpendicular lines, you can enhance your geometric problem-solving skills and apply them to real-world scenarios.
Understanding Line Segments
Line segments are an important concept in geometry that students often encounter. But what exactly are line segments, and how do they differ from lines? Let's explore this topic and look at some line segment examples to help you understand better.
A line segment is a part of a line that has two definite endpoints. Unlike a line, which extends infinitely in both directions, a line segment has a specific beginning and end. Imagine drawing a straight line on a piece of paper and then marking two points on it - the part of the line between those two points is a line segment.
So, what does a line segment look like? Picture a straight pencil or a ruler - these are real-life examples of line segments. In geometric drawings, a line segment is typically represented by a straight line with two clearly marked endpoints, often labeled with letters.
When it comes to how to write a line segment in mathematical notation, we use uppercase letters to denote the endpoints. For example, if we have a line segment with endpoints A and B, we write it as AB or BA. The order of the letters doesn't matter, as AB and BA represent the same line segment.
Let's look at some more line segments examples:
- The edge of a table
- A stick
- The side of a rectangle
- A line drawn between two stars on a map
In geometry, you might see problems asking you to measure or compare line segments. For instance, you could be asked to find the length of line segment PQ or determine if line segment XY is longer than line segment MN.
It's important to remember that while a line segment has a definite length, a line does not. If you were to measure a line segment, you could give it a specific measurement, like 5 centimeters or 3 inches. However, you can't measure the length of a line because it goes on forever in both directions.
Understanding line segments is crucial for more advanced geometric concepts. They form the basis for many shapes and figures, such as triangles, squares, and polygons. By grasping the concept of line segments, you're building a strong foundation for future math learning.
Remember, whenever you see two points connected by a straight path with clear endpoints, you're looking at a line segment. Practice identifying line segments in your everyday life - from the legs of a chair to the lines on a basketball court - and you'll soon become an expert at recognizing and working with these fundamental geometric elements.
Parallel Line Segments
Parallel line segments are an essential concept in geometry that we encounter both in mathematics and everyday life. But what exactly are parallel line segments, and how can we identify them? Let's dive into this fascinating topic and explore its properties, examples, and applications.
Parallel line segments are two or more line segments that maintain a constant distance from each other throughout their length. In other words, if you were to extend these segments infinitely in both directions, they would never intersect. This property is what defines parallel line segments and sets them apart from other geometric relationships.
So, how do you know if two line segments are parallel? There are several ways to determine this:
- Equal angles: If two line segments form equal corresponding angles when intersected by a transversal line, they are parallel.
- Perpendicular to the same line: If two line segments are both perpendicular to the same line, they are parallel to each other.
- Slope: In coordinate geometry, line segments with the same slope are parallel.
The notation for parallel line segments is typically represented by two vertical bars (||). For example, if we have two line segments AB and CD that are parallel, we would write AB || CD.
But which way is parallel, and what does parallel look like? Imagine two straight lines that never meet, no matter how far you extend them. That's what parallel looks like. In real life examples of parallel lines, we see examples of parallel line segments all around us:
- Railroad tracks
- Opposite sides of a rectangle or parallelogram
- Lines on ruled paper
- Edges of a table or desk
- Lanes on a highway
In mathematics, parallel line segments play a crucial role in various geometric concepts and proofs. They are fundamental in understanding shapes like parallelograms, rectangles, and squares. Parallel segments also help in solving problems related to distance, area, and angle measurements.
One interesting property of parallel line segments is that any line perpendicular to the same line will also be perpendicular to the other. This property is often used in construction and engineering to ensure structures are built with proper alignment.
Another important aspect of parallel line segments is their behavior when intersected by a transversal line. This intersection creates corresponding angles, alternate angles, and co-interior angles, all of which have special properties that are useful in geometric proofs and problem-solving.
Understanding parallel line segments is not just about recognizing them visually. It's about grasping the underlying principles that make them parallel. This knowledge is invaluable in fields such as architecture, engineering, and computer graphics, where precise spatial relationships are crucial.
In conclusion, parallel line segments are a fundamental concept in geometry with wide-ranging applications. Whether you're solving a math problem, designing a building, or simply observing the world around you, the ability to identify and understand parallel segments is a valuable skill. By recognizing the properties and notation of parallel line segments, you'll be better equipped to tackle geometric challenges and appreciate the mathematical precision in everyday objects.
Perpendicular Line Segments
Perpendicular line segments are a fundamental concept in geometry that plays a crucial role in various mathematical applications and everyday life. To understand perpendicular line segments, let's start with their definition. Two line segments are considered perpendicular when they intersect at a right angle (90 degrees). This means that when these segments meet, they form a perfect L-shape.
The properties of perpendicular line segments are essential to recognize. When two lines or line segments are perpendicular, they create four congruent angles at their point of intersection. Each of these angles measures exactly 90 degrees. This property is what gives perpendicular lines their distinctive appearance and makes them so useful in various applications.
You might wonder, "How do you know if two line segments are perpendicular?" There are several ways to identify perpendicular segments. One method is to use a protractor to measure the angle between the segments. If it's 90 degrees, they're perpendicular. Another way is to use the slopes of the lines containing the segments. If the product of their slopes is -1, the lines (and consequently, the segments) are perpendicular.
In mathematics, we use a special notation to indicate perpendicular line segments. The symbol "" is used to denote perpendicularity. For example, if line segment AB is perpendicular to line segment CD, we write it as AB CD. This concise notation is widely used in geometric proofs and descriptions.
Perpendicular line segments are not just abstract mathematical concepts; they're all around us in everyday life. Some common examples include:
- The corner of a room where walls meet the floor
- The intersection of streets in a grid-like city layout
- The hands of an analog clock at 3:00
- The edges of a sheet of paper
- The crossbars on a soccer goal post
In mathematics, perpendicular line segments are crucial in various areas. They're used in constructing geometric shapes, solving problems in trigonometry, and are fundamental in coordinate geometry. For instance, in the Cartesian coordinate system, the x and y axes are perpendicular to each other, forming the basis for plotting points and graphing functions.
Understanding what a perpendicular line is and recognizing perpendicular line examples can greatly enhance your spatial reasoning and problem-solving skills. In architecture and engineering, perpendicular lines ensure structural stability and aesthetic balance. In art and design, they create a sense of order and can be used to draw the viewer's attention to specific elements.
To further illustrate the concept, imagine a capital letter "T". The vertical and horizontal lines in this letter are perfect examples of perpendicular line segments. This simple visualization can help you quickly identify perpendicularity in various contexts.
In conclusion, perpendicular line segments are a fascinating and essential aspect of geometry with wide-ranging applications. From the precise angles in building construction to the clean lines in graphic design, perpendicular segments contribute to the structure and beauty of our world. By understanding and recognizing these geometric elements, you'll gain a deeper appreciation for the mathematics that shapes our environment and enhances our problem-solving capabilities.
Comparing Parallel and Perpendicular Line Segments
When exploring geometry, understanding the difference between parallel and perpendicular line segments is crucial. These two concepts are fundamental in various mathematical applications and real-world scenarios. Let's dive into the world of parallel versus perpendicular lines and uncover their unique characteristics.
Parallel line segments are two or more lines that never intersect, no matter how far they extend. They maintain a constant distance between them throughout their length. Imagine railroad tracks or the opposite sides of a rectangle - these are perfect examples of parallel lines. On the other hand, perpendicular line segments intersect at a right angle (90 degrees). Picture the corner of a square or the hands of a clock at 3:00 - these demonstrate perpendicular lines.
The key difference between perpendicular and parallel lines lies in their relationship to each other. Parallel lines never meet and always maintain the same distance, while perpendicular lines intersect at exactly one point, forming a right angle. This distinction is crucial in various fields, from architecture to engineering.
So, what is parallel and perpendicular in practical terms? Parallel lines are often found in everyday objects like notebook paper, window blinds, or the stripes on a zebra. Real-world examples of perpendicular lines are commonly seen in the corners of rooms, the intersection of streets in a grid system, or the hands of an analog clock at certain times.
Determining if two line segments are parallel or perpendicular involves examining their slopes. Parallel lines have the same slope, while the slopes of perpendicular lines are negative reciprocals of each other. For instance, if one line has a slope of 2, its perpendicular line would have a slope of -1/2.
When asked how lines KL and MN are related, we need to consider their slopes and positions. If their slopes are identical, they're parallel. If their slopes are negative reciprocals, they're perpendicular. If neither condition is met, the lines are neither parallel nor perpendicular.
Understanding these concepts is essential in various fields. Architects use parallel and perpendicular lines to design structurally sound buildings. Engineers rely on these principles when creating machinery and infrastructure. Even in art and design, the interplay between parallel and perpendicular elements can create visually striking compositions.
In conclusion, while parallel and perpendicular line segments may seem like simple geometric concepts, they play a vital role in shaping our world. From the buildings we inhabit to the roads we travel, these fundamental principles of geometry are all around us, silently influencing our daily lives and the structures that surround us. Real-world examples of perpendicular lines are everywhere, demonstrating the importance of these geometric principles.
Real-World Applications of Parallel and Perpendicular Line Segments
Parallel and perpendicular line segments are fundamental geometric concepts that have numerous real-world applications across various fields. Understanding these concepts can greatly enhance problem-solving skills and design capabilities in architecture, engineering, art, and everyday life.
In architecture, parallel line segments are frequently used in building design. For example, the walls of a room are often parallel to each other, creating a structured and balanced space. Similarly, floor joists and roof trusses are typically installed as parallel line segments to ensure even weight distribution and structural integrity. Perpendicular line segments are equally important in architectural design, as they form right angles essential for creating stable corners and intersections between walls, floors, and ceilings.
Engineering relies heavily on both parallel and perpendicular line segments. In road construction, highway lanes are designed as parallel line segments to maintain consistent traffic flow and safety. Bridge design often incorporates parallel support beams to distribute weight evenly across the structure. Perpendicular line segments are crucial in electrical engineering, where circuit boards are designed with components arranged at right angles to optimize space and minimize interference.
The world of art also embraces these geometric concepts. Many artists use parallel line segments to create depth and perspective in their paintings or drawings. Two line segments that are parallel to each other can guide the viewer's eye and create a sense of order and balance in a composition. Perpendicular line segments are often employed to create strong visual contrasts and dynamic compositions, as seen in the works of artists like Piet Mondrian.
In everyday life, we encounter parallel and perpendicular line segments more often than we might realize. The shelves in a bookcase are typically parallel to each other, allowing for efficient storage and organization. The edges of a table or desk often form perpendicular line segments, creating a stable and functional surface. Even in sports, the boundaries of a tennis court or football field are marked by parallel and perpendicular line segments to define the playing area.
Understanding these concepts can significantly enhance problem-solving skills in various scenarios. For instance, when arranging furniture in a room, considering parallel and perpendicular relationships can help optimize space and create a harmonious layout. In DIY projects, recognizing when two line segments should be parallel or perpendicular is crucial for achieving precise and professional-looking results.
In the field of graphic design, parallel and perpendicular line segments play a vital role in creating visually appealing layouts. Designers often use grids based on these geometric principles to align text and images, resulting in clean and organized designs. Similarly, in web design, understanding how to use parallel and perpendicular elements can lead to more intuitive and user-friendly interfaces.
The concept of parallel line segments is also essential in manufacturing and production lines. Conveyor belts and assembly lines are designed with parallel paths to ensure smooth and efficient movement of materials or products. In agriculture, crop rows are often planted in parallel lines to facilitate irrigation and harvesting processes.
Perpendicular line segments are particularly important in construction and carpentry. When framing a house or building furniture, ensuring that joints and corners are perpendicular is crucial for structural integrity and aesthetic appeal. Two line segments that are perpendicular to each other form the basis of many measuring and layout tools, such as T-squares and framing squares, which are indispensable in these trades.
In conclusion, the applications of parallel and perpendicular line segments are vast and varied. From the grand scale of architectural marvels to the minute details of electronic circuits, these geometric concepts shape the world around us. By recognizing and understanding the relationships between parallel and perpendicular line segments, we can approach design challenges and problem-solving tasks with greater confidence and creativity. Whether you're an architect, engineer, artist, or simply someone looking to optimize your living space, the principles of parallel and perpendicular line segments offer valuable insights and practical solutions for everyday challenges.
Practice Problems and Solutions
Let's dive into some practice problems to help you master parallel and perpendicular line segments. We'll work through these step-by-step, just like we're sitting together for a tutoring session. Don't worry if you find some challenging that's how we learn and grow!
Problem 1: Identifying Parallel Segments
Given the following coordinates, determine which pairs of line segments are parallel:
- AB: (1,2) to (4,5)
- CD: (0,1) to (3,4)
- EF: (-1,3) to (2,6)
Solution: To determine if line segments are parallel, we need to compare their slopes. Let's calculate them:
- AB slope: (5-2)/(4-1) = 3/3 = 1
- CD slope: (4-1)/(3-0) = 3/3 = 1
- EF slope: (6-3)/(2-(-1)) = 3/3 = 1
All three line segments have the same slope of 1, so they are all parallel to each other!
Problem 2: Finding a Perpendicular Segment
Given the line segment from (0,0) to (3,6), find the equation of a line perpendicular to this segment that passes through the point (2,1).
Solution: Let's break this down:
- Find the slope of the given line segment: (6-0)/(3-0) = 2
- The perpendicular line will have a slope that's the negative reciprocal: -1/2
- Use point-slope form with (2,1) and slope -1/2: y - 1 = (-1/2)(x - 2)
- Simplify to get: y = -1/2x + 2
Great job! The perpendicular line's equation is y = -1/2x + 2.
Problem 3: Proving Segments are Perpendicular
Prove that the line segments AB and CD are perpendicular:
- A(1,1), B(4,7)
- C(2,8), D(5,2)
Solution: To prove perpendicularity, we'll show that the product of their slopes is -1:
- Slope of AB: (7-1)/(4-1) = 6/3 = 2
- Slope of CD: (2-8)/(5-2) = -6/3 = -2
- Product of slopes: 2 * (-2) = -4
The product isn't -1, so these segments are not perpendicular. Don't worry if you thought they might be this is a great learning opportunity!
Problem 4: Constructing a Parallel Segment
Given the line segment from (1,2) to (4,8), find the coordinates of a parallel segment of the same length starting at the point (0,0).
Solution: Let's approach this step-by-step:
- Calculate the slope: (8-2)/(4-1) = 6/3 = 2
- Find the length: ((4-1)² + (8-2)²) = (
Conclusion
Understanding parallel and perpendicular line segments is crucial in geometry. Parallel lines never intersect and maintain a constant distance, while perpendicular lines intersect at right angles. The introduction video we've explored provides a solid foundation for grasping these concepts. Remember, parallel lines have the same slope, whereas perpendicular lines intersect at right angles and have slopes that are negative reciprocals of each other. This knowledge is essential for solving various geometric problems and understanding more complex shapes. To reinforce your learning, try practicing more problems involving parallel vs perpendicular line segments. You can also explore related topics like angles formed by intersecting lines or properties of polygons. Don't hesitate to revisit the video if you need a refresher. Keep up the great work in your geometry journey! The more you practice, the more confident you'll become in distinguishing between parallel and perpendicular line segments. Happy learning!
Example:
Below is a line segment, AB.
Draw a line segment that is perpendicular to AB.

Step 1: Understanding Perpendicular Lines
To draw a line segment that is perpendicular to AB, we first need to understand what perpendicular lines are. Perpendicular lines are two lines that intersect at a 90-degree angle. A common example of perpendicular lines is the letter "T," where the top horizontal line and the vertical line meet at a right angle.
Step 2: Visualizing the Perpendicular Line
Imagine the letter "T" where the top horizontal line represents the line segment AB. The vertical line of the "T" will be the perpendicular line we need to draw. This visualization helps us understand that the perpendicular line will intersect AB at a 90-degree angle.
Step 3: Using a Protractor
To draw the perpendicular line accurately, we will use a protractor. Place the protractor on the line segment AB such that the midpoint of the protractor aligns with the point where you want the perpendicular line to intersect AB. Ensure that the baseline of the protractor is aligned with AB.
Step 4: Measuring the 90-Degree Angle
With the protractor in place, locate the 90-degree mark on the protractor. This mark indicates the direction in which the perpendicular line will be drawn. Make a small mark on the paper at the 90-degree point to guide your drawing.
Step 5: Drawing the Perpendicular Line
Using a ruler, draw a straight line from the point where the protractor's midpoint was placed through the 90-degree mark you made. This line will be perpendicular to AB, forming a 90-degree angle at the intersection point.
Step 6: Verifying the Perpendicularity
To ensure that the line you drew is indeed perpendicular to AB, you can use the protractor again. Place the protractor back on AB and check that the angle between AB and the new line is exactly 90 degrees. This verification step confirms that the lines are perpendicular.
Step 7: Understanding the Geometry
It's important to understand why the perpendicular line forms a 90-degree angle. A straight line measures 180 degrees. When a line is divided into two equal parts by a perpendicular line, each part measures 90 degrees. Therefore, the perpendicular line creates two 90-degree angles, confirming its perpendicularity.
Step 8: Finalizing the Drawing
Once you have verified the perpendicularity, you can finalize your drawing by darkening the perpendicular line. Label the new line segment appropriately to indicate that it is perpendicular to AB. This completes the task of drawing a perpendicular line segment to AB.
FAQs
Here are some frequently asked questions about parallel and perpendicular line segments:
1. What is the difference between perpendicular and parallel lines?
Parallel lines are two or more lines that never intersect and maintain a constant distance between them. Perpendicular lines, on the other hand, intersect at a right angle (90 degrees). Parallel lines have the same slope, while perpendicular lines have slopes that are negative reciprocals of each other.
2. How do you find if a line is perpendicular or parallel?
To determine if lines are parallel or perpendicular, compare their slopes:
- Parallel lines: Have the same slope (m1 = m2)
- Perpendicular lines: Have slopes that are negative reciprocals of each other (m1 * m2 = -1)
If you have equations in the form y = mx + b, compare the m values. For point-slope form, calculate the slopes using (y2 - y1) / (x2 - x1).
3. What are some examples of parallel and perpendicular lines in real life?
Parallel lines examples:
- Railroad tracks
- Opposite sides of a rectangle
- Lines on ruled paper
Perpendicular lines examples:
- The corner where two walls meet
- The hands of a clock at 3:00
- The edges of a sheet of paper
4. How do you write a perpendicular line segment?
To denote that line segment AB is perpendicular to line segment CD, you would write: AB CD. The "" symbol represents perpendicularity in geometry.
5. What is a line segment and how is it different from a line?
A line segment is a part of a line with two definite endpoints. It has a specific length and is denoted by the letters of its endpoints (e.g., AB). A line, in contrast, extends infinitely in both directions and has no endpoints or defined length.
Prerequisite Topics
Understanding parallel and perpendicular line segments is a crucial concept in geometry and algebra. However, to fully grasp this topic, it's essential to have a solid foundation in certain prerequisite concepts. Two key areas that significantly contribute to comprehending parallel and perpendicular lines are trigonometry and linear functions.
One important prerequisite is the ability to use tangent ratio to calculate angles and sides. This concept, often associated with the tangent ratio formula (Tan = opposite / adjacent), is fundamental in understanding the relationships between angles and sides in right triangles. The right angle definition is particularly relevant when dealing with perpendicular lines, as these lines intersect at right angles (90 degrees).
Another crucial prerequisite is graphing from slope-intercept form y=mx+b. This skill is essential for visualizing and analyzing linear functions, which directly relates to understanding parallel and perpendicular lines. The slope (m) in the slope-intercept form plays a vital role in determining whether lines are parallel or perpendicular. Parallel lines have the same slope, while perpendicular lines have slopes that are negative reciprocals of each other.
The point-slope form equation is another important concept that builds upon the slope-intercept form. It provides a different perspective on linear equations and can be particularly useful when working with parallel and perpendicular lines, especially when given a point and a slope.
By mastering these prerequisite topics, students can develop a stronger foundation for understanding parallel and perpendicular line segments. The tangent ratio helps in comprehending the angular relationships, particularly in right triangles formed by perpendicular lines. Meanwhile, graphing linear functions and understanding different equation forms provide the necessary skills to analyze and compare the slopes of lines, which is crucial for identifying parallel and perpendicular relationships.
Moreover, these prerequisites offer practical applications beyond just theoretical knowledge. In real-world scenarios, such as architecture, engineering, and design, the ability to work with parallel and perpendicular lines is invaluable. Understanding the underlying concepts of trigonometry and linear functions enhances problem-solving skills and spatial reasoning, which are essential in these fields.
In conclusion, a solid grasp of these prerequisite topics not only facilitates a deeper understanding of parallel and perpendicular line segments but also provides a broader perspective on how these concepts interconnect within mathematics. This comprehensive approach to learning ensures that students are well-equipped to tackle more advanced geometric and algebraic concepts in their future studies.

