Area and perimeter of rectangles
Topic Notes
In this lesson, we will learn:
- The basic properties of the shape of the rectangle
- How to understand and calculate the perimeter of a rectangle
- How to understand and calculate the area of a rectangle
Notes:
- A rectangle is a 2D (two-dimensional) shape with 4 straight sides and 4 right angles (90°)
- Each pair of sides (across from each other) are the exact same length
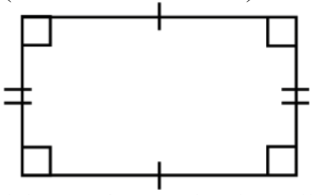
- A square is a special type of rectangle where all side lengths are the same

- The perimeter is the exact distance around the shape.
- Perimeter is a 1D (one-dimensional) quantity
- It uses units such as meters (m, cm, mm, km), miles (mi), yards (yd), or inches and feet (in and ft)
- For rectangles, the formula is written as:
- Prectangle =
- Where is length, and w is width
- For squares, the formula is written as:
- Prectangle =
- Where is side length
- The area is the space that is covered by the shape.
- Area is a 2D (two-dimensional) quantity
- It uses squared units such as square meters (m2, cm2, mm2, km2), square miles (mi2), square yards (yd2), or square inches and feet (in2 and ft2)
- For rectangles, the formula is written as:
- Arectangle =
- Where is length, and w is width
- For squares, the formula is written as:
- Asquare =
- Where is side length
Introduction to Area and Perimeter of Rectangles
Welcome to our exploration of area and perimeter of rectangles! These fundamental concepts are essential in geometry and have practical applications in everyday life. Our introduction video serves as a perfect starting point, offering a clear and engaging overview of these important ideas. The video breaks down the definitions of area (the space inside a shape) and perimeter (the distance around a shape) in simple terms. You'll learn how to calculate perimeter of rectangles using easy-to-follow formulas. Understanding these concepts is crucial for advancing in geometry and solving real-world problems. Whether you're measuring a room for new flooring or calculating fencing needed for a garden, these skills are invaluable. The video also demonstrates how relationship between area and perimeter relate to each other, providing a solid foundation for more complex geometric concepts. Let's dive in and discover the fascinating world of rectangles!
Our introduction video serves as a perfect starting point, offering a clear and engaging overview of these important ideas. The video breaks down the definitions of area (the space inside a shape) and perimeter (the distance around a shape) in simple terms. You'll learn how to calculate perimeter of rectangles using easy-to-follow formulas. Understanding these concepts is crucial for advancing in geometry and solving real-world problems. Whether you're measuring a room for new flooring or calculating fencing needed for a garden, these skills are invaluable. The video also demonstrates how relationship between area and perimeter relate to each other, providing a solid foundation for more complex geometric concepts. Let's dive in and discover the fascinating world of rectangles!
Understanding Rectangles
Rectangles are fascinating shapes that we encounter every day, from the pages of a book to the screens of our devices. Let's dive into the world of rectangles and explore what makes them unique! First, it's important to understand that a rectangle is a 2D shape, which means it has length and width but no depth. It's flat, like a piece of paper.
A rectangle is also classified as a polygon, which is a closed shape with straight sides. Specifically, a rectangle has four sides and four corners. But what really sets rectangles apart is that all four of its angles are right angles. Remember those 90-degree angles from math class? That's what we're talking about!
Now, let's break down the key properties of rectangles:
- Four sides: Two pairs of parallel sides
- Four right angles: Each corner is 90 degrees
- Opposite sides are equal in length
- Diagonals bisect each other
Here's a fun fact: all squares are rectangles, but not all rectangles are squares! Squares are special rectangles where all four sides are equal in length. Think of it like this: a square is like a rectangle that decided to make all its sides the same size.
To help visualize this, imagine a door. Most doors are rectangular, with two longer sides (height) and two shorter sides (width). Now, picture a perfectly square window it's still a rectangle, but all sides are the same length.
Rectangles are incredibly common in our world. Look around you how many can you spot? From picture frames to smartphone screens, rectangles are everywhere. Their simple yet versatile shape makes them ideal for countless applications in design, architecture, and everyday objects.
Understanding rectangles is a great starting point for exploring more complex shapes. As you continue your journey in geometry, remember that these basic 2D shapes form the foundation for more advanced concepts. So the next time you see a rectangle, take a moment to appreciate its perfect right angles and opposite sides equal length it's a small but significant part of the geometric world around us!
Dimensions and Perimeter
Let's dive into the fascinating world of geometry! Today, we're going to explore dimensions and perimeter, focusing on rectangles and squares. Don't worry if these terms sound a bit intimidating I'll guide you through each concept step by step.
First, let's talk about dimensions. In geometry, dimensions refer to the measurable aspects of an object, like its length, width, or height. For flat shapes like rectangles, we usually deal with two dimensions: length and width.
Now, let's introduce the concept of perimeter. Imagine you're walking around the edge of a field. The total distance you'd travel to go all the way around is the perimeter. It's like tracing the outline of a shape with your finger.
For rectangles, calculating the perimeter is pretty straightforward. You just need to add up the lengths of all four sides. Since opposite sides of a rectangle are equal, we can use this simple formula:
Perimeter formula for rectangles = 2 × (length + width)
Let's break this down with an example. Suppose we have a rectangle that's 5 meters long and 3 meters wide. To find the perimeter, we'd do:
Perimeter = 2 × (5 + 3) = 2 × 8 = 16 meters
See? It's not so tricky! You're basically saying, "I need to go 5 meters, then 3 meters, then 5 meters again, and finally 3 meters to get back where I started." Add those up, and you get 16 meters.
Now, what about squares? Well, squares are special rectangles where all sides are equal. This makes our perimeter calculation even easier! If we know the length of one side, we can find the perimeter by multiplying it by 4:
Perimeter of a square = 4 × side length
Let's try an example. If we have a square with sides 4 centimeters long, the perimeter would be:
Perimeter = 4 × 4 = 16 centimeters
Easy, right? You're getting the hang of this!
Here's a fun way to remember: think of perimeter as the "distance around." Whether it's a rectangle or a square, you're just finding out how far you'd walk if you traced the shape's outline.
Now, let's practice with one more example. Imagine you have a rectangular garden that's 8 feet long and 6 feet wide. How much fencing would you need to go all the way around it?
Let's use our formula: Perimeter formula for rectangles
Plugging in our numbers: Perimeter = 2 × (8 + 6) = 2 × 14 = 28 feet
So, you'd need 28 feet of fencing to enclose your garden completely.
Remember, calculating perimeter is all about adding up the lengths of all sides. For rectangles, we can shortcut this by doubling the sum of the length and width. For squares, it's even simpler just multiply one side length by 4.
As you practice more, you'll find that calculating perimeters becomes second nature. It's a valuable skill that comes in handy in many real-life situations, from gardening to home improvement projects. Keep exploring, and don't hesitate to ask questions. Geometry can be fun when you approach it step by step!
Understanding Area
Area is a fundamental concept in geometry that measures the amount of space occupied by a two-dimensional shape. It's an essential measurement in various fields, from architecture and engineering to everyday life situations like calculating the size of a room or a garden plot. Understanding area helps us comprehend the size and scale of objects and spaces around us.
To grasp the concept of area, let's introduce the idea of unit squares. A unit square is a square with sides measuring one unit in length. These unit squares serve as the building blocks for measuring area. Imagine covering a flat surface with these unit squares the number of squares needed to cover the surface completely represents its area.
This is why area measurement in squared units. When we say "square meters" or "square feet," we're referring to the number of unit squares (each measuring one meter or one foot on each side) that would fit within the shape. For example, an area of 9 square meters means that 9 squares, each measuring 1 meter by 1 meter, would cover the surface entirely.
The use of squared units in area measurement in squared units stems from the two-dimensional nature of the shapes we're measuring. Since we're dealing with length and width, we multiply these two dimensions, resulting in a squared unit. This is different from linear measurements like length, which use simple units like meters or feet.
For rectangles and squares, calculating area is straightforward. The area formula for rectangles is:
Area = Length × Width
For a square, since all sides are equal, the formula simplifies to:
Area = Side × Side or Area = Side²
Let's look at some examples to illustrate these concepts:
1. Rectangle: If you have a rectangular room that is 5 meters long and 4 meters wide, its area would be:
Area = 5 m × 4 m = 20 square meters (m²)
2. Square: For a square garden plot with sides measuring 6 meters, the area would be:
Area = 6 m × 6 m = 36 square meters (m²)
Visualizing these calculations can be helpful. Imagine drawing a grid on the rectangle or square, where each cell represents one unit square. For the rectangular room, you'd have 5 rows of 4 squares each, totaling 20 squares. For the square garden, you'd see 6 rows of 6 squares, adding up to 36 squares.
Understanding area becomes even more important when dealing with more complex shapes. While circles, triangles, and irregular shapes require different formulas, the basic principle of counting or calculating the number of unit squares that fit within the shape remains the same.
As you continue to explore the concept of area, remember that it's a practical and useful tool in many aspects of life. Whether you're planning to paint a wall, install flooring, or create a scale model, your understanding of area will prove invaluable. Don't be discouraged if it takes some time to fully grasp practice and real-world applications will help solidify your understanding.
Keep in mind that area calculations can extend to three-dimensional objects as well, where you might need to calculate the surface area. This concept builds upon your understanding of two-dimensional area and applies it to the faces of 3D shapes.
As you progress in your geometry studies, you'll discover how area relates to other mathematical concepts and how it forms the foundation for more advanced topics. Embrace each new challenge as an opportunity to deepen your understanding and appreciation of the mathematical principles that shape our world.
Practical Applications
Area and perimeter calculations for rectangles might seem like abstract math concepts, but they have numerous real-world applications that we encounter in our everyday lives. Let's explore some practical uses of these calculations and see how they can be incredibly useful in various situations.
One common application is in home improvement and interior design. When you're planning to redecorate a room, knowing how to calculate the area of a rectangular floor space is essential. This skill helps you determine how much carpeting, hardwood flooring, or tiles you'll need to cover the entire room. Similarly, if you're thinking about painting your walls, calculating the perimeter of the room will give you an idea of how much paint you'll need to purchase.
Gardening and landscaping enthusiasts often use these calculations too. If you're planning to fence your backyard, you'll need to know the perimeter of the area to determine how much fencing material to buy. For those creating raised garden beds or planning a new lawn, area calculations come in handy for figuring out how much soil, mulch, or grass seed you'll need.
In the world of real estate and property management, area calculations are crucial. Realtors use floor area measurements to determine property values and rental prices. If you're a tenant, understanding how to calculate the area of your apartment can help you compare different rental options and ensure you're getting a fair deal for the space you're renting.
Construction and home renovation projects heavily rely on these calculations. Whether you're installing new kitchen countertops, laying a patio, or building a deck, knowing how to calculate area and perimeter is essential for estimating material costs and planning the project effectively.
Even in our daily routines, we unconsciously use these concepts. When you're wrapping a gift, you're essentially calculating the surface area to determine how much wrapping paper you need. If you're hanging fairy lights around your room, you're using perimeter calculations to figure out the length of lights required.
For students, understanding these practical applications can make learning more engaging and relevant. Next time you're in a store, try estimating the floor space to appreciate the size of the building. When you're at a sports field, consider how area calculations are used to mark out playing surfaces. These real-world connections can help solidify your understanding of mathematical concepts and show how they're applicable in everyday situations.
Remember, area and perimeter calculations aren't just for math class they're valuable life skills that can save you time, money, and effort in various scenarios. So, the next time you encounter a rectangular space in your daily life, take a moment to think about how you might apply these calculations. You'll be surprised at how often these skills come in handy!
Common Mistakes and Tips
Calculating the area and perimeter of rectangles is a fundamental skill in geometry, but it's common for students to make mistakes. Let's address these errors and provide helpful strategies to boost your confidence in tackling these problems.
One of the most common mistakes is confusing area and perimeter formulas. Remember, area is the space inside the shape, while perimeter is the distance around it. To avoid this, try this memory aid: "A" for Area is about what's inside, while "P" for Perimeter goes around the outside.
Another frequent error is forgetting to include units in your answer. Always write your final answer with the correct units (e.g., square meters for area, meters for perimeter). A helpful tip is to circle the units in the question and carry them through your calculations.
Students often mix up length and width when applying formulas. To prevent this, clearly label your rectangle's dimensions before starting calculations. A quick sketch can be invaluable here.
When calculating perimeter, a common mistake is adding only two sides instead of all four. Remember, a rectangle has two pairs of equal sides. A memory trick is to think "PLWLW" - Perimeter equals Length plus Width plus Length plus Width.
For area calculations, multiplying incorrectly or forgetting to multiply altogether is a frequent error. The phrase "Area is LxW, don't be slow!" can help you remember to multiply length by width.
Some students struggle with unit conversions in geometry when dimensions are given in different units. Always convert to the same unit before calculating. Practice this skill separately to build confidence.
To avoid careless errors, develop a habit of double-checking your work. Use estimation to see if your answer makes sense - is the area larger than the perimeter as it should be for most rectangles?
Remember, practice makes perfect. The more problems you solve, the more familiar you'll become with these concepts. Don't be discouraged by mistakes; they're opportunities to learn and improve.
Lastly, visualize real-world examples to make these concepts more concrete. Think of a rectangular room or a book cover. Understanding how these formulas apply to everyday objects can deepen your comprehension and make the math more meaningful.
With these tips and strategies, you're well-equipped to tackle practice geometry problems confidently. Remember, every great mathematician started where you are now. Keep practicing, stay positive, and watch your skills grow!
Practice Problems: Area and Perimeter of Rectangles
Ready to put your knowledge of rectangles to the test? Let's dive into some exciting rectangle practice problems! Remember, try to solve these on your own before peeking at the solutions. You've got this!
-
Problem: Calculate the area and perimeter of a rectangle with length 8 cm and width 5 cm.
Solution: Area = length × width = 8 × 5 = 40 cm². Perimeter = 2 × (length + width) = 2 × (8 + 5) = 26 cm.
-
Problem: A rectangular garden has a perimeter of 30 meters. If its length is 10 meters, what is its width?
Solution: Perimeter = 2 × (length + width), so 30 = 2 × (10 + width). Solve for width: width = (30 ÷ 2) - 10 = 5 meters.
-
Problem: The area of a rectangular room is 48 square feet. If its length is 8 feet, what is its width?
Solution: Area = length × width, so 48 = 8 × width. Solve for width: width = 48 ÷ 8 = 6 feet.
-
Problem: A rectangular playground is 15 meters long and 10 meters wide. How much fencing is needed to surround it?
Solution: The fencing needed is equal to the perimeter. Perimeter = 2 × (length + width) = 2 × (15 + 10) = 50 meters.
-
Problem: A rectangular poster has an area of 360 cm² and a width of 12 cm. What is its length?
Solution: Area = length × width, so 360 = length × 12. Solve for length: length = 360 ÷ 12 = 30 cm.
Great job tackling these rectangle practice problems! Remember, practice makes perfect. The more you work with rectangles, the more comfortable you'll become with calculating their areas and perimeters. Don't be discouraged if you find some problems challenging that's how we learn and grow. Keep up the fantastic work!
Conclusion
In this lesson, we've explored the fundamental concepts of area and perimeter for rectangles. The introduction video provided a crucial foundation for understanding these geometric principles. Remember, area is the space inside a shape, calculated by multiplying length by width, while perimeter is the distance around the shape, found by adding all sides. These concepts are essential in various real-world applications of area and perimeter, from landscaping to architecture. We encourage you to continue practicing with different rectangle sizes and exploring more complex shapes. Try applying these concepts to real-life situations, such as calculating perimeter of rectangles for flooring needs or fencing requirements. The more you practice, the more comfortable you'll become with geometry. Don't hesitate to revisit the introduction video if you need a refresher. For further engagement, challenge yourself with irregular shapes or investigate how these principles apply in fields like engineering or design. Keep exploring, and you'll discover the fascinating world of geometry!
Introduction to Area and Perimeter of Rectangles: What are the basic properties of a rectangle?
Step 1: Understanding the Shape
In this lesson, we start by understanding what a rectangle is. A rectangle is a two-dimensional (2D) shape, meaning it is flat and has four straight sides. This differentiates it from shapes with curved sides, such as circles. Rectangles fall under the category of polygons, which are shapes with only straight sides. Other examples of polygons include triangles, pentagons, and hexagons.
Step 2: Identifying the Right Angles
One of the defining characteristics of a rectangle is that it has four right angles. Each corner of a rectangle forms a 90-degree angle. This property ensures that the opposite sides of the rectangle are parallel and equal in length. The right angles also mean that the top and bottom sides are perfectly aligned, as are the left and right sides.
Step 3: Equal Opposite Sides
Another key property of a rectangle is that its opposite sides are equal in length. This means that the top and bottom sides are the same length, and the left and right sides are also the same length. To indicate this, we often use markings on the sides. For example, a single line on the top and bottom sides shows they are equal, while a different marking on the left and right sides shows they are equal but distinct from the top and bottom sides.
Step 4: Special Case - The Square
A square is a special type of rectangle where all four sides are of equal length. This means that not only are the opposite sides equal, but all four sides are the same length. In a square, the internal angles are also right angles, making it a unique subset of rectangles. To indicate that all sides are equal, we use the same marking on all four sides.
Step 5: Dimensions and Their Importance
When discussing rectangles, it's essential to understand the concept of dimensions. Dimensions are measurements in different directions or planes. For a rectangle, we primarily consider two dimensions: length and width. These dimensions help us calculate the area and perimeter of the rectangle.
Step 6: Perimeter - The 1D Property
The perimeter of a rectangle is a one-dimensional (1D) property. It represents the total distance around the shape. To find the perimeter, we add up the lengths of all four sides. Since the opposite sides are equal, the formula for the perimeter is 2 times the length plus 2 times the width (P = 2L + 2W). The unit of measurement for the perimeter is typically in centimeters (cm) or any other unit of length.
Step 7: Area - The 2D Property
The area of a rectangle is a two-dimensional (2D) property. It represents the amount of space covered by the shape. To find the area, we multiply the length by the width (A = L × W). The unit of measurement for the area is in square centimeters (cm²) or any other unit of area. The squared unit indicates that we are measuring in two dimensions.
Step 8: Understanding 3D Shapes
While this lesson focuses on 2D shapes, it's helpful to understand that shapes can also exist in three dimensions (3D). A 3D shape, like a rectangular prism, has length, width, and height. The volume of a 3D shape is a three-dimensional property, measured in cubic units (cm³). This concept helps us understand how dimensions work in different contexts.
Conclusion
In summary, the basic properties of a rectangle include being a 2D shape with four straight sides, having four right angles, and having opposite sides that are equal in length. Understanding these properties is crucial for calculating the area and perimeter of rectangles. Additionally, recognizing the special case of squares and the concept of dimensions helps deepen our understanding of geometric shapes.
FAQs
-
What is the difference between area and perimeter?
Area is the space inside a shape, measured in square units (e.g., square meters). For rectangles, it's calculated by multiplying length by width. Perimeter is the distance around a shape, measured in linear units (e.g., meters). For rectangles, it's calculated by adding all four sides or using the formula 2 × (length + width).
-
How do I calculate the area of a rectangle?
To calculate the area of a rectangle, multiply its length by its width. The formula is: Area = length × width. For example, if a rectangle is 5 meters long and 3 meters wide, its area is 5 × 3 = 15 square meters.
-
What's the formula for the perimeter of a rectangle?
The formula for the perimeter of a rectangle is: Perimeter = 2 × (length + width). Alternatively, you can add all four sides together. For instance, if a rectangle is 6 meters long and 4 meters wide, its perimeter is 2 × (6 + 4) = 20 meters.
-
Why are area units squared?
Area units are squared because they represent two-dimensional space. When you multiply length by width, you're essentially counting the number of unit squares that fit within the shape. This results in square units like square meters (m²) or square feet (ft²).
-
How can I apply area and perimeter calculations in real life?
Area and perimeter calculations have numerous practical applications. You can use them to determine how much flooring or carpet you need for a room (area), calculate fencing required for a garden (perimeter), estimate paint needed for walls (area), or measure fabric for curtains (area). These concepts are also crucial in fields like architecture, landscaping, and construction.
Prerequisite Topics for Understanding Area and Perimeter of Rectangles
Mastering the area and perimeter of rectangles is a fundamental skill in geometry, but it requires a solid foundation in several prerequisite topics. Understanding these concepts will greatly enhance your ability to work with rectangles and apply this knowledge to real-world situations.
One crucial prerequisite is rectangles themselves. Knowing the properties of rectangles, such as their right angles and parallel sides, is essential for calculating area of rectangles accurately. This foundational knowledge helps you visualize and manipulate rectangular shapes in various problems.
Another important concept is the ability to use sine ratio to calculate angles and sides. While this may seem more advanced, understanding right angles in rectangles and their relationships to trigonometric functions can be beneficial when dealing with more complex rectangular problems or real-world applications.
When working with area and perimeter, you'll often encounter different units of measurement. That's where conversions involving squares and cubic units come into play. Being proficient in converting units in geometry ensures you can work with various measurement systems and accurately compare or combine different rectangular areas and perimeters.
Lastly, understanding complex polygons provides context for how rectangles fit into the broader world of geometric shapes. This knowledge helps in recognizing practical applications of area and perimeter in more intricate shapes that may be composed of or related to rectangles.
By mastering these prerequisite topics, you'll build a strong foundation for understanding and applying concepts related to the area and perimeter of rectangles. This knowledge will not only help you solve geometric problems more effectively but also enable you to appreciate the practical applications of these concepts in fields such as architecture, engineering, and design.
Remember, each of these prerequisite topics contributes uniquely to your overall comprehension of rectangular geometry. Taking the time to review and strengthen your understanding of these areas will significantly enhance your ability to work with rectangles and apply this knowledge in both academic and real-world contexts.

