I think we can all agree that pizza is a pretty big deal! In fact, before we get into our topic, let me drop a little knowledge on you. Did you know that the world’s largest pizza was made in 1987? It was made by Lorenzo Amato and Louis Piancone. It covered 10,000 square feet and measured 140 feet across, and as you can imagine, it wasn’t a light pizza either, weighing in at 44,457 pounds! Pretty impressive huh?

With such large quantities at play, I’m sure math played a pivotal role in the making of that pizza, which leads me nicely into our topic. Picture the scenario, You’re at a birthday party and pizza is being served, you approach the pizza and scan the box to find the “best” slice. You know the one, the slice that’s the largest and has just the right amount of toppings on it.

Unfortunately, everyone in the room has the same idea as you. you need to act fast if you want to secure that golden slice, but what if there’s another way. What if i told you that the things you’ve learnt in 6th grade math, like geometry and tessellation, have been used by mathematicians to explore the possibilities of cutting a pizza into equal sections, ensuring that each slice is identical in size.

Below are two disks (let’s call them pizzas) and each one has been divided into equal shapes. The pizza on the left shows perhaps the best way to slice a pizza into 6 equals sections. The image to the right, introduces more slices while still maintaining the equal proportions.

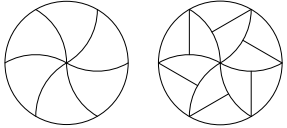Not content with that, the mathematicians wanted to see if they could go further. The mathematicians in question, were Joel Anthony Haddley and Stephen Worsley from the University of Liverpool. Together they worked on a paper entitled “Infinite Families of Monohedral Disk Tiling”.  Using their understanding of obtuse/interior angles alongside their knowledge of algebraic formulas and linear equations, they were able to successfully replicate shapes (tiling) of equal proportions into a disk (pizza).

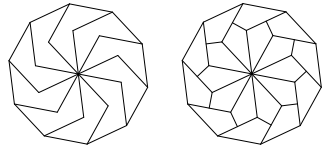As you can see from the image above, the pizza to the left  is dissected into more slices of equal amounts all of which include the crust. The second pizza however, offers a larger collection of slices and these are separated into crust and crustless. Each slice remains identical in size, offering two different slices of pizza. The middle would be rich with toppings whereas the outer slices would have the crust, making it ideal for dipping.

It’s from here that things can a little crazier.  Joel Anthony Haddley comments that “Mathematically, there is no limit whatsoever”. Meaning that the pizza could be divided even further into smaller slices of identical proportions.

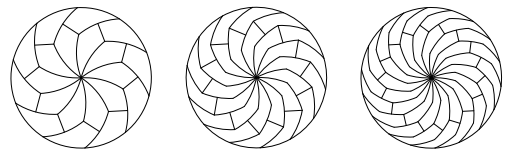
As demonstrated in the 3 disks above, you could make some rather pretty looking pizza cuts. The only issue here, is that you may be in danger of diminishing returns in relation to the amount of pizza you’re actually getting. If you were to continue breaking down the pizza into smaller and smaller slices, you would eventually end up with slices that were 100% crust! Again, If you’re into dipping, crust can go a long way, but for me, i’m all about that base…and toppings.

Now,  you can argue as much as you like when it comes to toppings. In fact, one of the largest debates in food is based around whether pineapple should be a pizza topping. In my mind, there’s no such thing as a bad pizza and now thanks to Joel Anthony Haddley and Stephen Worsley, we may no longer be bad slices either.

If you’re interested in exploring their paper, I have provided the link here. If you’d like some help understanding the topics they discuss, consider using StudyPug.

With 1000s of online video tutorials that cover a vast amount of mathematical topics including  basic algebra, trigonometry, and geometry, students the world over are learning how to use math to solve problems (much like the chefs in 1987 and our friends from the University of Liverpool).

StudyPug’s content covers all the relevant information you’d expect to find in modern math textbooks and is delivered in a conversational way that’s much easier to understand. Subscribe now and you’ll have unlimited access to every lesson on their website. Furthermore, each lesson can be paused, rewound, and fast-forwarded, ensuring that you’ll never get left behind.

Learn at your own pace and visit StudyPug today.

Credits:

Infinite families of monohedral disk tilings by Joel Anthony Haddley & Stephen Worsley

https://arxiv.org/pdf/1512.03794v1.pdf