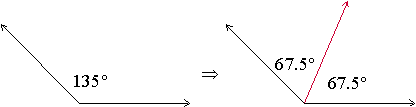As comprehensively defined by Cornell University’s Math department, Geometry is:
The visual study of shapes, sizes, patterns, and positions. It occurred in all cultures, through at least one of these five strands of human activities:
1. building/structures (building/repairing a house, laying out a garden, making a kite, …)
2. machines/motion (using a pry-bar, riding a bike, sawing a board, swinging, …)
3. navigating/star-gazing (How do I get from here to there?, using maps, …)
4. art/patterns (designs, symmetries, representations, …).
5. measurement (How big is it?, How far is it?, …)
Below is the complete resource on Geometry originally created by The Math League.
Basic Terms of Geometry
Lines
A line is one of the basic terms in geometry. We may think of a line as a “straight” line that we might draw with a ruler on a piece of paper, except that in geometry, a line extends forever in both directions.
We write the name of a line passing through two different points A and B as “line AB” or as , the two-headed arrow over AB signifying a line passing through points A and B.
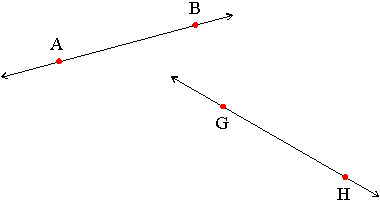
Example: The following is a diagram of two lines: line AB and line HG.
The arrows signify that the lines drawn extend indefinitely in each direction.
Points
A point is one of the basic terms in geometry. We may think of a point as a “dot” on a piece of paper. We identify this point with a number or letter. A point has no length or width, it just specifies an exact location.
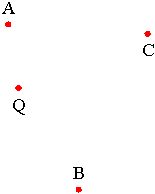
Example: The following is a diagram of points A, B, C, and Q:
Intersection
The term intersect is used when lines, rays, line segments or figures meet, that is, they share a common point. The point they share is called the point of intersection. We say that these figures intersect.
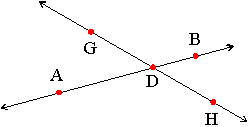
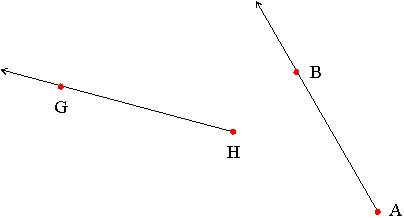
Example: In the diagram below, line AB and line GH intersect at point D:
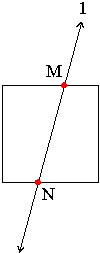
Example: In the diagram below, line 1 intersects the square in points M and N:
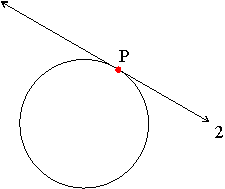
Example: In the diagram below, line 2 intersects the circle at point P:
Line Segments
A line segment is one of the basic terms in geometry. We may think of a line segment as a “straight” line that we might draw with a ruler on a piece of paper. A line segment does not extend forever, but has two distinct endpoints.
We write the name of a line segment with endpoints A and B as “line segment AB” or as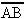 
. Note how there are no arrow heads on the line over AB such as when we denote a line or a ray.
Example: The following is a diagram of two line segments: line segment CD and line segment PN, or simply segment CD and segment PN.
Rays
A ray is one of the basic terms in geometry. We may think of a ray as a “straight” line that begins at a certain point and extends forever in one direction. The point where the ray begins is known as its endpoint. We write the name of a ray with endpoint A and passing through a point B as “ray AB” or as 
. Note how the arrow heads denotes the direction the ray extends in: there is no arrow head over the endpoint.
Example: The following is a diagram of two rays: ray HG and ray AB.
Endpoints
An endpoint is a point used to define a line segment or ray. A line segment has two endpoints; a ray has one.
Example: The endpoints of line segment DC below are points D and C, and the endpoint of ray MN is point M below:
Parallel Lines
Two lines in the same plane which never intersect are called parallel lines. We say that two line segments are parallel if the lines that they lie on are parallel. If line 1 is parallel to line 2, we write this as
line 1 || line 2
When two line segments DC and AB lie on parallel lines, we write this as
segment DC || segment AB.
Example: Lines 1 and 2 below are parallel
Example: The opposite sides of the rectangle below are parallel. The lines passing through them never meet.
Angles and Angle Terms
What is an Angle?
Two rays that share the same endpoint form an angle. The point where the rays intersect is called the vertex of the angle. The two rays are called the sides of the angle.
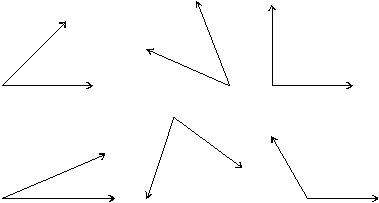
Example: Here are some examples of angles.
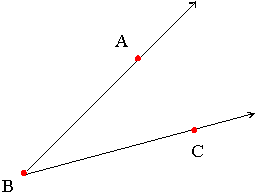
We can specify an angle by using a point on each ray and the vertex. The angle below may be specified as angle ABC or as angle CBA; you may also see this written as
ABC or as CBA. Note how the vertex point is always given in the middle.
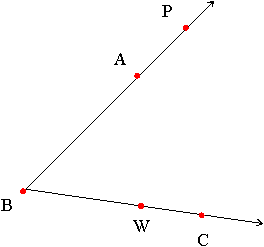
Example: Many different names exist for the same angle. For the angle below, PBC, PBW, CBP, and WBA are all names for the same angle.
Degrees: Measuring Angles
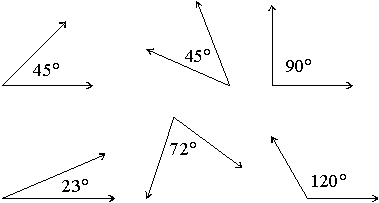
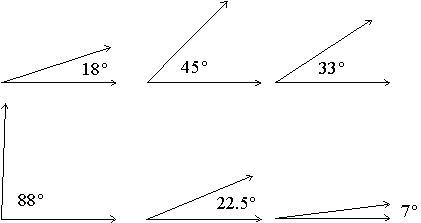
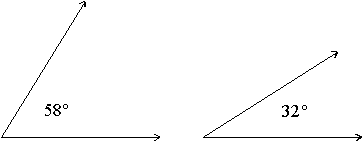
We measure the size of an angle using degrees.
Example: Here are some examples of angles and their degree measurements.
Acute Angles
An acute angle is an angle measuring between 0 and 90 degrees.
Example: The following angles are all acute angles.
Obtuse Angles
An obtuse angle is an angle measuring between 90 and 180 degrees.
Example: The following angles are all obtuse.
Right Angles
A right angle is an angle measuring 90 degrees. Two lines or line segments that meet at a right angle are said to be perpendicular. Note that any two right angles are supplementary angles (a right angle is its own angle supplement).
Example: The following angles are both right angles.
Complementary Angles
Two angles are called complementary angles if the sum of their degree measurements equals 90 degrees. One of the complementary angles is said to be the complement of the other.
Example: These two angles are complementary.
Note that these two angles can be “pasted” together to form a right angle!
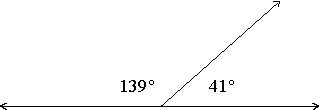
Supplementary Angles
Two angles are called supplementary angles if the sum of their degree measurements equals 180 degrees. One of the supplementary angles is said to be the supplement of the other.
Example: These two angles are supplementary.
Note that these two angles can be “pasted” together to form a straight line!
Vertical Angles
For any two lines that meet, such as in the diagram below, angle AEB and angle DEC are called vertical angles. Vertical angles have the same degree measurement. Angle BEC and angle AED are also vertical angles.
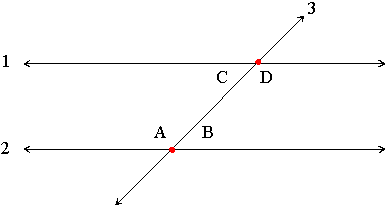
Alternate Interior Angles
For any pair of parallel lines 1 and 2, that are both intersected by a third line, such as line 3 in the diagram below, angle A and angle D are called alternate interior angles. Alternate interior angles have the same degree measurement. Angle B and angle C are also alternate interior angles.
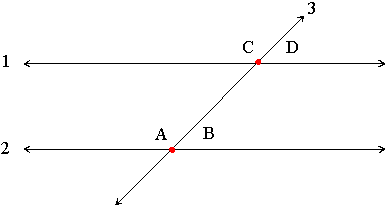
Alternate Exterior Angles
For any pair of parallel lines 1 and 2, that are both intersected by a third line, such as line 3 in the diagram below, angle A and angle D are called alternate exterior angles. Alternate exterior angles have the same degree measurement. Angle B and angle C are also alternate exterior angles.
Corresponding Angles
For any pair of parallel lines 1 and 2, that are both intersected by a third line, such as line 3 in the diagram below, angle A and angle C are called corresponding angles. Corresponding angles have the same degree measurement. Angle B and angle D are also corresponding angles.
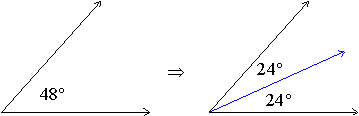
Angle Bisector
An angle bisector is a ray that divides an angle into two equal angles.
Example: The blue ray on the right is the angle bisector of the angle on the left.
The red ray on the right is the angle bisector of the angle on the left.
Perpendicular Lines
Two lines that meet at a right angle are perpendicular.
Figures and Polygons
Polygon
A polygon is a closed figure made by joining line segments, where each line segment intersects exactly two others.
Examples:
The following are examples of polygons:
The figure below is not a polygon, since it is not a closed figure:
The figure below is not a polygon, since it is not made of line segments:
The figure below is not a polygon, since its sides do not intersect in exactly two places each:
Regular Polygon
A regular polygon is a polygon whose sides are all the same length, and whose angles are all the same. The sum of the angles of a polygon with n sides, where n is 3 or more, is 180° × (n – 2) degrees.
Examples:
The following are examples of regular polygons:
Examples:
The following are not examples of regular polygons:
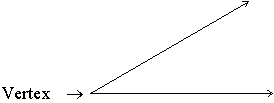
Vertex
1) The vertex of an angle is the point where the two rays that form the angle intersect.
2) The vertices of a polygon are the points where its sides intersect.
Triangle
A three-sided polygon. The sum of the angles of a triangle is 180 degrees.
Examples:
Equilateral Triangle or Equiangular Triangle
A triangle having all three sides of equal length. The angles of an equilateral triangle all measure 60 degrees.
Examples:
Isosceles Triangle
A triangle having two sides of equal length.
Examples:
Scalene Triangle
A triangle having three sides of different lengths.
Examples:
Acute Triangle
A triangle having three acute angles.
Examples:
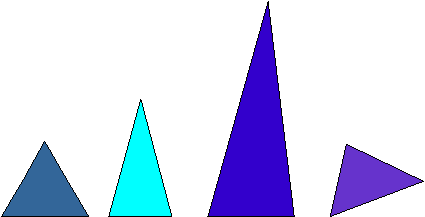
Obtuse Triangle
A triangle having an obtuse angle. One of the angles of the triangle measures more than 90 degrees.
Examples:
Right Triangle
A triangle having a right angle. One of the angles of the triangle measures 90 degrees. The side opposite the right angle is called the hypotenuse. The two sides that form the right angle are called the legs. A right triangle has the special property that the sum of the squares of the lengths of the legs equals the square of the length of the hypotenuse. This is known as the Pythagorean Theorem.
Examples:
Example:
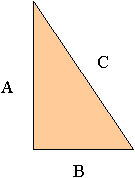
For the right triangle above, the lengths of the legs are A and B, and the hypotenuse has length C. Using the Pythagorean Theorem, we know that A2 + B2 = C2.
Example:
In the right triangle above, the hypotenuse has length 5, and we see that 32 + 42 = 52 according to the Pythagorean Theorem.
Quadrilateral
A four-sided polygon. The sum of the angles of a quadrilateral is 360 degrees.
Examples:
Rectangle
A four-sided polygon having all right angles. The sum of the angles of a rectangle is 360 degrees.
Examples:
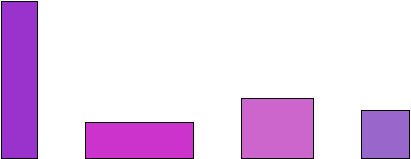
Square
A four-sided polygon having equal-length sides meeting at right angles. The sum of the angles of a square is 360 degrees.
Examples:
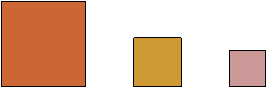
Parallelogram
A four-sided polygon with two pairs of parallel sides. The sum of the angles of a parallelogram is 360 degrees.
Examples:
Rhombus
A four-sided polygon having all four sides of equal length. The sum of the angles of a rhombus is 360 degrees.
Examples:
Trapezoid
A four-sided polygon having exactly one pair of parallel sides. The two sides that are parallel are called the bases of the trapezoid. The sum of the angles of a trapezoid is 360 degrees.
Examples:
Pentagon
A five-sided polygon. The sum of the angles of a pentagon is 540 degrees.
Example:
A regular pentagon:
An irregular pentagon:
Hexagon
A six-sided polygon. The sum of the angles of a hexagon is 720 degrees.
Examples:
A regular hexagon:
An irregular hexagon:
Heptagon
A seven-sided polygon. The sum of the angles of a heptagon is 900 degrees.
Examples:
A regular heptagon:
An irregular heptagon:
Octagon
An eight-sided polygon. The sum of the angles of an octagon is 1080 degrees.
Examples:
A regular octagon:
An irregular octagon:
Nonagon
A nine-sided polygon. The sum of the angles of a nonagon is 1260 degrees.
Examples:
A regular nonagon:
An irregular nonagon:
Decagon
A ten-sided polygon. The sum of the angles of a decagon is 1440 degrees.
Examples:
A regular decagon:
An irregular decagon:
Circle
A circle is the collection of points in a plane that are all the same distance from a fixed point. The fixed point is called the center. A line segment joining the center to any point on the circle is called a radius.
Example:
The blue line is the radius r, and the collection of red points is the circle.
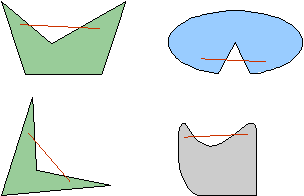
Convex
A figure is convex if every line segment drawn between any two points inside the figure lies entirely inside the figure. A figure that is not convex is called a concave figure.
Example:
The following figures are convex.
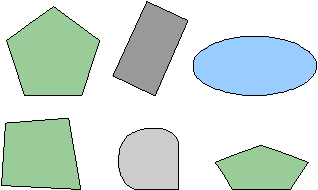
The following figures are concave. Note the red line segment drawn between two points inside the figure that also passes outside of the figure.
Area and Perimeter
Area
The area of a figure measures the size of the region enclosed by the figure. This is usually expressed in terms of some square unit. A few examples of the units used are square meters, square centimeters, square inches, or square kilometers.
Area of a Square
If l is the side-length of a square, the area of the square is l2 or l × l.
Example:
What is the area of a square having side-length 3.4?
The area is the square of the side-length, which is 3.4 × 3.4 = 11.56.
Area of a Rectangle
The area of a rectangle is the product of its width and length.
Example:
What is the area of a rectangle having a length of 6 and a width of 2.2?
The area is the product of these two side-lengths, which is 6 × 2.2 = 13.2.
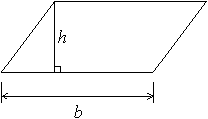
Area of a Parallelogram
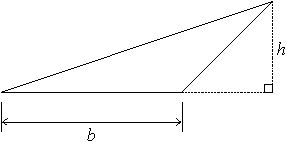
The area of a parallelogram is b × h, where b is the length of the base of the parallelogram, and h is the corresponding height. To picture this, consider the parallelogram below:
We can picture “cutting off” a triangle from one side and “pasting” it onto the other side to form a rectangle with side-lengths b and h. This rectangle has area b × h.
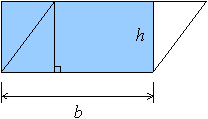
Example:
What is the area of a parallelogram having a base of 20 and a corresponding height of 7?
The area is the product of a base and its corresponding height, which is 20 × 7 = 140.
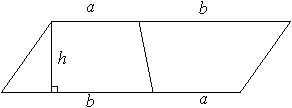
Area of a Trapezoid
If a and b are the lengths of the two parallel bases of a trapezoid, and h is its height, the area of the trapezoid is
1/2 × h × (a + b) .
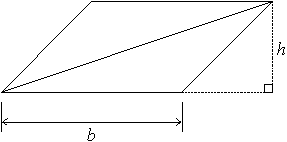
To picture this, consider two identical trapezoids, and “turn” one around and “paste” it to the other along one side as pictured below:
The figure formed is a parallelogram having an area of h × (a + b), which is twice the area of one of the trapezoids.
Example:
What is the area of a trapezoid having bases 12 and 8 and a height of 5?
Using the formula for the area of a trapezoid, we see that the area is
1/2 × 5 × (12 + 8) = 1/2 × 5 × 20 = 1/2 × 100 = 50.
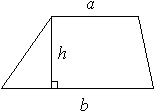
Area of a Triangle
or 
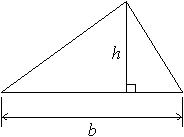
Consider a triangle with base length b and height h.
The area of the triangle is 1/2 × b × h.
To picture this, we could take a second triangle identical to the first, then rotate it and “paste” it to the first triangle as pictured below:
or 
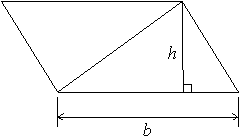
The figure formed is a parallelogram with base length b and height h, and has area b × ×h.
This area is twice that of the triangle, so the triangle has area 1/2 × b × h.
Example:
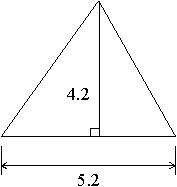
What is the area of the triangle below having a base of length 5.2 and a height of 4.2?
The area of a triangle is half the product of its base and height, which is 1/2 ×5.2 × 4.2 = 2.6 × 4.2 = 10.92..
Area of a Circle
The area of a circle is Pi × r2 or Pi × r × r, where r is the length of its radius. Pi is a number that is approximately 3.14159.
Example:
What is the area of a circle having a radius of 4.2 cm, to the nearest tenth of a square cm? Using an approximation of 3.14159 for Pi, and the fact that the area of a circle is Pi × r2, the area of this circle is Pi × 4.22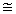 
3.14159 × 4.22 =55.41…square cm, which is 55.4 square cm when rounded to the nearest tenth.
Perimeter
The perimeter of a polygon is the sum of the lengths of all its sides.
Example:
What is the perimeter of a rectangle having side-lengths of 3.4 cm and 8.2 cm? Since a rectangle has 4 sides, and the opposite sides of a rectangle have the same length, a rectangle has 2 sides of length 3.4 cm, and 2 sides of length 8.2 cm. The sum of the lengths of all the sides of the rectangle is 3.4 + 3.4 + 8.2 + 8.2 = 23.2 cm.
Example:
What is the perimeter of a square having side-length 74 cm? Since a square has 4 sides of equal length, the perimeter of the square is 74 + 74 + 74 + 74 = 4 × 74 = 296.
Example:
What is the perimeter of a regular hexagon having side-length 2.5 m? A hexagon is a figure having 6 sides, and since this is a regular hexagon, each side has the same length, so the perimeter of the hexagon is 2.5 + 2.5 + 2.5 + 2.5 + 2.5 + 2.5 = 6 × 2.5 = 15m.
Example:
What is the perimeter of a trapezoid having side-lengths 10 cm, 7 cm, 6 cm, and 7 cm? The perimeter is the sum 10 + 7 + 6 + 7 = 30cm.
Circumference of a Circle
The distance around a circle. It is equal to Pi (π) times the diameter of the circle. Pi or π is a number that is approximately 3.14159.
Example:
What is the circumference of a circle having a diameter of 7.9 cm, to the nearest tenth of a cm? Using an approximation of 3.14159 for π, and the fact that the circumference of a circle is π times the diameter of the circle, the circumference of the circle is Pi × 7.9 π 3.14159 × 7.9 = 24.81…cm, which equals 24.8 cm when rounded to the nearest tenth of a cm.
Coordinates and Similar Figures
What is a Coordinate?
Coordinates are pairs of numbers that are used to determine points in a plane, relative to a special point called the origin. The origin has coordinates (0,0). We can think of the origin as the center of the plane or the starting point for finding all other points. Any other point in the plane has a pair of coordinates (x,y).
The x value or x-coordinate tells how far left or right the point is from the point (0,0), just like on the number line (negative is left of the origin, positive is right of the origin). The y value or y-coordinate tells how far up or down the point is from the point (0,0), (negative is down from the origin, positive is up from the origin). Using coordinates, we may give the location of any point we like by simply using a pair of numbers.
Example:
The origin below is where the x-axis and the y-axis meet. Point A has coordinates (2,3), since it is 2 units to the right and 3 units up from the origin. Point B has coordinates (3,0), since it is 3 units to the right, and lies on the x-axis. Point C has coordinates (6.3,9), since it is 6.3 units to the right, and 9 units up from the origin. Point D has coordinates (9,-2.5); it is 9 units to the right, and 2.5 units down from the origin. Point E has coordinates (-4,-3); it is 4 units to the left, and 3 units down from the origin. Point F has coordinates (-7,5.5); it is 7 units to the left, and 6 units up from the origin. Point G has coordinates (0,-7) since it lies on the y-axis 7 units below the origin.
Similar Figures
Figures that have the same shape are called similar figures. They may be different sizes or turned somewhat.
Example:
The following pairs of figures are similar.
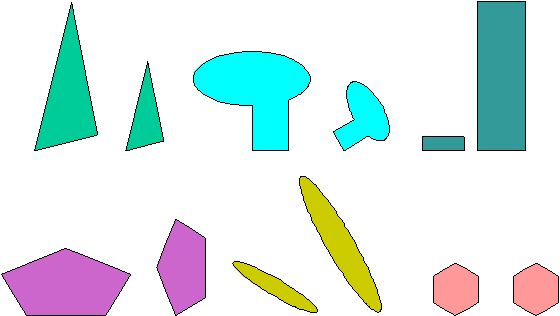
These pairs of figures are not similar.
Congruent Figures
Two figures are congruent if they have the same shape and size.
Example:
The following pairs of figures below are congruent. Note that if two figures are congruent, they must be similar.
The pairs below are similar but not congruent.
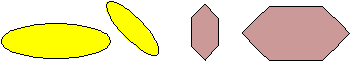
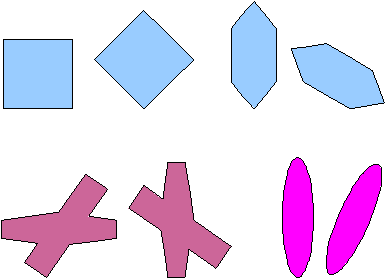
The pairs below are not similar or congruent.
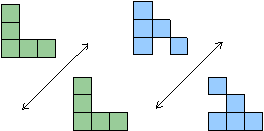
Rotation
When a figure is turned, we call it a rotation of the figure. We can measure this rotation in terms of degrees; a 360 degree turn rotates a figure around once back to its original position.
Example:
For the following pairs of figures, the figure on the right is a rotation of the figure on the left.
Reflection
If we flip (or mirror) along some line, we say the figure is a reflection along that line.
Examples:
Reflections along a vertical line:
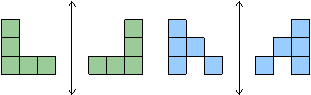
Reflections along a horizontal line:
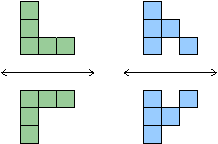
Reflections along a diagonal line:
Folding
When we talk about folding a plane figure, we mean folding it as if it were a piece of paper in that shape. We might fold this into a solid figure such as a box, or fold the figure flat along itself.
Example:
Folding the figure on the left into a box:
Folding the figure on the left flat along the dotted line:
Symmetric Figure
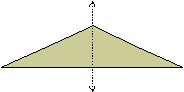
A figure that can be folded flat along a line so that the two halves match perfectly is a symmetric figure; such a line is called a line of symmetry.
Examples:
The triangle below is a symmetric figure. The dotted line is the line of symmetry.
The square below is a symmetric figure. It has four different lines of symmetry shown below.
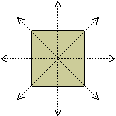
The rectangle below is a symmetric figure. It has two different lines of symmetry shown below.
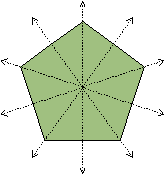
The regular pentagon below is a symmetric figure. It has five different lines of symmetry shown below.
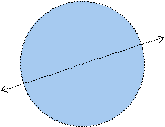
The circle below is a symmetric figure. Any line that passes through its center is a line of symmetry!
The figures shown below are not symmetric.
Space Figures and Basic Solids
Space Figure
A space figure or three-dimensional figure is a figure that has depth in addition to width and height. Everyday objects such as a tennis ball, a box, a bicycle, and a redwood tree are all examples of space figures. Some common simple space figures include cubes, spheres, cylinders, prisms, cones, and pyramids. A space figure having all flat faces is called a polyhedron. A cube and a pyramid are both polyhedrons; a sphere, cylinder, and cone are not.
Cross-Section
A cross-section of a space figure is the shape of a particular two-dimensional “slice” of a space figure.
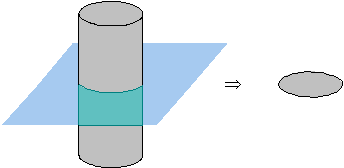
Example:
The circle on the right is a cross-section of the cylinder on the left.
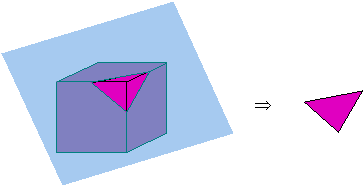
The triangle on the right is a cross-section of the cube on the left.
Volume
Volume is a measure of how much space a space figure takes up. Volume is used to measure a space figure just as area is used to measure a plane figure. The volume of a cube is the cube of the length of one of its sides. The volume of a box is the product of its length, width, and height.
Example:
What is the volume of a cube with side-length 6 cm?
The volume of a cube is the cube of its side-length, which is 63 = 216 cubic cm.
Example:
What is the volume of a box whose length is 4cm, width is 5 cm, and height is 6 cm?
The volume of a box is the product of its length, width, and height, which is 4 × 5 × 6 = 120 cubic cm.
Surface Area
The surface area of a space figure is the total area of all the faces of the figure.
Example:
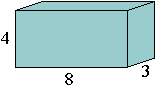
What is the surface area of a box whose length is 8, width is 3, and height is 4? This box has 6 faces: two rectangular faces are 8 by 4, two rectangular faces are 4 by 3, and two rectangular faces are 8 by 3. Adding the areas of all these faces, we get the surface area of the box:
8 × 4 + 8 × 4 + 4 × 3 + 4 × 3 + 8 × 3 + 8 × 3 =
32 + 32 + 12 + 12 +24 + 24=
136.
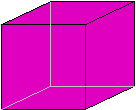
Cube
A cube is a three-dimensional figure having six matching square sides. If L is the length of one of its sides, the volume of the cube is L3 = L × L × L. A cube has six square-shaped sides. The surface area of a cube is six times the area of one of these sides.
Example:
The space figure pictured below is a cube. The grayed lines are edges hidden from view.
Example:
What is the volume and surface are of a cube having a side-length of 2.1 cm?
Its volume would be 2.1 × 2.1 × 2.1 = 9.261 cubic centimeters.
Its surface area would be 6 × 2.1 × 2.1 = 26.46 square centimeters.
Cylinder
A cylinder is a space figure having two congruent circular bases that are parallel. If L is the length of a cylinder, and r is the radius of one of the bases of a cylinder, then the volume of the cylinder is L × pi × r2, and the surface area is 2 × r × pi × L + 2 × pi × r2.
Example:
The figure pictured below is a cylinder. The grayed lines are edges hidden from view.
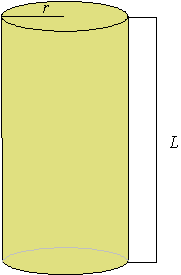
Sphere
A sphere is a space figure having all of its points the same distance from its center. The distance from the center to the surface of the sphere is called its radius. Any cross-section of a sphere is a circle.
If r is the radius of a sphere, the volume V of the sphere is given by the formula V = 4/3 × pi ×r3.
The surface area S of the sphere is given by the formula S = 4 × pi ×r2.
Example:
The space figure pictured below is a sphere.
Example:
To the nearest tenth, what is the volume and surface area of a sphere having a radius of 4cm?
Using an estimate of 3.14 for pi, the volume would be 4/3 × 3.14 × 43 = 4/3 × 3.14 × 4 × 4 × 4 = 268 cubic centimeters.
Using an estimate of 3.14 for pi, the surface area would be 4 × 3.14 × 42 = 4 × 3.14 × 4 × 4 = 201 square centimeters.
Cone
A cone is a space figure having a circular base and a single vertex.
If r is the radius of the circular base, and h is the height of the cone, then the volume of the cone is 1/3 × pi × r2 × h.
Example:
What is the volume in cubic cm of a cone whose base has a radius of 3 cm, and whose height is 6 cm, to the nearest tenth?
We will use an estimate of 3.14 for pi.
The volume is 1/3 × pi × 32 × 6 = pi ×18 = 56.52, which equals 56.5 cubic cm when rounded to the nearest tenth.
Example:
The pictures below are two different views of a cone.
Pyramid
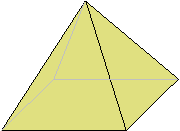
A pyramid is a space figure with a square base and 4 triangle-shaped sides.
Example:
The picture below is a pyramid. The grayed lines are edges hidden from view.
Tetrahedron
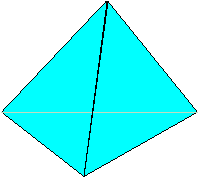
A tetrahedron is a 4-sided space figure. Each face of a tetrahedron is a triangle.
Example:
The picture below is a tetrahedron. The grayed lines are edges hidden from view.
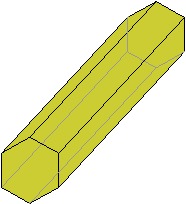
Prism
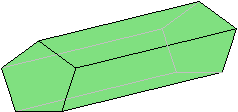
A prism is a space figure with two congruent, parallel bases that are polygons.
Examples:
The figure below is a pentagonal prism (the bases are pentagons). The grayed lines are edges hidden from view.
The figure below is a triangular prism (the bases are triangles). The grayed lines are edges hidden from view.
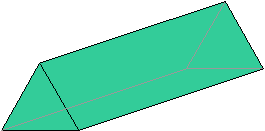
The figure below is a hexagonal prism (the bases are hexagons). The grayed lines are edges hidden from view..
