Math Sequences

Math sequences can be discovered in your everyday life. One’s earliest recollection of a math sequence probably began at the age of two, when you started counting to ten. A more relevant memory today might be one of you reciting your times table. Simply described, a math sequence is a group of numbers that follow a specific pattern. Each number within a mathematical sequence is identified as a term. Patterns within mathematical sequences provide the key that reveals a common thread of how each number is connected to one another.

Broadly speaking, mathematical sequences can be categorized into two major groups: arithmetic sequences (i.e. arithmetic progression) and geometrics sequences (i.e. geometric progression). You probably began differentiating between these two types of sequences while completing grade 11 math. Arithmetic sequences are defined by a string of consecutive numbers that have a common difference between them. A familiar example would encompass the sequence of house numbers along a street you happen to drive by (e.g. 102, 104, 106, 108 etc., common difference is 2.). Geometric sequences on the other hand encompass a succession of numbers that share a common ratio between them. For example, consider the half-life of a radioactive element – the common ratio is 2, and in a fixed amount of time, radioactive decay disintegrates the element by half.

Fibonacci Sequence

Not all mathematical sequences are easily separated into these two branches but are still incredibly interesting and applicable. One particular sequence that has garnered a strong reputation in it’s utility and ubiquity is the Fibonacci sequence. In the Fibonacci sequence, each number can be derived from the sum of the two preceding numbers. (i.e. 0, 1, 1, 2, 3, 5). Now where exactly have we observed this sequence of numbers over and over again in our everyday life? Not quite in numeric form as you might have guessed….

Fibonacci Spiral

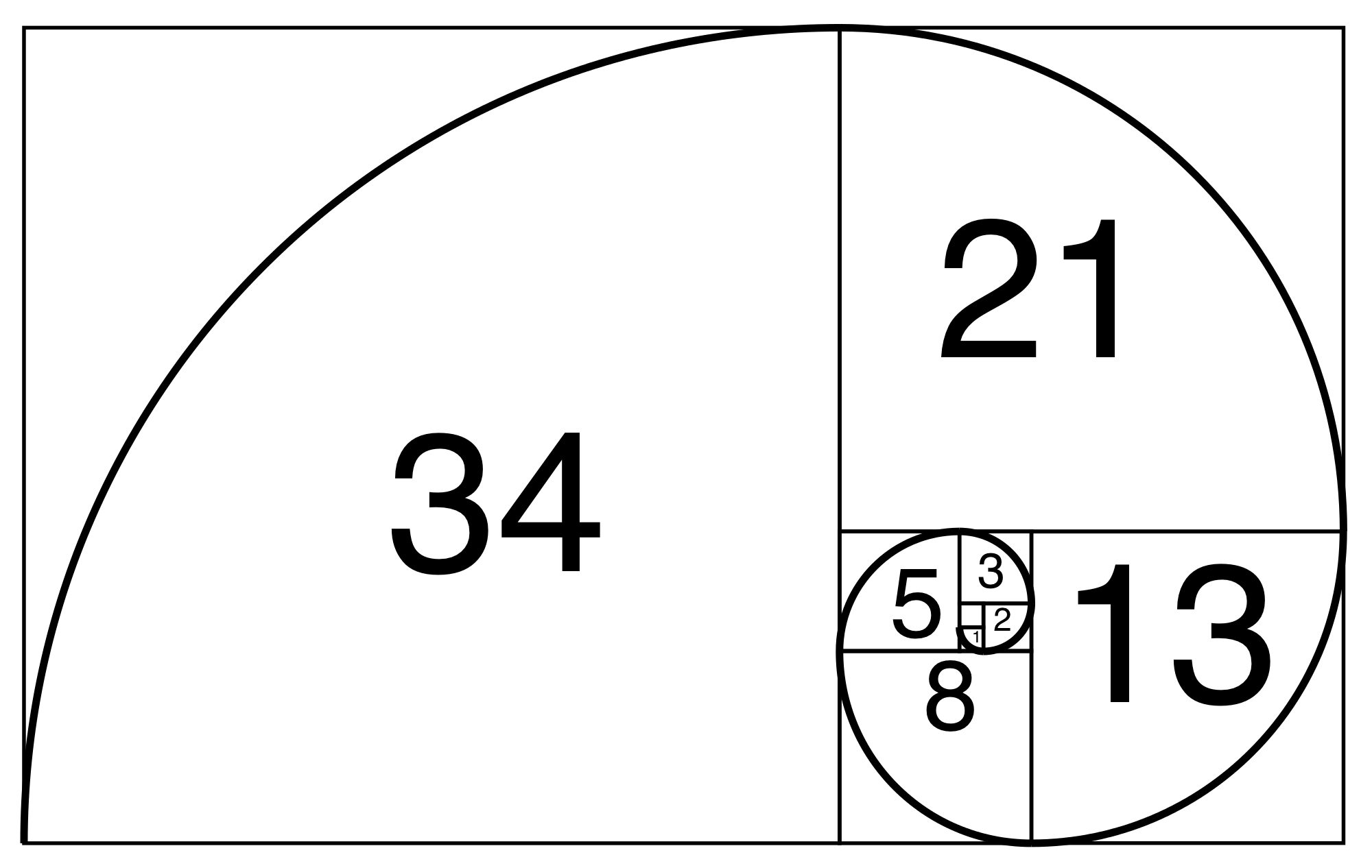
Also known as “the Golden Spiral”, in it’s most rudimentary form is outlined over a collection of squares that bear the dimensions of the Fibonacci sequence (1 x 1, 2 x 2, etc. see below). What appears to be an ordinary spiral forms unique quarter circles over each square that increases in size in according to the Fibonacci sequence.  All together these squares are fitted perfectly within what is known as a “golden rectangle”. The Fibonacci spiral however is not limited to rectangles (although this is the most common shape used to depict the Fibonacci spiral) and can be found in a multitude of geometric shapes (e.g. triangles) and real world entities, as we shall soon discover.

Golden Rectangle with the first few terms from the Fibonacci sequence. Each number indicates the dimensions of the square it is in Adapted from Dicklyon

The Golden Ratio

So what exactly is so grand and “Golden” about these shapes? Unsurprisingly, the astounding property of these shapes stems from their “Golden ratios” – 1:1.618. This value is originally derived from the ratio of two consecutive numbers in the Fibonacci sequence. Earlier on in the sequence, the ratio approaches 1.618, but is particularly more evident later in the sequence as the numbers grow larger and larger, the ratio between two consecutive numbers approaches a near perfect 1:1.618 ratio. So returning back to our example of the “golden rectangle”, what we would actually ascertain is that the ratio of its dimensions are 1:1.618.

Beauty in the eye of the Fibonacci Sequence

Many of the real world illustrations of the Fibonacci sequence portray what most would consider beauty. The most famous examples are found in nature. Several species of plants, in which the exact number of flower petals are always found to one that is found in the Fibonacci sequence. A more renowned example can be identified in the beloved sunflower. One will often discover that when counting the seed spirals of a sunflower in one direction (e.g. clock-wise), they will arrive at a number found in the Fibonacci sequence.  On the other hand, counting the number of seed spirals in the opposite direction (e.g. counter-clockwise) will result in tallying up to a successive or preceding number to the initial Fibonacci number counted in the clock-wise direction.

These Fibonacci spirals are found in a myriad of other atheistically pleasing entities such as galaxies, nautilus shells, hurricanes and as some would argue – in human faces.

The Fibonacci sequence/spirals and the rule of the golden ratio were said to also guide some of the most famous and celebrated pieces of classical (e.g. such as the Mona Lisa and the Last Supper) and modern arts

While the case of beauty may be rarely disputed for things of nature, the definition of beauty in humans is often in constant contention. In accordance to the Fibonacci sequence/spiral and the golden ratio, the most desirable human face has features of which proportions closely adhere to the golden ratio and spacing/distribution of features follows the squares found within golden rectangle. But how much can we trust this seemingly perfect sequence? How “golden” is this “golden ratio”? Does it really provide an equation of beauty or are we faced with a beast? Although the Fibonacci sequence existed long before the first fairy tales, their relevance has never been more prevalent in this day and age of vanity and the tireless pursuit of youth.

Let us consider some examples of “au-naturel” Fibonacci perfection in faces of celebrities:

1. Shinee Minho

2. Amber Heard

3. Kim Kardashian

Portrait of Kim Kardashian, Photo Credits: Glenn Francis, AKA Toglenn

Here popular vote and math converge in agreement that what we observe here is nothing short of beauty.

What about some other examples of faces that initially fail to meet the pre-requisites of “golden” perfection? Website designer, Igor K demonstrates how even after processing each portrait with multiple iterations/”corrections” of Fibonacci spirals and golden ratios, what results is still a mess: the kind that typically results when you’re playing around in Photobooth on your Mac OS…

1. Sylvester Stallone  

2. Nicholas Cage

3. Brian Cranston

Altogether these examples are a sure and striking beast of a difference compared to the eye candy previously observed.

Are we Golden?

So with a holistic perspective of the Fibonacci sequence/spiral and Golden ratio in practice, does this warp your view of the grandeur of these “golden rules”? While still an incredibly simple but complex, mathematical sequence, the Fibonacci sequence is still worthy of praise in the beauty that it does reveal to us in the real world. Our hope is that it also continues to receive recognition for its inability to paint a perfect picture every time. Such is a testament to the fact that extensive surgical makeovers don’t provide a quick fix for everyone and that perhaps the golden saying that ought to be taken to heart is that “Beauty is in the eye of the beholder”.

Interested in putting your face to the Fibonacci test? Check out these apps/simulation to see how well you fair!

• https://play.google.com/store/apps/details?id=com.facial.beauty.analysis&hl=en
• https://www.phimatrix.com/download/

For more help on other topics related to Math, visit StudyPug for a complete list of online tutoring services we provide.