Mastering Perpendicular Line Equations: A Comprehensive Guide Unlock the secrets of perpendicular line equations with our easy-to-follow guide. Learn formulas, solve problems, and boost your geometry skills. Perfect for students at all levels!
- Given the graph of linear equation, find the slope of perpendicular line equation.
- The lines 3y + 7x = 3 and cy - 2x - 1 = 0 are perpendicular. Find "c"
- Determine the equation of a line that is perpendicular to the line 3y + 5x = 8, and passes through the origin. Answer in slope intercept form and general form.
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Introduction
Welcome to our lesson on perpendicular line equations, a fundamental concept in geometry and algebra. We'll begin with an introduction video that provides a crucial foundation for understanding this topic. This video will help you visualize perpendicular lines and grasp their key properties. Throughout the lesson, we'll explore various methods for finding perpendicular line equations using different types of given information. You'll learn how to determine these equations from graphs, which offer a visual representation of the lines. We'll also cover techniques for finding perpendicular lines when given equations of other lines, allowing you to manipulate existing formulas. Additionally, we'll discuss how to derive perpendicular line equations using specific points. By mastering these skills, you'll be able to solve a wide range of problems involving perpendicular lines in both academic and real-world contexts. Let's dive in and unravel the mysteries of perpendicular line equations together!
Understanding how to visualize perpendicular lines is crucial for grasping their properties. When you can see how these lines interact, it becomes easier to apply the concepts to different scenarios. For instance, when you derive perpendicular line equations from given points, you can better understand the relationship between the lines. This skill is particularly useful in solving geometric problems and can be applied in various fields such as engineering and architecture. By practicing these techniques, you'll become proficient in identifying and working with perpendicular lines, enhancing your overall mathematical abilities.
Given the graph of linear equation, find the slope of perpendicular line equation.
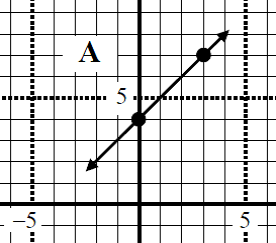
Step 1: Identify the Slope of the Given Line
To find the slope of the given line, you need to determine the rise over run. This means you need to see how much the line goes up (rise) and how much it goes over (run) between two points on the line. In the graph provided, you can see that the line goes up by 3 units and over by 3 units. Therefore, the slope (m) of the given line is calculated as follows:
Slope (m) = \frac{Rise}{Run} = \frac{3}{3} = 1
Step 2: Understand the Concept of Perpendicular Slopes
Perpendicular lines have slopes that are negative reciprocals of each other. This means if one line has a slope of m, the perpendicular line will have a slope of −m1. For example, if the slope of the original line is 1, the slope of the perpendicular line will be −11.
Step 3: Calculate the Perpendicular Slope
Given that the slope of the original line is 1, we need to find the negative reciprocal of this slope to determine the slope of the perpendicular line. The negative reciprocal of 1 is calculated as follows:
Perpendicular Slope=−11=−1
Step 4: Verify the Perpendicular Slope
To ensure that the calculated perpendicular slope is correct, you can verify by checking that the product of the slopes of the original line and the perpendicular line is -1. In this case:
Original Slope×Perpendicular Slope=1×(−1)=−1
Since the product is -1, the calculated perpendicular slope is indeed correct.
Conclusion
By following these steps, you can determine the slope of the perpendicular line to any given linear equation. In this example, the slope of the given line was found to be 1, and the slope of the perpendicular line was calculated to be -1. This method can be applied to any linear equation to find the slope of its perpendicular line.
Here are some frequently asked questions about perpendicular line equations:
1. What is the formula for finding a perpendicular line?
The formula for finding a perpendicular line is based on the fact that the slopes of perpendicular lines are negative reciprocals of each other. If the slope of the original line is m, the slope of the perpendicular line will be -1/m. The equation of the perpendicular line can be written as y - y1 = (-1/m)(x - x1), where (x1, y1) is a point on the perpendicular line.
2. How do you identify a perpendicular line?
You can identify a perpendicular line by checking if the product of the slopes of two lines is -1. If m1 and m2 are the slopes of two lines, they are perpendicular if m1 * m2 = -1. Additionally, perpendicular lines intersect at a 90-degree angle.
3. What is the formula for the perpendicular point on a line?
The formula for finding the perpendicular point from a point (x0, y0) to a line Ax + By + C = 0 is:
x = (B(Bx0 - Ay0) - AC) / (A² + B²)
y = (A(-Bx0 + Ay0) - BC) / (A² + B²)
4. How do you find the perpendicular slope of a line?
To find the perpendicular slope of a line, take the negative reciprocal of the original line's slope. If the original slope is m, the perpendicular slope is -1/m. For example, if a line has a slope of 2, its perpendicular line will have a slope of -1/2.
5. How do you write the equation of a line in perpendicular form?
To write the equation of a line in perpendicular form, use the point-slope form with the perpendicular slope and a point on the line. The general form is y - y1 = m_perpendicular(x - x1), where m_perpendicular is the negative reciprocal of the original slope, and (x1, y1) is a point on the perpendicular line.
To master the concept of perpendicular line equations, it's crucial to have a solid foundation in several prerequisite topics. Understanding these fundamental concepts will greatly enhance your ability to grasp and apply perpendicular line equations effectively.
One of the most important prerequisites is the point-slope form of a line. This form is essential because it provides a framework for understanding how lines are represented mathematically. By mastering this concept, you'll be better equipped to manipulate and analyze perpendicular lines.
Another key concept is the right angle intersection, which is fundamental to perpendicular lines. Understanding how lines intersect at right angles and the properties of these intersections is crucial for working with perpendicular line equations.
Familiarity with the coordinate plane is also vital. This knowledge provides the spatial context in which perpendicular lines are plotted and analyzed. It's the foundation for visualizing and interpreting perpendicular line equations graphically.
Graphing linear equations is another critical skill. This ability allows you to visualize perpendicular lines and understand their relationships in a two-dimensional space. It's an essential step in comprehending how perpendicular line equations work in practice.
Understanding vertical and horizontal lines is particularly important, as these are special cases of perpendicular lines. Recognizing how these lines behave and their unique properties will deepen your understanding of perpendicular line equations.
The skill of converting between forms of linear equations is also crucial. This ability allows you to move between different representations of lines, which is often necessary when working with perpendicular line equations.
Identifying slopes from equations is another key prerequisite. Since perpendicular lines have slopes that are negative reciprocals of each other, understanding how to identify and work with slopes is essential.
Finally, proficiency in solving linear equations is fundamental. This skill forms the basis for manipulating and solving perpendicular line equations, allowing you to find points of intersection and other important information.
By mastering these prerequisite topics, you'll build a strong foundation for understanding and working with perpendicular line equations. Each concept contributes to your overall comprehension, making the study of perpendicular lines more accessible and meaningful. Remember, mathematics is a cumulative subject, and each new concept builds upon previous knowledge. Take the time to reinforce these prerequisites, and you'll find that perpendicular line equations become much more manageable and intuitive.