Sign In
Try Free
 flag-uk

Horizontal and vertical distances

Topic Notes
In this section, we will be showing and describing transformations of given figures on coordinate planes. In the previous section, we used only one type of transformation for each question. In contrast, in this section, we will be using several types of transformations for each question. For example, we will be given a figure on a coordinate plane and asked to describe what combination of translations, reflections and rotations would need to occur to move this figure from one location to another on the plane.

Introduction to Transformations on Coordinate Planes

Transformations on coordinate planes are fundamental concepts in geometry that involve moving or altering geometric shapes. The three main types of transformations are translations on coordinate planes, reflections, and rotations. Translations involve sliding a figure in any direction without changing its size or shape. Reflections flip a figure over a line, creating a mirror image. Rotations turn a figure around a fixed point. Understanding these transformations is crucial for grasping more advanced geometric concepts. The introduction video provides a clear explanation of how to work with horizontal and vertical distances in transformations. This knowledge is essential for accurately plotting points and moving shapes on coordinate plane. By mastering these basic transformations, students can develop a strong foundation for more complex geometric operations and problem-solving skills. The video serves as an excellent starting point for exploring the fascinating world of coordinate geometry and spatial relationships.

Understanding Translations

Translations are a fundamental concept in geometry and coordinate mathematics. A translation is a type of transformation that moves every point of a figure or shape the same distance in the same direction on a coordinate plane. This movement doesn't change the size, shape, or orientation of the object; it simply shifts its position.

On a coordinate plane, translations affect points and shapes by changing their coordinates. For example, if we have a point at (3, 4) and translate it 2 units right and 1 unit up, its new position would be (5, 5). This concept applies to all points of a shape, moving points on coordinate plane uniformly.

To perform a translation, follow these steps:

  1. Identify the original coordinates of the point or shape.
  2. Determine the horizontal and vertical movements required.
  3. Add the horizontal movement to the x-coordinate of each point.
  4. Add the vertical movement to the y-coordinate of each point.

Let's look at some examples:

  • Horizontal movement: Moving a point (2, 3) five units to the right would result in (7, 3).
  • Vertical movement: Shifting a point (4, 1) three units up would give us (4, 4).
  • Combined movement: Translating a point (-1, 2) two units left and four units down would result in (-3, -2).

The notation for translations is typically expressed as (x, y) (x + a, y + b), where:

  • (x, y) represents the original coordinates
  • a is the horizontal movement (positive for right, negative for left)
  • b is the vertical movement (positive for up, negative for down)

Interpreting this notation is straightforward. For instance, (x, y) (x - 3, y + 5) means move 3 units left and 5 units up. This would transform a point (2, 1) to (-1, 6).

Visual examples are crucial for understanding translations. Imagine a triangle with vertices at (0, 0), (2, 0), and (1, 2). If we apply a translation of 3 units right and 1 unit down, represented as (x, y) (x + 3, y - 1), the new vertices would be:

  • (0, 0) (3, -1)
  • (2, 0) (5, -1)
  • (1, 2) (4, 1)

This translation would shift the entire triangle without changing its size or shape. On a coordinate grid, you would see the original triangle and its translated image, clearly showing the movement.

Translations have practical applications in various fields, including computer graphics, game development, and mapping. In these contexts, understanding how to move points on coordinate plane is essential for creating animations, designing user interfaces, or plotting geographic data.

It's important to note that translations are just one type of transformation in geometry. Others include rotations, reflections, and dilations. However, translations are unique in that they preserve all properties of the original shape, including size, angle measures, and orientation.

When working with translations, it's helpful to use graph paper or digital graphing tools to visualize the movements. This can make it easier to understand how the coordinates change and how the shape moves on the plane. Practice with various examples, including positive and negative movements in both directions, to gain a solid understanding of translations.

In conclusion, translations are a crucial concept in coordinate geometry, allowing us to move points and shapes on a plane while maintaining their essential properties. By understanding the notation, step-by-step process, and visual representations of translations, you can effectively apply this

Exploring Reflections on the Coordinate Plane

Reflections on a coordinate plane are fundamental transformations in geometry that play a crucial role in mathematics and various real-world applications. Unlike translations, which involve moving an object without changing its orientation, reflections create a mirror image of the original shape across a line of reflection. This concept is essential for understanding symmetry and spatial relationships in mathematics.

A reflection is a type of transformation that flips an object across a line, creating an exact mirror image. The line of reflection acts as an imaginary mirror, and every point of the original shape is reflected at an equal distance on the opposite side of this line. This process preserves the size and shape of the original figure but reverses its orientation.

There are several types of reflections commonly encountered on the coordinate plane:

  • Reflection over the x-axis: This reflection flips the shape vertically across the horizontal x-axis.
  • Reflection over the y-axis: This reflection flips the shape horizontally across the vertical y-axis.
  • Reflection over y = x: This diagonal reflection flips the shape across the line y = x.
  • Reflection over y = -x: This diagonal reflection flips the shape across the line y = -x.
  • Reflection over any other line: Reflections can occur over any line on the coordinate plane, not just the axes or diagonal lines.

To perform a reflection, follow these steps:

  1. Identify the line of reflection.
  2. For each point of the original shape, measure the perpendicular distance to the reflection line.
  3. Extend this perpendicular line an equal distance on the opposite side of the reflection line.
  4. Mark the new point at this location.
  5. Repeat for all points of the shape.
  6. Connect the new points to form the reflected shape.

For example, to reflect a triangle over the y-axis:

  1. Plot the original triangle on the coordinate plane.
  2. For each vertex, find its x-coordinate and change its sign while keeping the y-coordinate the same.
  3. Plot these new points and connect them to form the reflected triangle.

Determining the coordinates of reflected points depends on the line of reflection:

For reflections over other lines, more complex calculations may be required, often involving the distance formula and the equation of the reflection line.

Visual examples are particularly helpful in understanding reflections on a coordinate plane. Imagine a simple shape like a right triangle with vertices at (1, 1), (3, 1), and (1, 3). When reflected over the y-axis, its new vertices would be (-1, 1), (-3, 1), and (-1, 3). This creates a mirror image of the original triangle on the opposite side of the y-axis.

Reflections have numerous practical applications, from creating symmetrical designs in art and architecture to analyzing molecular structures in chemistry. In computer graphics, reflections are used to create realistic images and special effects. Understanding reflections on the coordinate plane provides a strong foundation for more advanced concepts in geometry and spatial reasoning.

As you explore reflections further, consider how they relate to other transformations like rotations and dilations. Practice identifying lines of symmetry in everyday objects and try to visualize how these objects would look when reflected across different lines. By mastering the concept of reflections, you'll enhance your spatial awareness and problem-solving skills in mathematics and beyond.

Mastering Rotations

Rotations are fundamental transformations in geometry that play a crucial role in various mathematical and real-world applications. A rotation is a movement of a point or shape around a fixed center point on a coordinate plane. This transformation preserves the size and shape of the original figure while changing its orientation. Understanding rotations is essential for students, engineers, and anyone working with spatial relationships.

The two key components of a rotation are the center of rotation and the angle of rotation. The center of rotation is the fixed point around which the object rotates. It can be any point on the coordinate plane, including the origin (0, 0) or a point on the object itself. The angle of rotation determines how far the object turns around the center. This angle is typically measured counterclockwise, although clockwise rotations are also possible by using negative angles.

To perform a rotation, follow these steps:

  1. Identify the center of rotation and the angle of rotation.
  2. For each point of the shape, measure the distance from the center of rotation.
  3. Rotate each point by the given angle around the center.
  4. Connect the rotated points to form the new shape.

Let's explore some common rotation angles and their effects:

  • 90° rotation: This quarter-turn rotation moves points counterclockwise by 90 degrees. For example, the point (x, y) rotated 90° around the origin becomes (-y, x).
  • 180° rotation: This half-turn rotation effectively flips the object upside down. The point (x, y) rotated 180° around the origin becomes (-x, -y).
  • 270° rotation: This three-quarter turn is equivalent to a -90° rotation. The point (x, y) rotated 270° around the origin becomes (y, -x).

Determining the coordinates of rotated points can be done using trigonometric functions or by applying specific formulas for common angles. For a general rotation of angle θ around the origin, the formulas are:

  • x' = x cos θ - y sin θ
  • y' = x sin θ + y cos θ

Where (x, y) are the original coordinates and (x', y') are the rotated coordinates.

When the center of rotation is not the origin, additional steps are required. First, translate the figure so that the center of rotation becomes the origin, then perform the rotation, and finally translate the figure back to its original position.

Visual examples are invaluable for understanding rotations. Imagine a square with vertices at (0, 0), (2, 0), (2, 2), and (0, 2). Rotating this square 90° counterclockwise around the origin would result in a new square with vertices at (0, 0), (0, 2), (-2, 2), and (-2, 0). This clearly shows how the shape maintains its size and proportions while changing its orientation on the coordinate plane.

Rotations have numerous practical applications, including:

  • Computer graphics and animation
  • Robotics and machine movement
  • Architectural design and engineering
  • Map making and navigation
  • Physics and astronomy

Understanding rotations also helps in grasping more complex mathematical concepts like vector transformations, matrix operations, and group theory. In the realm of symmetry, rotations play a crucial role in identifying and creating rotationally symmetric figures, which are prevalent in nature, art, and design.

To further enhance your understanding of rotations, practice with various shapes and angles. Start with simple figures like triangles and squares, then progress to more complex polygons. Experiment with different centers of rotation, including points inside and outside the shape. Use graph paper or digital tools to visualize the transformations and verify your calculations.

Combining Transformations

Understanding how to combine multiple transformations on a coordinate plane is a crucial skill in geometry. When working with transformations such as translations, reflections, and rotations, it's essential to follow a specific order of operations to achieve the desired result. This process allows us to manipulate points and shapes in complex ways, creating intricate geometric patterns and solving advanced problems.

The order of operations for multiple transformations is critical because different sequences can lead to different final positions. Generally, we perform transformations from left to right, just as we read. However, it's important to note that some transformations are commutative (can be done in any order), while others are not.

Let's explore how to combine different types of transformations:

1. Combined Translations

Translations are commutative, meaning they can be performed in any order. To combine multiple translations, simply add the horizontal and vertical components separately. For example, if we translate a point (x, y) by (2, 3) and then by (-1, 4), the final translation would be (2 + (-1), 3 + 4) = (1, 7).

2. Combined Reflections

Reflections are not commutative, so the order matters. When combining reflections, consider the following:

  • Two reflections over parallel lines result in a translation.
  • Two reflections over intersecting lines result in a rotation around the point of intersection.

To perform multiple reflections, apply them one at a time in the given order.

3. Combined Rotations

Rotations around the same center point are commutative. To combine rotations, simply add the angles. For example, a 45° rotation followed by a 90° rotation is equivalent to a single 135° rotation.

4. Mixing Different Transformations

When combining different types of transformations, follow these steps:

  1. Perform translations first
  2. Apply rotations second
  3. Execute reflections last

Here's a step-by-step guide to solving problems involving multiple transformations:

  1. Identify the given transformations and their order.
  2. Start with the original coordinates of the point or shape.
  3. Apply each transformation in order, calculating new coordinates after each step.
  4. Keep track of intermediate results to avoid errors.
  5. Double-check your final answer by verifying it satisfies all the given transformations.

Visual examples can greatly aid in understanding complex transformations. Consider the following scenario:

Example: Transform point A(2, 3) using these steps:

  1. Translate 4 units right and 2 units up
  2. Rotate 90° clockwise around the origin
  3. Reflect over the y-axis

Solution:

  1. After translation: A'(6, 5)
  2. After rotation: A''(5, -6)
  3. After reflection: A'''(-5, -6)

Visualizing this process on a coordinate plane helps to understand how each transformation affects the point's position. It's beneficial to sketch each step or use graphing software to illustrate the transformations clearly.

In conclusion, mastering the combination of multiple transformations requires practice and a solid understanding of each individual transformation. By following the correct order of operations and methodically applying each transformation, you can solve complex geometric problems and create intricate designs. Remember to use visual aids whenever possible to enhance your understanding and verify your results. With these skills, you'll be well-equipped to tackle advanced geometry problems involving multiple transformations.

Practical Applications and Problem-Solving

Transformations on coordinate planes are not just abstract mathematical concepts; they have numerous real-world applications across various fields. In this section, we'll explore how these transformations are used in computer graphics, engineering, and architecture, and provide practice problems to reinforce your understanding.

Real-World Applications

1. Computer Graphics: In the world of digital animation and video game design, transformations are essential. Developers use translations to move objects across the screen, rotations to spin characters or scenery, and scaling to resize elements. For instance, when a character in a video game jumps, it's essentially a vertical translation applied to the character's coordinates.

2. Engineering: Engineers use transformations when designing mechanical parts or analyzing structures. For example, in robotics, the movement of a robotic arm can be described using a series of rotations and translations. Civil engineers might use transformations to model how a building responds to different forces, such as wind or earthquakes.

3. Architecture: Architects frequently employ transformations in their designs. They might use reflections to create symmetrical building facades, or scaling to adjust the size of design elements. When creating 3D models of buildings, architects use a combination of translations, rotations, and scaling to position and orient different components.

Practice Problems

Let's now tackle some practice problems involving horizontal and vertical distances in transformations.

Problem 1:

A point A(3, 4) is translated 5 units right and 2 units down. What are the coordinates of the new point A'?

Solution:

  1. Horizontal translation: 5 units right means adding 5 to the x-coordinate
  2. Vertical translation: 2 units down means subtracting 2 from the y-coordinate
  3. New x-coordinate: 3 + 5 = 8
  4. New y-coordinate: 4 - 2 = 2
  5. Therefore, A'(8, 2)

Problem 2:

A rectangle reflection y-axis has vertices at (0, 0), (4, 0), (4, 3), and (0, 3). If it's reflected over the y-axis, what are the coordinates of the new vertices?

Solution:

  1. Reflection over the y-axis changes the sign of the x-coordinates
  2. (0, 0) remains (0, 0)
  3. (4, 0) becomes (-4, 0)
  4. (4, 3) becomes (-4, 3)
  5. (0, 3) remains (0, 3)

Problem 3:

A triangle with vertices at (1, 1), (3, 1), and (2, 3) is rotated 90° clockwise around the origin. What are the new coordinates?

Solution:

  1. For a 90° clockwise rotation: (x, y) becomes (y, -x)
  2. (1, 1) becomes (1, -1)
  3. (3, 1) becomes (1, -3)
  4. (2, 3) becomes (3, -2)

Problem 4:

A square with side length 2 units has its center at (1, 1). If it's scaled by a factor of 3, what are the coordinates of its vertices?

Solution:

  1. Original vertices: (0, 0), (2, 0), (2, 2), (0, 2)
  2. Scaling from the center

Conclusion

In this article, we've explored the fundamental concepts of transformations on coordinate planes. We covered translations, which involve moving points horizontally and vertically; reflections, which create mirror images across lines; and rotations, which involve turning points around a central axis. Understanding horizontal and vertical distances is crucial in performing these transformations accurately. To solidify your grasp of these concepts, we encourage you to rewatch the introductory video, which provides a comprehensive overview of the topic. Remember, mastering transformations requires practice and hands-on experience. Take time to work through additional problems, experiment with different types of transformations, and visualize how shapes change on the coordinate plane. By engaging actively with this material, you'll develop a strong foundation in geometric transformations, which is essential for more advanced mathematical concepts. Don't hesitate to seek additional resources or ask questions to deepen your understanding of transformations on coordinate planes.

Example:

Use translations, reflections and rotations to get the swimmer to the boat.
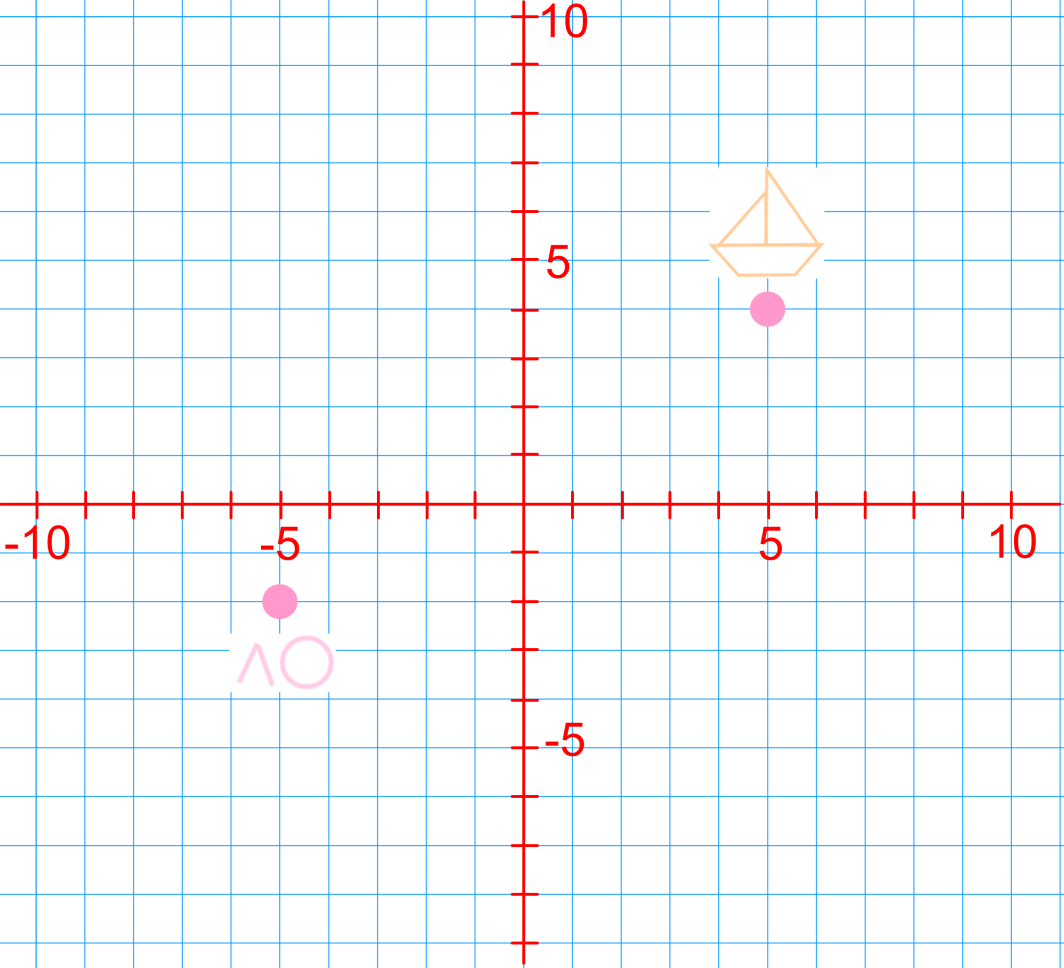
Moving the swimmer to the destination using translations, reflections and rotations

Step 1: Reflection

The first step to move the swimmer to the boat is to use a reflection. We will reflect the swimmer across the y-axis. Imagine the y-axis as our line of reflection, which we will label as R. To perform the reflection, we need to draw a line that is perpendicular to the y-axis from the swimmer's current position. This line will help us determine the new position of the swimmer after the reflection.

Start by counting the number of units the swimmer is from the y-axis. Suppose the swimmer is 5 units to the left of the y-axis. To reflect the swimmer, we will move the same number of units to the right of the y-axis. Therefore, the swimmer will be 5 units to the right of the y-axis after the reflection.

Step 2: Translation

After reflecting the swimmer, the next step is to use a translation to move the swimmer vertically. We need to move the swimmer up along the y-axis to align with the boat's position. Since both the swimmer's new position and the boat are at the same x-coordinate (x = 5), we do not need to move left or right.

To determine how many units to move up, count the number of units from the swimmer's current position to the boat's position. Suppose the swimmer needs to move up 6 units to reach the boat. We will translate the swimmer 6 units up along the y-axis.

Step 3: Final Position

After performing the reflection and translation, the swimmer will have reached the boat. The reflection moved the swimmer to the right side of the y-axis, and the translation moved the swimmer vertically up to the boat's position. By following these steps, we have successfully used translations, reflections, and rotations to get the swimmer to the boat.

FAQs

Here are some frequently asked questions about transformations on coordinate planes:

  1. What are the three main types of transformations on coordinate planes?

    The three main types of transformations on coordinate planes are translations, reflections, and rotations. Translations involve moving a shape in any direction without changing its size or orientation. Reflections create a mirror image of a shape across a line. Rotations involve turning a shape around a fixed point.

  2. How do you perform a translation on a coordinate plane?

    To perform a translation, add the horizontal movement to the x-coordinate and the vertical movement to the y-coordinate of each point. For example, to translate a point (3, 4) by 2 units right and 1 unit up, the new coordinates would be (5, 5).

  3. What happens when you reflect a shape over the y-axis?

    When reflecting a shape over the y-axis, the x-coordinates of all points change sign while the y-coordinates remain the same. For instance, a point at (3, 2) would be reflected to (-3, 2).

  4. How do you rotate a point 90 degrees clockwise around the origin?

    To rotate a point 90 degrees clockwise around the origin, swap the x and y coordinates and change the sign of the new y-coordinate. For example, the point (2, 3) rotated 90 degrees clockwise becomes (3, -2).

  5. Why is the order important when combining different transformations?

    The order of transformations is important because different sequences can lead to different final positions. Generally, translations are performed first, followed by rotations, and then reflections. Changing this order can result in a different final position for the transformed shape.

Prerequisite Topics

Understanding horizontal and vertical distances is crucial in mathematics, particularly in geometry and algebra. To fully grasp this concept, it's essential to have a solid foundation in several prerequisite topics. These topics provide the necessary skills and knowledge to comprehend and apply the principles of horizontal and vertical distances effectively.

One fundamental prerequisite is Conics - Circle, which involves moving shapes on the coordinate plane. This topic helps students visualize how objects can be positioned and moved in two-dimensional space, directly relating to the concept of horizontal and vertical distances.

Another important prerequisite is understanding reflection across the x-axis. This concept teaches students how to manipulate shapes and points by flipping them over the x-axis, which is crucial when dealing with vertical distances. Similarly, reflection across the y-axis is equally important, as it relates to horizontal distances and how objects can be mirrored on the coordinate plane.

The study of parallel and perpendicular line equations is particularly relevant when exploring horizontal and vertical distances. This topic helps students understand the relationships between lines and how to calculate the perpendicular distance to a reflection line, which is often a key component in problems involving horizontal and vertical distances.

Lastly, combining transformations of functions is a critical prerequisite. This topic teaches students how to apply multiple transformations to a function or shape, which is often necessary when working with complex problems involving horizontal and vertical distances.

By mastering these prerequisite topics, students will be well-equipped to tackle more advanced concepts related to horizontal and vertical distances. They will have the necessary tools to visualize and manipulate shapes on a coordinate plane, understand reflections and their impact on distances, work with parallel and perpendicular lines, and apply multiple transformations to solve complex problems.

It's important to note that these prerequisites build upon each other, creating a strong foundation for understanding horizontal and vertical distances. For example, the knowledge gained from studying conics and circles can be applied when working with reflections, which in turn helps in understanding parallel and perpendicular lines. This interconnectedness of topics highlights the importance of thoroughly grasping each prerequisite before moving on to more advanced concepts.

In conclusion, a solid understanding of these prerequisite topics is essential for students to fully comprehend and apply the principles of horizontal and vertical distances. By investing time in mastering these foundational concepts, students will be better prepared to tackle more complex problems and applications in geometry and algebra.

Basic Concepts
Related Concepts