Factorial notation
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practice With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practice on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
Get the most by viewing this topic in your current grade. Pick your course now.
Examples
Lessons
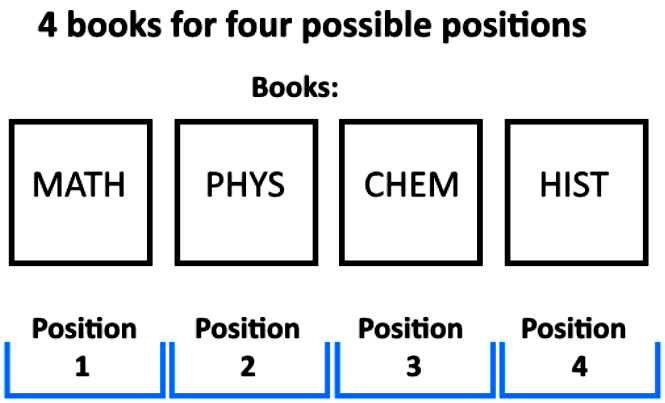
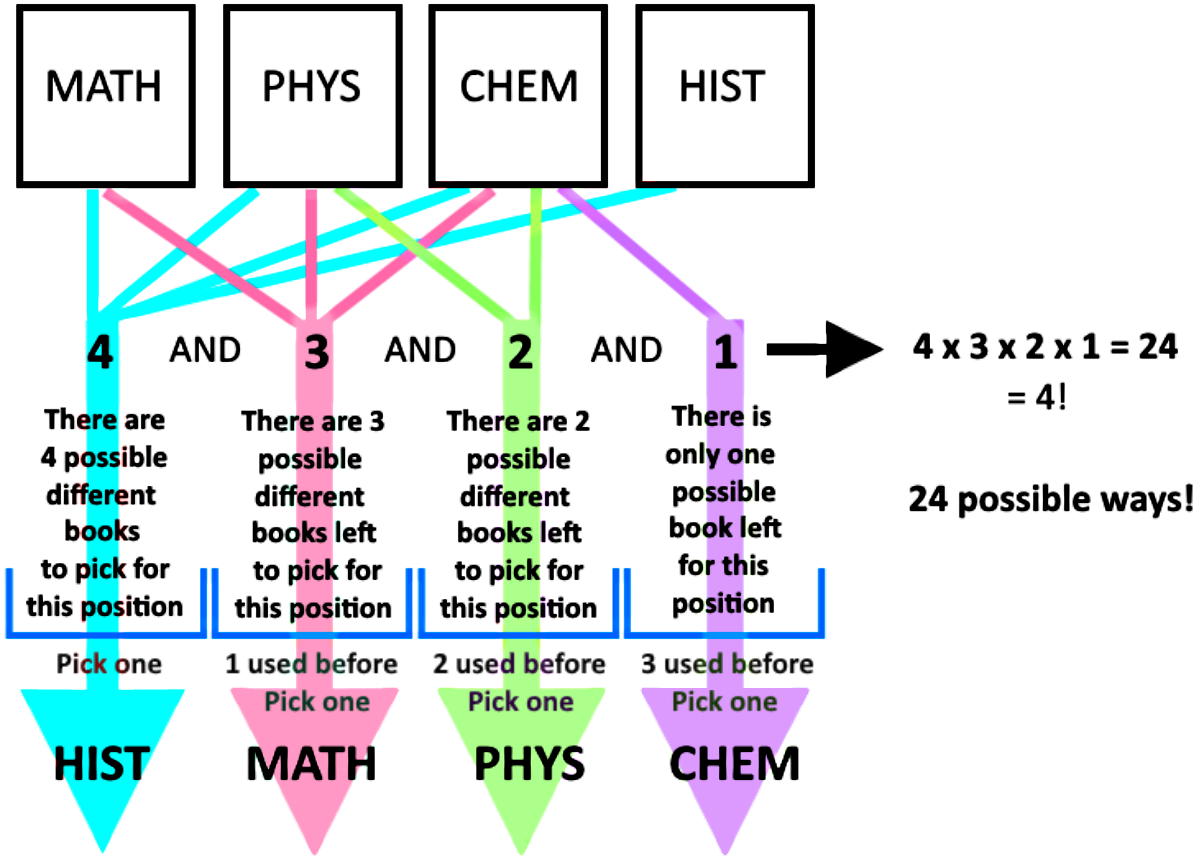
- How many ways are there to arrange 4 different books side by side on a bookshelf?
- factorial notation: n! = n (n-1) (n-2) (n-3) (n-4) . . . . . (5) (4) (3) (2) (1)
by definition : 0! = 1 - arrangement of words "without repititions" = n!
Determine the number of different arrangements of all the letters in the following words:- DOG
- MATH
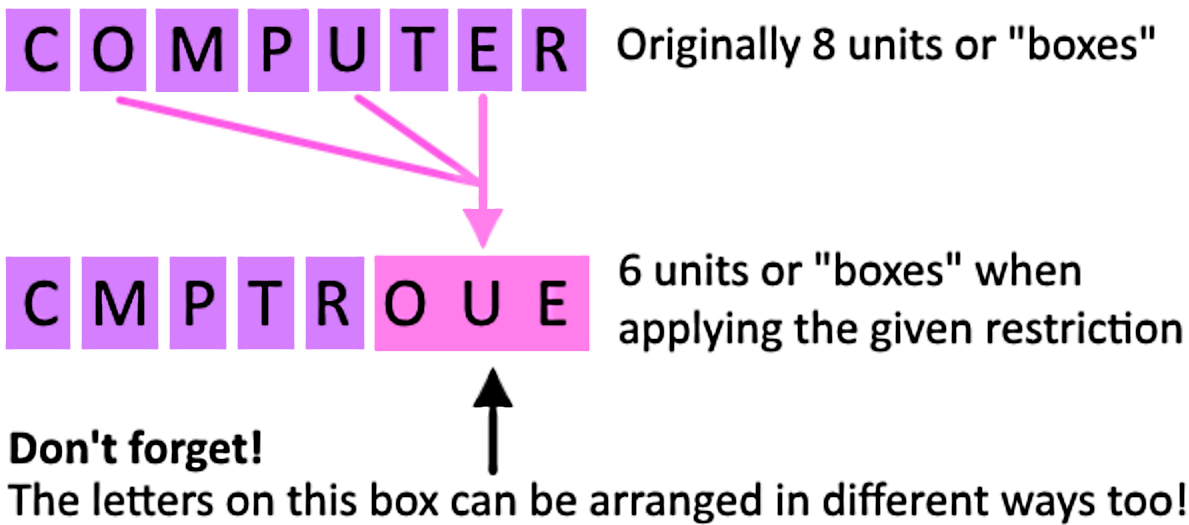
- COMPUTER
- arrangement of words "with repititions" =
Determine the number of different arrangements of all the letters in the following words: - arrangement with restrictions: must deal with the restrictions first!
- Determine the number of different arrangements of all the letters in the word: COMPUTER
(i) if there are no restrictions
(ii) if the vowels must be together
(iii) the vowels must not be together - i) How many ways are there to arrange 3 Math books (Math 10, Math 11, Math 12), 2 physics books (Phys 11, Phys 12), and 5 English (Eng 8, Eng 9, Eng 10, Eng 11, Eng 12) on a bookshelf?
ii) What if the books on each subject must be kept together?
- seating arrangement
- How many ways can 4 girls and 4 boys sit in a row, if:
i) they can sit anywhere?
ii) all the girls must sit together, and all the boys must sit together?
iii) all the girls must sit together, while the boys can pick their own seats?
iv) girls and boys alternate? - There are 3 couples, and they need to sit together. How many different ways can these 3 couples sit in a row?
- There are 7 people A, B, C, D, E, F, and G sitting in a row. How many different seating arrangements are there, if:
i) A must be to the left of B, but they do not need to sit together?
ii) A and B must sit together?
iii) A and B cannot sit together?
- How many ways can 4 girls and 4 boys sit in a row, if:
- Seating arrangements are considered to be different only when the positions of the people are different relative to each other.
How many seating arrangements are possible for 7 people sitting around a round table?