|
|
|
|
- Introduction to Horizontal Asymptotes
- Introduction to Horizontal Asymptotesopposite relationship between "vertical asymptote" and "horizontal asymptote"
- Introduction to Horizontal Asymptoteshow horizontal asymptotes are defined on each end of a function
- evaluate limits at infinity algebraically –"Highest Power Rule"!
- lesson overview
- Relate Asymptotes to Limits
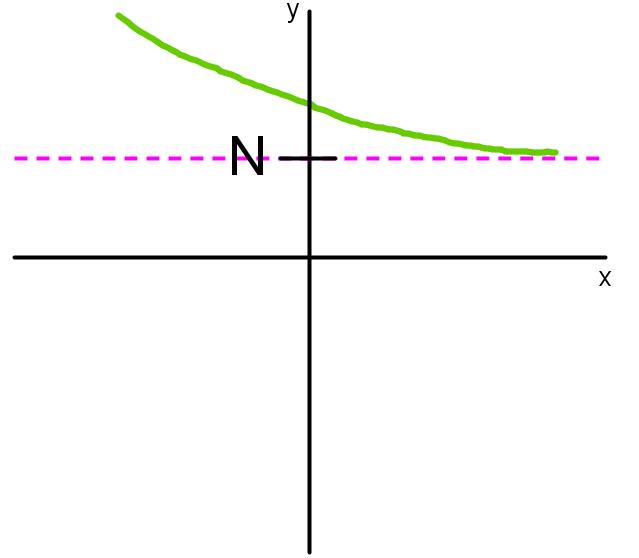
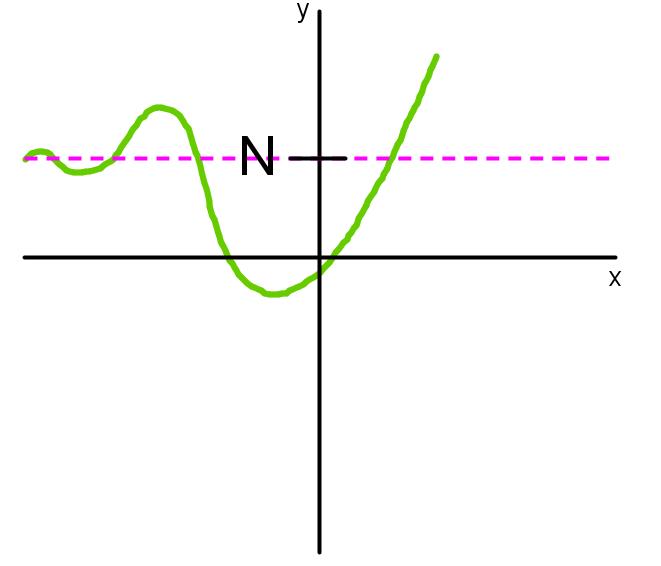
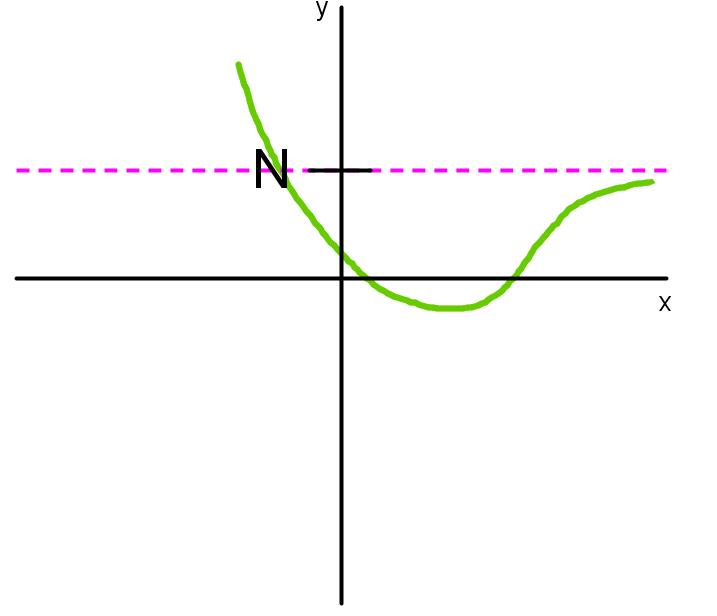
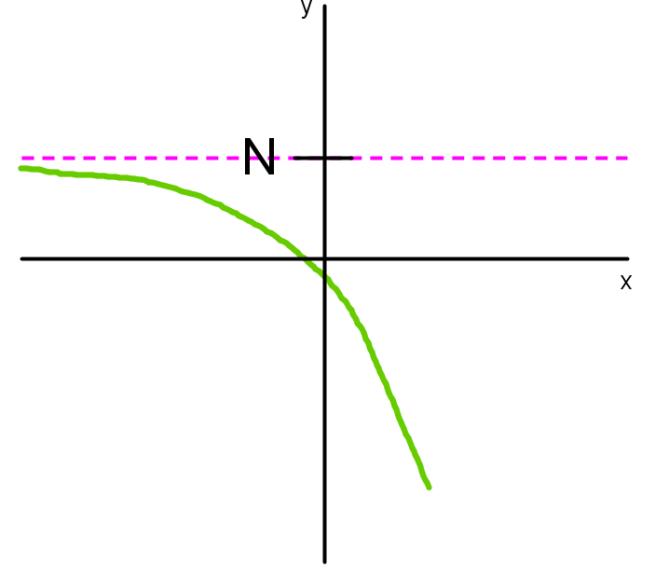
Express all asymptotes in limit notations for the function f whose graph is shown below.
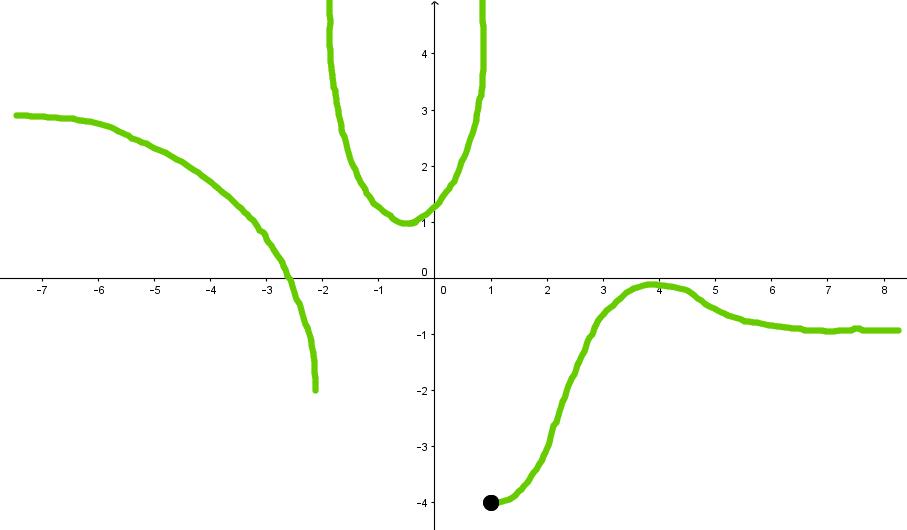
- Discuss the Foundation of Limits at Infinity
Find:
i) limx→∞x1
ii) limx→−∞x1 - Use "Highest Power Rule" to Evaluate Limits at Infinity of Rational Functions in 3 Types
Find: - Evaluate Limits at Infinity of Functions Involving Radicals
Find the horizontal asymptotes of the function f(x)=5x+83x2+7x−1000 by evaluating:
i) limx→∞5x+83x2+7x−1000
ii) limx→−∞5x+83x2+7x−1000 - Multiply Conjugates First, then Evaluate Limits
Find: - Infinite Limits at Infinity
Find:
i) limx→∞x3
ii) limx→−∞x3 - Ambiguous Case: ∞−∞
Find limx→∞x2−x - Limits at Infinity of Exponential Functions
Find:
i) limx→∞ex
ii) limx→−∞ex - Limits at Infinity of Trigonometric Functions
Find limx→∞sinx
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Introduction to Limits at Infinity and Horizontal Asymptotes
Welcome to our exploration of limits at infinity and horizontal asymptotes! These concepts are crucial in calculus, helping us understand how functions behave as x approaches infinity. Our introduction video is a great starting point, offering a visual and intuitive approach to these sometimes challenging ideas. Limits at infinity describe the long-term behavior of a function as x grows infinitely large or small. Horizontal asymptotes, on the other hand, are horizontal lines that a function's graph approaches but never quite reaches. They're closely related to limits at infinity and often represent the "end behavior" of a function. Understanding these concepts will give you powerful tools for analyzing graphs and predicting function behavior. As we dive deeper, you'll see how these ideas apply to real-world scenarios and form the foundation for more advanced calculus topics. Let's start this exciting journey together!
Introduction to Horizontal Asymptotes opposite relationship between "vertical asymptote" and "horizontal asymptote"
Step 1: Understanding Vertical Asymptotes
In the previous lesson, we discussed vertical asymptotes. A vertical asymptote occurs when the limit of a function approaches infinity as the input approaches a certain value. This is represented in limit notation as the limit of a function f(x) as x approaches a value c, resulting in either positive or negative infinity. For example, if the limit of f(x) as x approaches 2 is positive infinity, this indicates a vertical asymptote at x = 2. This means that as x gets closer to 2 from either direction, the function's value increases without bound.
Step 2: Graphical Representation of Vertical Asymptotes
To visualize this, consider the graph of a function with a vertical asymptote at x = 2. As x approaches 2 from the left, the function's value increases towards positive infinity. Similarly, as x approaches 2 from the right, the function's value also increases towards positive infinity. This behavior indicates that the function has a vertical asymptote at x = 2. Beyond the vicinity of x = 2, the function can behave in various ways, but near x = 2, it will always approach infinity.
Step 3: Introduction to Horizontal Asymptotes
Now, let's explore the opposite concept: horizontal asymptotes. Horizontal asymptotes occur when the limit of a function approaches a finite value as the input approaches infinity. This is the opposite of vertical asymptotes, where the function's value approaches infinity as the input approaches a finite value. In limit notation, for horizontal asymptotes, we switch the positions of infinity and the finite value. For example, if the limit of f(x) as x approaches infinity is 2, this indicates a horizontal asymptote at y = 2.
Step 4: Graphical Representation of Horizontal Asymptotes
To visualize this, consider the graph of a function with a horizontal asymptote at y = 2. As x approaches a very large positive value (such as 1 million or 1 billion), the function's value gets closer and closer to 2. This means that as we move further to the right on the graph, the function's value approaches 2. The function can exhibit various behaviors for smaller values of x, but as x becomes very large, the function will approach the value 2, indicating a horizontal asymptote at y = 2.
Step 5: Opposite Relationship Between Vertical and Horizontal Asymptotes
The relationship between vertical and horizontal asymptotes is opposite in both a literal and mathematical sense. Vertically, a function approaches infinity as the input approaches a finite value, while horizontally, a function approaches a finite value as the input approaches infinity. This opposite relationship is reflected in the limit notation, where the positions of infinity and the finite value are switched. Understanding this relationship helps in analyzing the behavior of functions and their asymptotes.
Step 6: Practical Application
To apply this knowledge, consider a function where you need to determine the asymptotes. First, identify any vertical asymptotes by finding the values of x that cause the function to approach infinity. Then, identify any horizontal asymptotes by examining the behavior of the function as x approaches infinity. This dual approach allows for a comprehensive understanding of the function's behavior and its asymptotic properties.
Here are some frequently asked questions about limits at infinity and horizontal asymptotes:
-
What is a limit at infinity?
A limit at infinity describes the behavior of a function as the input (x) approaches positive or negative infinity. It helps us understand how the function's output changes as x becomes extremely large or small.
-
How do you find horizontal asymptotes?
To find horizontal asymptotes, compare the degrees of the numerator and denominator in a rational function. If the numerator's degree is less than the denominator's, the asymptote is y=0. If they're equal, divide the leading coefficients. If the numerator's degree is greater, there's no horizontal asymptote.
-
What's the difference between a vertical and horizontal asymptote?
Vertical asymptotes occur at specific x-values where the function approaches infinity. Horizontal asymptotes describe the function's behavior as x approaches infinity, showing a y-value the function gets close to but never reaches.
-
Can a function cross its horizontal asymptote?
Yes, a function can cross its horizontal asymptote. The asymptote describes the function's long-term behavior, but the function may oscillate around or cross this line at finite x-values.
-
How are limits at infinity used in real-world applications?
Limits at infinity are used in various fields. In physics, they help analyze terminal velocity. In economics, they're used to predict long-term market trends. In engineering, they assist in understanding system behavior over extended periods.
To fully grasp the concept of limits at infinity and horizontal asymptotes, it's crucial to have a solid foundation in several prerequisite topics. Understanding these fundamental concepts will significantly enhance your ability to analyze and interpret the behavior of functions as they approach infinity.
One of the key prerequisites is vertical asymptotes. While horizontal asymptotes deal with the behavior of functions as x approaches infinity, vertical asymptotes focus on points where the function grows without bound. This contrast helps in understanding the different types of asymptotic behavior.
The highest power rule is essential when evaluating limits at infinity. This rule helps determine the dominant term in a function as x grows large, which is crucial for identifying horizontal asymptotes.
Simplifying complex fractions is another vital skill. When dealing with rational functions and their limits at infinity, the ability to simplify and analyze these fractions is indispensable for determining the existence and value of horizontal asymptotes.
Proficiency in factoring trinomials is also important. This skill allows you to break down complex polynomial expressions, which is often necessary when analyzing the behavior of functions as they approach infinity.
Exponential function graph analysis provides insights into how certain functions behave as x approaches positive or negative infinity. This knowledge is directly applicable to understanding horizontal asymptotes in exponential contexts.
Similarly, trigonometric function graph analysis is beneficial. While trigonometric functions don't typically have horizontal asymptotes, understanding their graphical behavior enhances overall function analysis skills.
Interestingly, even concepts from economics, such as market equilibrium, can provide a practical context for understanding asymptotic behavior. In economics, equilibrium points often represent a kind of "asymptote" in market behavior, offering a real-world analogy to mathematical limits.
By mastering these prerequisite topics, you'll be well-equipped to tackle the complexities of limits at infinity and horizontal asymptotes. Each concept builds upon the others, creating a comprehensive understanding of function behavior and asymptotic analysis. This foundational knowledge not only aids in solving specific problems but also develops a deeper, more intuitive grasp of calculus concepts, setting you up for success in more advanced mathematical studies.



