Adding and subtracting mixed numbers
Topic Notes
Introduction
Welcome to our lesson on subtracting mixed fractions, a crucial skill in mathematics. To begin, we'll explore an introduction video that provides a visual foundation for understanding this concept. This video is essential as it demonstrates the process step-by-step, making it easier to grasp the fundamentals. Throughout this lesson, we'll delve into the intricacies of subtracting mixed fractions, which involves working with numbers that combine whole numbers and fractions. We'll cover various scenarios, including cases where you need to convert mixed numbers to improper fractions before performing the subtraction. This conversion is sometimes necessary to simplify the process and avoid errors. By mastering these techniques, you'll be able to confidently approach problems involving mixed fractions in both academic and real-world contexts. Remember, practice is key to becoming proficient in subtracting mixed fractions, so be sure to work through the examples and exercises provided.
Understanding Mixed Fractions and Improper Fractions
Mixed fractions and improper fractions are two different ways of representing numbers that are not whole. Understanding the difference between these two forms and how to convert between them is crucial, especially when performing operations like subtraction. Let's explore these concepts in detail.
Mixed Fractions
A mixed fraction consists of a whole number and a proper fraction. For example, 3 1/4 is a mixed fraction where 3 is the whole number part and 1/4 is the proper fraction part. Mixed fractions are often used in everyday life as they are easier to visualize and understand.
Improper Fractions
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. For instance, 13/4 is an improper fraction. Improper fractions represent values that are greater than or equal to 1.
Converting Between Mixed Fractions and Improper Fractions
Converting between these two forms is an essential skill, particularly when performing mathematical operations. Here's how to do it:
Mixed Fraction to Improper Fraction:
- Multiply the whole number by the denominator.
- Add this result to the numerator.
- Place this sum over the original denominator.
Example: Convert 3 1/4 to an improper fraction
(3 × 4) + 1 = 13
13/4
Improper Fraction to Mixed Fraction:
- Divide the numerator by the denominator.
- The quotient becomes the whole number part.
- The remainder becomes the numerator of the fractional part.
- The denominator remains the same.
Example: Convert 13/4 to a mixed fraction
13 ÷ 4 = 3 remainder 1
3 1/4
Importance in Subtracting Mixed Fractions
When subtracting mixed fractions, it's often necessary to convert them to improper fractions first. This is because subtracting mixed fractions can be tricky, especially when borrowing is required. By converting to improper fractions, the subtraction process becomes more straightforward.
Example:
Subtract 2 3/4 from 5 1/2
Step 1: Convert to improper fractions
5 1/2 = 11/2
2 3/4 = 11/4
Step 2: Find a common denominator (in this case, 4)
11/2 = 22/4
Step 3: Subtract
22/4 - 11/4 = 11/4
Step 4: Convert back to a mixed fraction
11/4 = 2 3/4
Visual Representations
Visual aids can greatly enhance understanding of these concepts. Imagine a pie chart divided into four parts. Three whole pies and one quarter of another pie visually represent 3 1/4. The same amount can be shown as 13 quarters of a pie, representing 13/4.
Conclusion
Mastering the conversion between mixed fractions and improper fractions is a fundamental skill in mathematics. It not only aids in performing operations like subtraction but also helps in developing a deeper understanding of fractional numbers. Practice these conversions regularly to become proficient in working with fractions in various forms.
Finding Common Denominators
Finding common denominators is a crucial step in subtracting fractions, as it allows us to perform operations on fractions with different denominators. This process ensures that we're comparing and manipulating fractions with the same base, making calculations more accurate and straightforward. Common denominators are essential because they create equivalent fractions that represent the same value but with a shared denominator, enabling us to add or subtract the numerators directly.
One of the primary methods for finding common denominators is using the least common multiple (LCM) of the original denominators. The LCM is the smallest positive number that is divisible by both denominators. Using the LCM as the common denominator ensures we're working with the simplest possible equivalent fractions. To find the LCM, we can use various techniques such as listing multiples, prime factorization, or the upside-down division method.
Let's walk through a step-by-step example of finding common denominators for the fractions 1/4 and 3/5:
- Identify the denominators: 4 and 5
- Find the LCM of 4 and 5:
- List multiples of 4: 4, 8, 12, 16, 20
- List multiples of 5: 5, 10, 15, 20
- The LCM is 20
- Convert each fraction to an equivalent fraction with the denominator 20:
- 1/4 = (1 × 5)/(4 × 5) = 5/20
- 3/5 = (3 × 4)/(5 × 4) = 12/20
Now we have equivalent fractions with a common denominator: 5/20 and 12/20. These can be easily subtracted by simply subtracting the numerators: 12/20 - 5/20 = 7/20.
Another method for finding common denominators is to multiply the denominators together. While this always works, it may result in larger numbers than necessary. For example, with 1/4 and 3/5, we could use 4 × 5 = 20 as the common denominator, which in this case happens to be the LCM as well.
For more complex fractions, such as 2/6 and 5/9, we can follow a similar process:
- Identify the denominators: 6 and 9
- Find the LCM of 6 and 9:
- Prime factorization: 6 = 2 × 3, 9 = 3 × 3
- LCM = 2 × 3 × 3 = 18
- Convert each fraction to an equivalent fraction with the denominator 18:
- 2/6 = (2 × 3)/(6 × 3) = 6/18
- 5/9 = (5 × 2)/(9 × 2) = 10/18
Now we have 6/18 and 10/18, which can be easily subtracted: 10/18 - 6/18 = 4/18.
Understanding and applying the concept of common denominators is fundamental in fraction arithmetic. It allows us to perform operations on fractions with different denominators by creating equivalent fractions that share the same denominator. This skill is not only crucial for basic fraction operations but also forms the foundation for more advanced mathematical concepts involving rational numbers and algebraic fractions.
Subtracting Mixed Fractions with Like Denominators
Subtracting mixed fractions with like denominators is a fundamental skill in mathematics that builds upon basic fraction operations. This process involves working with whole numbers and proper fractions simultaneously, and sometimes requires the technique of borrowing. Let's explore this concept in detail, providing clear examples and a step-by-step guide to master this important mathematical operation.
When subtracting mixed fractions with like denominators, the first step is to align the whole numbers and fractions separately. The like denominators make the process simpler, as we don't need to find a common denominator. Here's a straightforward example:
5 3/8 - 2 1/8 = 3 2/8 = 3 1/4
In this case, we subtract the whole numbers and fractions (5 - 2 = 3) and the fractions (3/8 - 1/8 = 2/8) separately. The result is then simplified if possible.
However, subtraction becomes more complex when the fractional part of the minuend (the number we're subtracting from) is smaller than the fractional part of the subtrahend (the number we're subtracting). In such cases, we need to borrow from the whole number. This process is similar to borrowing in whole number subtraction but requires an additional step of converting the whole number to a fraction.
Let's look at an example where borrowing is necessary:
4 1/5 - 2 3/5
Here, we can't directly subtract 3/5 from 1/5. We need to borrow from the whole number. The step-by-step process for borrowing is as follows:
- Borrow 1 from the whole number part of the minuend. This reduces the whole number by 1 (4 becomes 3).
- Convert the borrowed 1 to a fraction with the same denominator as the existing fractions. In this case, 1 = 5/5 (because the denominator is 5).
- Add this fraction to the existing fraction in the minuend. 1/5 + 5/5 = 6/5.
- Now perform the subtraction with the new mixed fraction: 3 6/5 - 2 3/5
- Subtract the whole numbers: 3 - 2 = 1
- Subtract the fractions: 6/5 - 3/5 = 3/5
- Combine the results: 1 3/5
So, 4 1/5 - 2 3/5 = 1 3/5
It's important to note that after borrowing, we're essentially working with an improper fraction in the minuend (3 6/5). This allows us to perform the subtraction without encountering negative fractions.
Here's another example to reinforce the concept:
7 2/9 - 3 5/9
Following the borrowing process:
- Borrow 1 from 7, leaving 6 as the whole number.
- Convert 1 to 9/9 (because the denominator is 9).
- Add 9/9 to 2/9: 2/9 + 9/9 = 11/9
- Now we have: 6 11/9 - 3 5/9
- Subtract whole numbers: 6 - 3 = 3
- Subtract fractions: 11/9 - 5/9 = 6/9
- Combine: 3 6/9, which simplifies to 3 2/3
In this case, we also need to perform subtracting fractions with borrowing to get the correct result.
By practicing these steps and understanding the process of subtracting fractions with borrowing, you can master the skill of subtracting mixed fractions with like denominators.
Subtracting Mixed Fractions with Unlike Denominators
Subtracting mixed fractions with unlike denominators is a multi-step process that requires careful attention to detail. This operation is common in advanced arithmetic and algebra, and mastering it is crucial for solving complex mathematical problems. Let's break down the process step-by-step and explore both simple and complex cases.
The first step in subtracting mixed fractions with unlike denominators is to find a common denominator. This is essential because fractions can only be subtracted when they have the same denominator. To find a common denominator, we need to determine the least common multiple (LCM) of the original denominators. For example, if we're subtracting 2 3/4 from 5 1/2, we need to find the LCM of 4 and 2, which is 4.
Once we have the common denominator, we need to convert the fractions to equivalent fractions with this new denominator. In our example, 5 1/2 would become 5 2/4. The whole number remains the same, but we multiply both the numerator and denominator of the fractional part by 2 to get an equivalent fraction with the common denominator.
After conversion, we can proceed with the subtraction. However, before we subtract, we need to convert the mixed fractions to improper fractions. This is done by multiplying the whole number by the denominator and adding the numerator, then placing this sum over the denominator. For 5 2/4, we get (5 * 4 + 2) / 4 = 22/4. For 2 3/4, we get (2 * 4 + 3) / 4 = 11/4.
Now we can perform the subtraction: 22/4 - 11/4 = 11/4. To convert this back to a mixed fraction, we divide 11 by 4, getting 2 with a remainder of 3. So our final answer is 2 3/4.
In more complex cases, borrowing may be necessary. Let's consider subtracting 3 7/8 from 5 1/3. First, we find the common denominator: the LCM of 8 and 3 is 24. We convert the fractions: 5 1/3 becomes 5 8/24, and 3 7/8 becomes 3 21/24. Now, we can't directly subtract 21/24 from 8/24 because 8 is smaller than 21. This is where borrowing comes in.
To borrow, we take one whole from 5, converting it to 24/24. Now we have 4 32/24 (because 8/24 + 24/24 = 32/24). We can now subtract: 4 32/24 - 3 21/24 = 1 11/24. This is our final answer, as it's already in its simplest form.
It's important to note that in some cases, after subtraction, we may need to simplify the resulting fraction. For instance, if we end up with a fraction like 14/24, we would simplify this to 7/12 by dividing both the numerator and denominator by their greatest common factor (2 in this case).
Mastering the subtraction of mixed fractions with unlike denominators requires practice and attention to detail. The key steps to remember are: find a common denominator, convert fractions, change to improper fractions, subtract, and then convert back to a mixed fraction if necessary. Always be prepared for the possibility of borrowing, especially in more complex problems.
By following these steps and practicing with various examples, you'll become proficient in handling these types of mathematical operations. Remember, the process may seem complex at first, but with regular practice, it becomes more intuitive and manageable. Whether you're working on academic assignments, preparing for standardized tests, or applying these skills in real-world scenarios, understanding how to subtract mixed fractions with unlike denominators is a valuable mathematical skill to possess.
Converting to Improper Fractions Method
When subtracting mixed fractions, an alternative approach involves converting them to improper fractions first. This method can be particularly efficient in certain scenarios and offers a streamlined process for those comfortable with improper fraction arithmetic. Let's explore this technique step-by-step and compare its effectiveness to other methods.
Step 1: Convert mixed fractions to improper fractions
To convert a mixed fraction (a b/c) to an improper fraction:
- Multiply the whole number (a) by the denominator (c)
- Add this result to the numerator (b)
- Place this sum over the original denominator
Formula: (a × c + b) / c
Step 2: Perform the subtraction
Once both mixed fractions are converted to improper fractions, subtract as you would with any fractions, ensuring common denominators if necessary.
Step 3: Simplify the result
Reduce the resulting fraction if possible and convert back to a mixed fraction if desired.
Example: Let's subtract 3 1/4 - 1 2/3 1. Convert to improper fractions: 3 1/4 = (3 × 4 + 1) / 4 = 13/4 1 2/3 = (1 × 3 + 2) / 3 = 5/3 2. Find a common denominator (12): 13/4 = 39/12 5/3 = 20/12 3. Subtract: 39/12 - 20/12 = 19/12 4. Simplify (if needed): 19/12 = 1 7/12
Efficiency comparison: The improper fraction method can be more efficient when: - Dealing with complex mixed fractions - Working with fractions that have large whole numbers - Performing multiple operations in sequence It eliminates the need to borrow from the whole number part, which can be error-prone in more complex calculations. However, for simpler mixed fractions, the traditional method of subtracting whole numbers and fractions separately might be quicker and more intuitive for some.
When to prefer this method: 1. In algebraic manipulations where keeping fractions improper simplifies further steps 2. When working with fraction calculators or computer algorithms that prefer improper fractions 3. In problems involving multiple operations where maintaining improper form throughout can reduce steps 4. When teaching students a unified approach to fraction arithmetic, as this method works consistently for addition, subtraction, multiplication, and division
While this method may require an extra step of conversion at the beginning and end, it often simplifies the core arithmetic process, especially for more complex fractions. By eliminating the need to work with mixed numbers during the calculation, it reduces the chance of errors in borrowing or carrying over values. Additionally, for those who frequently work with fractions, becoming proficient in this method can lead to faster and more accurate calculations across various mathematical contexts.
Common Mistakes and How to Avoid Them
Subtracting mixed fractions can be challenging for many students, and several common errors often arise during this process. One of the most frequent mistakes is forgetting to borrow when the fractional part of the first number is smaller than that of the second. This oversight can lead to incorrect results and confusion. Another common error occurs when students incorrectly convert mixed numbers to improper fractions, which can throw off the entire calculation.
To avoid these pitfalls, it's crucial to follow a step-by-step approach and double-check each stage of the problem. When dealing with mixed fractions where borrowing is necessary, students should remember to convert the whole number to an improper fraction and combine it with the existing fraction before subtracting. This method ensures that the subtraction can be performed accurately without negative fractions.
Estimation is a powerful tool for error prevention. Before diving into the detailed calculation, students should roughly estimate the answer. This quick mental math can serve as a reality check, helping to identify glaring mistakes in the final result. For instance, if subtracting 2 3/4 from 5 1/2, a student should recognize that the answer will be slightly less than 3.
Another effective strategy is to consistently check answers. After completing the subtraction, students should add their result back to the number they subtracted and see if it equals the original number. This reverse-checking method can catch many errors that might otherwise go unnoticed. Additionally, converting all mixed numbers to improper fractions before subtracting can simplify the process and reduce the likelihood of borrowing mistakes.
Practice is key to mastering mixed fraction subtraction. Students should work through various problem types, gradually increasing in difficulty. This approach helps build confidence and familiarity with different scenarios, making it easier to spot potential errors. Teachers and parents can support this learning process by providing diverse practice mixed fraction problems and encouraging the use of visual aids, such as fraction bars or number lines, to reinforce conceptual understanding.
Lastly, it's important for students to understand the concept of equivalent fractions. Many errors occur when students try to subtract fractions with different denominators without first finding a common denominator for mixed fractions. By emphasizing the importance of like denominators and practicing the process of finding them, students can avoid this common pitfall and approach mixed fraction subtraction with greater accuracy and confidence.
Conclusion
In this lesson on subtracting mixed fractions, we've covered essential key points to master this important mathematical concept. The introduction video provided a crucial foundation for understanding the process. Remember to always convert mixed fractions to improper fractions, find a common denominator, and then subtract. Practice with the provided examples to reinforce your skills and build confidence. If you're struggling, don't hesitate to seek additional help from your teacher or online resources. Subtracting mixed fractions is a fundamental skill that will serve you well in more advanced mathematical topics. We encourage you to explore related concepts such as adding mixed fractions and working with complex fractions. Keep practicing and challenging yourself to improve your mathematical abilities. For further learning, check out our additional resources on fraction operations and algebra. Your journey in mathematics is just beginning, and mastering these skills will open doors to more advanced topics.
Example:
Subtract or add using the given diagram.
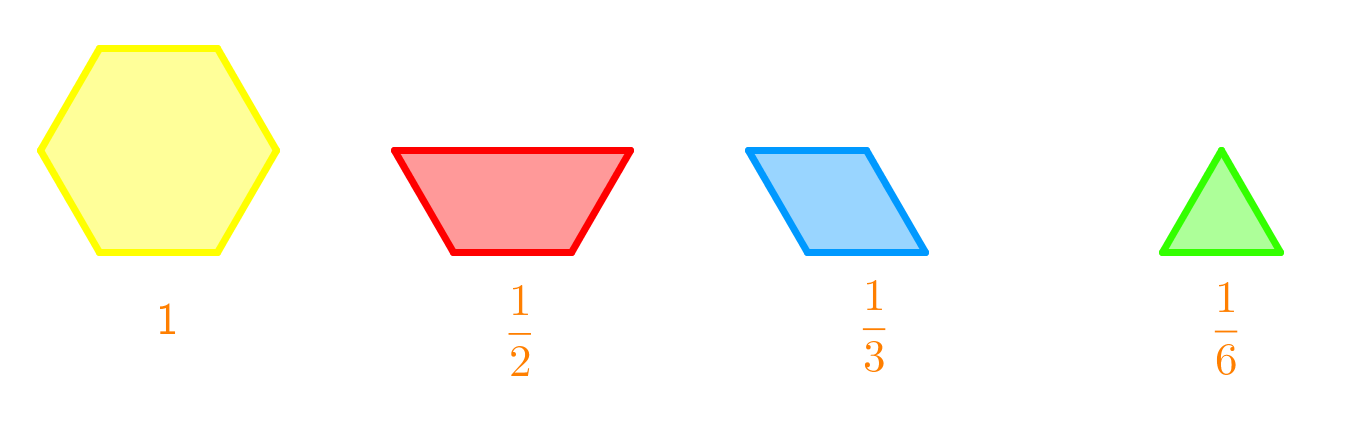

Step 1: Identify the Shapes and Their Values
First, examine the given diagram. Notice the different shapes and their corresponding values. The yellow shape represents the whole number 1. The blue shapes each represent one-third (1/3), and there are two of them. The green triangles each represent one-sixth (1/6), and there are three of them.
Step 2: Convert Shapes to Fractions
Next, convert the shapes into fractions. The yellow shape is 1. The two blue shapes are each 1/3, so together they make 1/3 + 1/3 = 2/3. The three green triangles are each 1/6, so together they make 1/6 + 1/6 + 1/6 = 3/6.
Step 3: Combine the Fractions
Now, combine the fractions. Start with the whole number 1. Add the two blue shapes (2/3) to it. This gives you 1 + 2/3. Then, add the three green triangles (3/6) to this sum. So, you have 1 + 2/3 + 3/6.
Step 4: Find a Common Denominator
To add these fractions, you need a common denominator. The denominators are 3 and 6. The least common multiple of 3 and 6 is 6. Convert 2/3 to a fraction with a denominator of 6. Multiply both the numerator and the denominator by 2: 2/3 = 4/6. Now, you have 1 + 4/6 + 3/6.
Step 5: Add the Fractions
Now, add the fractions with the common denominator. Combine 4/6 and 3/6: 4/6 + 3/6 = 7/6. So, you have 1 + 7/6.
Step 6: Simplify the Fraction
Notice that 7/6 is an improper fraction. Convert it to a mixed number. 7/6 is the same as 1 + 1/6. So, you have 1 + 1 + 1/6, which simplifies to 2 + 1/6.
Step 7: Final Answer
Combine the whole numbers and the fraction to get the final answer. The result is 2 and 1/6.
FAQs
Here are some frequently asked questions about subtracting mixed fractions:
1. How do you subtract mixed fractions step by step?
To subtract mixed fractions, follow these steps: 1. Convert mixed fractions to improper fractions. 2. Find a common denominator if needed. 3. Subtract the numerators while keeping the common denominator. 4. Simplify the result and convert back to a mixed fraction if necessary.
2. How do you borrow when subtracting mixed fractions?
When borrowing is needed: 1. Take 1 from the whole number part. 2. Convert this 1 to a fraction with the same denominator as the fractional part. 3. Add this to the existing fraction. 4. Proceed with the subtraction using the new mixed fraction.
3. How do you subtract mixed fractions using improper fractions?
To subtract using improper fractions: 1. Convert both mixed fractions to improper fractions. 2. Find a common denominator if needed. 3. Subtract the numerators while keeping the common denominator. 4. Simplify the result and convert back to a mixed fraction if desired.
4. How do you subtract mixed fractions with like denominators?
For mixed fractions with like denominators: 1. Subtract the whole numbers. 2. Subtract the fractions. 3. If borrowing is needed, take 1 from the whole number and add it to the fraction before subtracting. 4. Simplify the result if possible.
5. What are common mistakes when subtracting mixed fractions?
Common mistakes include: - Forgetting to find a common denominator for unlike denominators. - Incorrectly borrowing when needed. - Subtracting denominators instead of just numerators. - Forgetting to simplify the final answer. - Incorrectly converting between mixed and improper fractions.
Prerequisite Topics
Understanding the foundation of mathematics is crucial when tackling more complex concepts like adding and subtracting mixed numbers. To excel in this area, it's essential to grasp several key prerequisite topics that form the building blocks of this skill.
One fundamental concept to master is the negative exponent rule. While it may seem unrelated at first, understanding how to work with whole numbers and proper fractions is vital when dealing with mixed numbers. This knowledge helps in breaking down mixed numbers into their whole number and fractional components, making addition and subtraction more manageable.
Another critical skill is multiplying improper fractions and mixed numbers. This topic is particularly relevant because it involves simplifying improper fractions, a process often required when adding or subtracting mixed numbers. Being proficient in this area allows for smoother conversions between improper fractions and mixed numbers during calculations.
Perhaps the most directly related prerequisite is subtracting fractions with like denominators. This skill forms the core of subtracting mixed numbers, as you'll often need to perform this operation on the fractional parts. Mastering this concept ensures accuracy and efficiency when working with more complex mixed number problems.
Understanding greatest common factors (GCF) is also crucial. When adding or subtracting mixed numbers, you may need to simplify fractions or find a common denominator. Knowledge of GCF helps in identifying the least common multiple of denominators, which is essential for these operations.
Speaking of common denominators, proficiency in finding the least common multiple (LCM) is indispensable. This skill is particularly useful when adding or subtracting mixed numbers with different denominators. Understanding prime factorization for LCM allows you to quickly determine the common denominator needed for these operations.
By mastering these prerequisite topics, you'll build a strong foundation for adding and subtracting mixed numbers. Each concept contributes to your overall understanding and ability to perform these operations accurately and efficiently. Remember, mathematics is a cumulative subject, and investing time in these fundamental skills will pay dividends as you progress to more advanced topics. So, take the time to review and practice these prerequisites your future self will thank you when tackling complex mixed number problems becomes second nature!

