Theoretical vs. experimental probability
Topic Notes
In this lesson, we will learn:
- The difference between theoretical and experimental probability
- How to calculate the number of expected outcomes using theoretical probability and number of experimental trials
- How to write the experimental probability as a fraction based off the observed results in an experiment
Notes:
- Probability for simple events means we are just looking at one probability scenario at a time (i.e. one coin flip; a single six-sided die toss; one spinner)
- There are two types of probability:
- Theoretical probability is an educated guess on what you think should or will happen ("expected" probability; based on theory)
- Experimental probability is based on an experiment and what you saw happen already ("observed" probability; happened in reality)
- The probability we have seen so far in previous lessons is based on theoretical probability. We can use theoretical probability to find the number of expected outcomes.
- Before you do an experiment, you can predict how many times an outcome will happen (how many times it should theoretically happen)
(event) = - This is based on the number of trials you will do in the experiment. A trial is each run through of the experiment--1 trial will give 1 outcome (each coin flip, each dice toss, each spinner spin)
# expected outcomes = (event) × # trials - The experimental probability is based off the observations made during the experiment and calculated once all trials are completed.
(experimental event) =
Ex. For an experiment, a coin is flipped 8 times. The results are shown in an observation table:
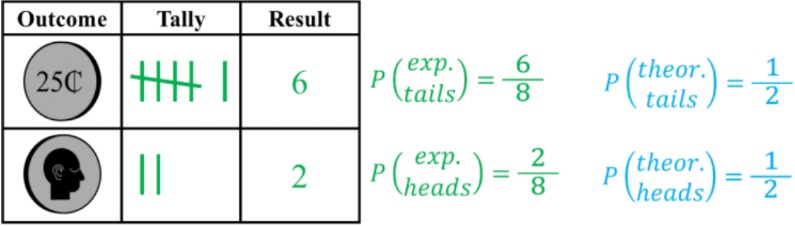
- The experimental (exp.) probabilities do not match with the theoretical (theor.) probabilities.
- The more trials you do, the closer the results should get to the expected probabilities (i.e. doing 10 trials vs. 100 trials vs. 1000 trials, etc.)
Introduction: Understanding Theoretical vs. Experimental Probability
Theoretical and experimental probability are two fundamental concepts in statistics that help us understand the likelihood of events occurring. Our introduction video provides a crucial foundation for grasping these concepts. Theoretical probability is based on logical reasoning and mathematical calculations, predicting outcomes without conducting experiments. It assumes ideal conditions and equal chances for all possible outcomes. On the other hand, experimental probability relies on actual data collected from repeated trials or observations. It reflects real-world results and can vary due to random factors. The main difference lies in their approach: theoretical probability is calculated beforehand, while experimental probability is determined after conducting experiments. Theoretical probability provides a baseline expectation, whereas experimental probability offers insights into practical outcomes. Understanding both types of probability is essential for making informed decisions in various fields, from science and engineering to finance and everyday life. By comparing theoretical and experimental probabilities, we can assess the accuracy of our predictions and identify potential biases or unexpected factors influencing outcomes.
Theoretical Probability: Predicting Outcomes
Theoretical probability is a fundamental concept in mathematics that allows us to predict the likelihood of events occurring based on logical reasoning and analysis. It is defined as the expected probability of an outcome, calculated using mathematical principles rather than empirical data. This approach provides a powerful tool for understanding and quantifying uncertainty in various situations.
At its core, theoretical probability is expressed as a ratio of favorable outcomes to the total number of possible outcomes, assuming all outcomes are equally likely. The formula for calculating theoretical probability is:
P(event) = (Number of favorable outcomes) / (Total number of possible outcomes)
This simple yet effective formula forms the basis for many probability calculations and predictions. Let's explore some common examples to illustrate how theoretical probability works in practice.
Consider a fair coin toss. There are two possible outcomes: heads or tails. The theoretical probability of getting heads is 1/2 or 0.5, as there is one favorable outcome (heads) out of two possible outcomes. The same applies to tails. This equal probability is why coin tosses are often used for fair decision-making.
Dice rolls provide another classic example of theoretical probability. A standard six-sided die has outcomes numbered from 1 to 6. The probability of rolling any specific number is 1/6, as there is one favorable outcome out of six possible outcomes. If we want to calculate the probability of rolling an even number, we have three favorable outcomes (2, 4, and 6) out of six possible outcomes, giving us a probability of 3/6 or 1/2.
Theoretical probability becomes particularly useful when we want to predict outcomes over multiple trials. To calculate expected outcomes, we use the formula:
Expected outcomes = P(event) × Number of trials
For instance, if we toss a fair coin 100 times, the expected number of heads would be 0.5 × 100 = 50. This doesn't mean we will always get exactly 50 heads in 100 tosses, but it provides a theoretical expectation based on probability.
Understanding theoretical probability is crucial in various fields, from statistics and data science to economics and decision-making. It allows us to make informed predictions, assess risks, and develop strategies based on logical analysis of possible outcomes. However, it's important to note that theoretical probability assumes ideal conditions, which may not always reflect real-world scenarios perfectly.
In practice, theoretical probability often serves as a starting point for more complex probability calculations. It can be combined with empirical data to refine predictions and account for real-world factors that might influence outcomes. This combination of theoretical and empirical approaches forms the basis of many statistical methods used in research, business, and everyday decision-making.
As we delve deeper into probability theory, we encounter more advanced concepts built upon the foundation of theoretical probability. These include conditional probability, which examines the likelihood of an event occurring given that another event has already occurred, and Bayes' theorem, which allows us to update probabilities based on new information.
In conclusion, theoretical probability provides a powerful framework for understanding and predicting outcomes in uncertain situations. By applying logical reasoning and mathematical principles, we can calculate the likelihood of events, make informed decisions, and develop strategies to navigate complex scenarios. Whether you're analyzing game strategies, assessing investment risks, or conducting scientific research, a solid grasp of theoretical probability is an invaluable tool in your analytical toolkit.
Experimental Probability: Observing Real Results
Experimental probability is a fundamental concept in statistics that refers to the observed probability of an event based on actual experiments or trials. Unlike theoretical probability, which is calculated mathematically, experimental probability is derived from real-world observations and can provide valuable insights into the likelihood of various outcomes.
To understand experimental probability, let's consider a simple experiment: flipping a coin. While the theoretical probability of getting heads or tails is 0.5 (or 50%) each, the actual results may vary when we conduct the experiment. Here's how to perform this experiment and record the results:
- Choose a fair coin and decide on the number of flips (e.g., 100 flips).
- Flip the coin and record each outcome using tally marks. Create two columns: one for heads and one for tails.
- After completing all flips, count the total number of heads and tails.
Tally marks are an efficient way to keep track of results during probability experiments. They allow for quick and easy counting in groups of five, making it simple to tally large numbers of trials.
Once you have your results, you can calculate the experimental probability using this formula:
Experimental Probability = (Number of observed outcomes) / (Total number of trials)
For example, if you flipped heads 48 times out of 100 flips, the experimental probability of getting heads would be:
Experimental Probability (Heads) = 48 / 100 = 0.48 or 48%
It's important to note that experimental probability may not always match the theoretical probability exactly, especially with a small number of trials. As you increase the number of trials, the experimental probability tends to converge towards the theoretical probability. This phenomenon is known as the Law of Large Numbers.
Comparing experimental results with theoretical expectations can be enlightening. In our coin flip example, you might find that your experimental probability is close to, but not exactly, 50% for heads and tails. This difference can spark discussions about factors that might influence the results, such as:
- The fairness of the coin
- The flipping technique
- Environmental factors (e.g., wind)
- The number of trials conducted
Experimental probability has numerous real-world applications. Scientists use it to test hypotheses, businesses employ it for market research, and it's crucial in fields like quality control and risk assessment. By conducting probability experiments and analyzing the results, we can gain valuable insights into the likelihood of various outcomes in different scenarios.
To further explore experimental probability, consider conducting experiments with other random events, such as:
- Rolling dice and recording the outcomes
- Drawing cards from a deck and noting the suits or values
- Spinning a spinner and tracking where it lands
In conclusion, experimental probability offers a practical approach to understanding the likelihood of events through observation and experimentation. By conducting simple experiments, recording results with tally marks, and calculating probabilities, we can compare real-world outcomes with theoretical expectations. This process not only enhances our understanding of probability but also develops critical thinking skills and an appreciation for the role of data collection and analysis in decision-making.
Comparing Theoretical and Experimental Probability
Understanding the differences between theoretical and experimental probability is crucial in the field of statistics and probability theory. The coin flip example from the video provides an excellent illustration of these concepts. Theoretical probability is based on mathematical calculations and assumes ideal conditions, while experimental probability is derived from actual observations and trials.
In the case of a fair coin flip, the theoretical probability of getting heads or tails is exactly 50% or 0.5 for each outcome. This is because there are only two possible outcomes, and each is equally likely to occur. However, when we conduct actual coin flips, the experimental results may not always match these theoretical expectations.
There are several reasons why experimental results can deviate from theoretical probabilities. First, real-world conditions are rarely perfect. Factors such as the coin's weight distribution, air resistance, or the flipping technique can introduce slight biases. Additionally, random chance plays a significant role, especially in smaller sample sizes.
For instance, if we flip a coin 10 times, it's not uncommon to see results like 7 heads and 3 tails, which appears to deviate significantly from the expected 50-50 split. This deviation doesn't necessarily mean the coin is unfair or the theoretical probability is incorrect. It's simply a result of the limited number of trials.
This is where the importance of increasing the number of trials comes into play. As we increase the sample size, the experimental results tend to converge towards the theoretical probability. This phenomenon is known as the Law of Large Numbers. With a larger number of coin flips, say 1000 or 10,000, the proportion of heads to tails is likely to be much closer to the expected 50-50 ratio.
Increasing the number of trials helps to minimize the impact of random fluctuations and short-term variations. It allows for a more accurate representation of the underlying probability distribution. In our coin flip example, as we approach an infinite number of flips, the experimental probability would theoretically converge exactly to the 50% mark for both heads and tails.
This principle of convergence through increased trials applies not just to coin flips but to various probabilistic scenarios in statistics, science, and everyday life. It underscores the importance of large sample sizes in research and data analysis to draw reliable conclusions.
In conclusion, while theoretical and experimental probabilities may differ in small-scale experiments, increasing the number of trials brings experimental results closer to theoretical expectations. This comparison between theoretical and experimental probability highlights the dynamic nature of probability and the critical role of sample size in statistical analysis.
Applications of Theoretical and Experimental Probability
Theoretical and experimental probability play crucial roles in various real-world applications, offering valuable insights across multiple fields. In statistics, these concepts form the foundation for data analysis and prediction models. For instance, in medical research, theoretical probability helps calculate the likelihood of a drug's effectiveness based on its chemical composition, while experimental probability is derived from clinical trials, providing actual success rates.
In the realm of science, weather forecasting exemplifies the interplay between theoretical and experimental probability. Meteorologists use complex mathematical models (theoretical probability) to predict weather patterns, but they also rely on historical data and real-time observations (experimental probability) to refine their forecasts. This combination leads to more accurate predictions of severe weather events, helping communities prepare and potentially saving lives.
The insurance industry heavily relies on probability applications. Actuaries use theoretical probability to assess risk factors and set premiums for various insurance policies. However, they also analyze claim data (experimental probability) to adjust their models and ensure fair pricing. This balance between theory and real-world data helps insurance companies maintain profitability while offering competitive rates to customers.
In the field of quality control, manufacturers use theoretical probability to estimate defect rates in production processes. Simultaneously, they conduct random sampling (experimental probability) to verify and adjust these estimates. This approach helps maintain product quality and optimize manufacturing efficiency.
Decision-making in business often involves probability applications. For example, in marketing, companies use theoretical probability to estimate the success rate of a new product based on market research. They then conduct limited releases or A/B testing (experimental probability) to gather real-world data before full-scale launches. This strategy minimizes risks and maximizes the potential for success in competitive markets.
The gaming and gambling industries are built on probability concepts. Casino games are designed using theoretical probability to ensure a house edge, while player experiences represent experimental probability. Understanding both aspects is crucial for players to make informed decisions and for casinos to maintain profitability.
In conclusion, the synergy between theoretical and experimental probability enhances our ability to make accurate predictions and informed decisions across various fields. By combining mathematical models with real-world data, we can develop more robust strategies in science, business, and everyday life. This comprehensive approach to probability leads to better risk assessment, more effective problem-solving, and improved outcomes in countless applications.
Common Misconceptions and Pitfalls
Probability is a fundamental concept in mathematics and statistics, yet it's often misunderstood. Many people fall prey to common misconceptions about theoretical probability and experimental probability, leading to flawed decision-making and incorrect interpretations of data. In this section, we'll address these misconceptions and provide tips on how to avoid misinterpreting probability results in various scenarios.
One of the most prevalent misconceptions is the gambler's fallacy. This is the erroneous belief that if an event has occurred more frequently than normal in the past, it's less likely to happen in the future (or vice versa). For example, if a coin has landed on heads several times in a row, some might believe that tails is "due" to come up next. However, each coin flip is an independent event, and the probability of getting heads or tails remains 50% regardless of past outcomes.
Another important concept to understand is the law of large numbers. This principle states that as the number of trials increases, the experimental probability will converge to the theoretical probability. However, many people misinterpret this law, believing that a small number of trials is sufficient to accurately represent the true probability. In reality, a large sample size is often necessary to obtain reliable results.
To avoid misinterpreting probability results, it's crucial to consider the sample size and context of the data. Small samples can lead to misleading conclusions, as they may not accurately represent the population. Additionally, it's important to recognize that correlation does not imply causation. Just because two events occur together doesn't mean one causes the other.
When dealing with probability, it's also essential to understand the concept of independent events. Many people assume that past events influence future outcomes in situations where events are actually independent. This can lead to poor decision-making, especially in gambling or financial contexts.
To improve your understanding of probability, consider the following tips: First, always question your assumptions and look for potential biases. Second, use large sample sizes whenever possible to get more accurate results. Third, be aware of the gambler's fallacy and avoid making predictions based on past outcomes in independent events. Finally, educate yourself on basic statistical concepts and probability theory to better interpret data and make informed decisions.
By addressing these common misconceptions and following these tips, you can develop a more accurate understanding of probability and avoid falling into common pitfalls. This knowledge will serve you well in various fields, from scientific research to everyday decision-making.
Conclusion: Bridging Theory and Practice in Probability
In summarizing probability concepts, it's crucial to understand the key differences between theoretical and experimental probability. Theoretical probability is based on logical analysis and mathematical calculations, while experimental probability relies on actual observations and data collection. Both approaches are essential for accurate probability analysis. Theoretical probability provides a foundation for predicting outcomes, while experimental probability offers real-world validation. By grasping these concepts, you can apply probability theory to various aspects of your studies and daily life, from statistical analysis to decision-making. Remember that theoretical predictions may not always align perfectly with experimental results due to real-world factors. To reinforce your understanding, we encourage you to revisit the introduction video, which provides a visual explanation of these concepts. By mastering both theoretical and experimental probability, you'll develop a more comprehensive and practical approach to probability analysis, enhancing your problem-solving skills in various fields.
Introduction to Basic Probability for Simple Events: Theoretical Probability and Expected Outcomes
In this guide, we will explore the concepts of theoretical and experimental probability, focusing on understanding theoretical probability and expected outcomes. This will help you build a solid foundation in basic probability for simple events.
Step 1: Understanding Theoretical Probability
Theoretical probability is the type of probability that is based on theoretical reasoning and logic. It involves predicting what might happen based on known information and logical deduction. Theoretical probability is calculated using the formula:
Probability of an event (P) = Number of favorable outcomes / Total number of possible outcomes
For example, when flipping a coin, there are two possible outcomes: heads or tails. The probability of getting heads is 1 out of 2, or 1/2.
Step 2: Understanding Experimental Probability
Experimental probability, on the other hand, is based on actual experiments and observations. It involves conducting an experiment and recording the outcomes to determine the probability of an event. Experimental probability is calculated using the formula:
Experimental Probability (P) = Number of times an event occurs / Total number of trials
For instance, if you flip a coin 10 times and it lands on heads 6 times, the experimental probability of getting heads is 6/10 or 0.6.
Step 3: Differences Between Theoretical and Experimental Probability
The main difference between theoretical and experimental probability is that theoretical probability is based on logical reasoning and predictions, while experimental probability is based on actual observations and experiments. Theoretical probability is what we expect to happen, whereas experimental probability is what actually happens in practice.
Step 4: Calculating Theoretical Probability
To calculate theoretical probability, you need to determine the number of favorable outcomes and the total number of possible outcomes. For example, in a coin toss, there are two possible outcomes (heads or tails), and each outcome is equally likely. Therefore, the theoretical probability of getting heads is:
P(Heads) = 1 (favorable outcome) / 2 (total possible outcomes) = 1/2
Step 5: Expected Outcomes
Expected outcomes refer to the number of times an event is predicted to occur based on its theoretical probability. The formula for calculating expected outcomes is:
Expected Outcomes = Probability of an event (P) × Number of trials
For example, if you flip a coin 8 times, the expected number of times it will land on heads can be calculated as follows:
Expected Outcomes = P(Heads) × Number of trials = 1/2 × 8 = 4
This means that if you flip a coin 8 times, you can expect it to land on heads 4 times.
Step 6: Applying the Expected Outcomes Formula
To apply the expected outcomes formula, follow these steps:
- Determine the probability of the event (P).
- Identify the number of trials (N).
- Multiply the probability of the event by the number of trials to get the expected outcomes.
For example, if you want to know how many times a coin will land on heads if flipped 8 times, you would use the formula:
Expected Outcomes = 1/2 × 8 = 4
This means you can expect the coin to land on heads 4 times out of 8 flips.
Step 7: Understanding Trials
In probability experiments, a trial refers to each individual instance of conducting the experiment. For example, each time you flip a coin is considered one trial. The total number of trials is the number of times you repeat the experiment. In the coin flip example, if you flip the coin 8 times, you have conducted 8 trials.
Step 8: Practical Example
Let's go through a practical example to solidify our understanding of expected outcomes. Suppose you flip a coin 8 times and want to know how many times it should land on heads. Using the expected outcomes formula:
Expected Outcomes = P(Heads) × Number of trials = 1/2 × 8 = 4
This means that out of 8 coin flips, you can expect the coin to land on heads 4 times. This is based on the theoretical probability that the coin has an equal chance of landing on heads or tails.
Conclusion
Understanding theoretical and experimental probability is essential for predicting and analyzing outcomes in various scenarios. Theoretical probability helps us make predictions based on logic and known information, while experimental probability provides insights based on actual observations. By using the expected outcomes formula, we can estimate the number of times an event is likely to occur based on its theoretical probability and the number of trials conducted.
FAQs
-
What is the difference between theoretical and experimental probability?
Theoretical probability is calculated mathematically based on logical reasoning and assumes ideal conditions. It predicts outcomes without conducting experiments. Experimental probability, on the other hand, is derived from actual data collected through repeated trials or observations. It reflects real-world results and can vary due to random factors.
-
How do you calculate theoretical probability?
Theoretical probability is calculated using the formula: P(event) = (Number of favorable outcomes) / (Total number of possible outcomes). For example, the theoretical probability of rolling a 6 on a fair six-sided die is 1/6, as there is one favorable outcome out of six possible outcomes.
-
Why might experimental probability differ from theoretical probability?
Experimental probability may differ from theoretical probability due to various factors such as random chance, imperfect experimental conditions, or a limited number of trials. Real-world conditions are rarely ideal, and factors like slight biases in equipment or environmental influences can affect outcomes.
-
What is the Law of Large Numbers in probability?
The Law of Large Numbers states that as the number of trials in an experiment increases, the experimental probability tends to converge towards the theoretical probability. This principle explains why larger sample sizes generally provide more accurate representations of true probabilities.
-
How can understanding probability concepts be applied in real life?
Understanding probability concepts has numerous real-life applications, including: - Making informed decisions in business and finance - Assessing risks in insurance and healthcare - Improving quality control in manufacturing - Enhancing strategies in games and sports - Interpreting scientific research and statistical data These concepts help in predicting outcomes, evaluating chances, and making more rational choices in uncertain situations.
Prerequisite Topics for Understanding Theoretical vs. Experimental Probability
When delving into the fascinating world of theoretical vs. experimental probability, it's crucial to have a solid foundation in several key concepts. Understanding these prerequisite topics will greatly enhance your ability to grasp the nuances between theoretical predictions and real-world outcomes.
One of the fundamental concepts you should master is the probability of independent events. This concept forms the backbone of many probability calculations and is essential when comparing theoretical and experimental probabilities. By understanding how to calculate the likelihood of multiple events occurring independently, you'll be better equipped to predict outcomes in both theoretical models and practical experiments.
Another critical prerequisite is conditional probability. This concept becomes particularly relevant when examining the relationship between theoretical and experimental probabilities in real-world scenarios. Conditional probability helps you understand how the occurrence of one event can influence the probability of another, which is often a key factor in explaining discrepancies between theoretical predictions and experimental results.
Lastly, a solid grasp of influencing factors in data collection is crucial when exploring theoretical vs. experimental probability. Understanding how various factors can affect the data collection process is vital for interpreting experimental results accurately and comparing them to theoretical predictions. This knowledge helps you identify potential sources of bias or error that might lead to differences between expected and observed probabilities.
By mastering these prerequisite topics, you'll be well-prepared to tackle the complexities of theoretical vs. experimental probability. The probability of independent events provides the mathematical foundation for making predictions, while conditional probability helps you account for real-world dependencies. Understanding the influencing factors in data collection ensures that you can critically evaluate experimental results and their relationship to theoretical models.
As you explore the differences between theoretical and experimental probability, you'll find that these prerequisite concepts continually come into play. They will help you understand why theoretical predictions might differ from experimental outcomes, how to account for various factors that influence probability in real-world situations, and how to design experiments that can effectively test theoretical models.
Remember, the journey to fully grasping theoretical vs. experimental probability is built upon these fundamental concepts. By investing time in understanding these prerequisites, you'll develop a more comprehensive and nuanced understanding of probability theory and its practical applications. This knowledge will not only enhance your academic performance but also equip you with valuable skills for analyzing and interpreting probabilistic events in various fields, from statistics and science to finance and decision-making.

