Fundamental counting principle
Combinatorics is a branch of math that focuses on calculating total amounts of possible outcomes for a certain combination of events, or item categories which are finite and obey certain conditions. Combinations and permutations are usually the main topics of study in this subject, but the basis for both starts with something denominated in the fundamental counting principle.
And so, in order to provide a deep introduction to combinatorics we start this chapter on our statistics course by studying what this fundamental principle is.
What is the fundamental counting principle?
The fundamental counting principle is a tool that helps us figure out the total possible outcomes of a combination of multiples events in a time-effective manner. In other words, if we have two or more different events (or categories) where each of them has a variety of possible outcomes occurring either at the same time, or in combination in order to produce a result, the fundamental counting principle provides a rapid manner of literally counting every single possible combination of outcomes from the combined events.
The basis of the counting principle can be easily explained with a tree diagram.
Let us look at a simple example of this: Imagine you go to a dessert bar and have a choice between eating cake or ice cream, besides that you know that the establishment offers 3 different kinds of each (cake and ice-cream), therefore you end up with the categories of:
Types of dessert: cake and ice cream (2 types)
Flavors of each dessert type: for cake = cheesecake, carrot cake, chocolate cake; for ice cream = vanilla, strawberry, chocolate (3 flavors each).
If you are eating only one, how many different desert options do you have to choose from? Let us make a tree diagram to find out:
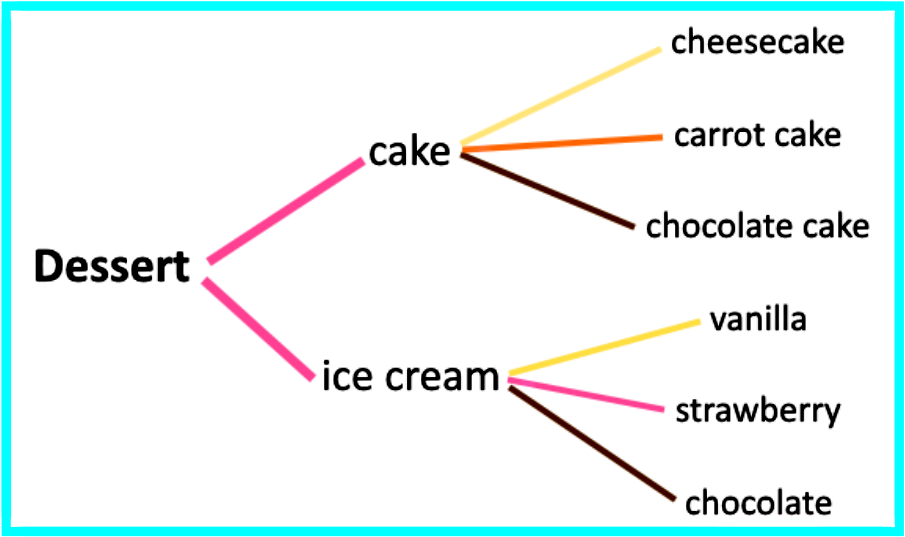
For this example we can clearly see that there are 6 different possibilities on the dessert you will end up enjoying, but imagine if there were many more options besides just cake and ice cream, and what if these other types of desserts had their own multiple options? We could still continue to count the different possible outcomes by drawing tree diagrams but these would get bigger and bigger, and even more difficult to manage.
Thus, we define fundamental counting principle to solve for those processes!
This principle uses the multiplication of the possible outcomes of simultaneous combined events in order to produce the total amount of outcome combinations that can result from such events happening at the same time or needed for a certain process (you know, the events do not necessarily need to occur at exactly the same moment, but they need to occur for the particular desired process to yield a result).
In simple words, the fundamental counting principle says that: "If there are m possible ways for an event to occur, and n possible ways for another event to occur, then there are possible ways for both events to occur".
Where is the amount of possible outcomes of the first event, and n is the amount of possible outcomes of the second event. For the case in which you want to know the possible desserts you can choose from, the first event is defined as the type of dessert you can pick (either cake or ice cream) where = 2, and then the second event is the amount of possible options each of them have (for this case = 3). Then you just multiply = 2 × 3 = 6 and you obtain the six possible options you have to choose from dessert at that dessert bar!
You can expand the counting principle to contain as many events as deemed necessary in a situation, just continue to multiply the amount of possible outcomes for each category and you will obtain the total amount of possible combinations that can result.
Therefore, when solving fundamental counting principle problems you need to take a look at the amount of possible outcomes for each event or category (depending what the problem is all about) and then multiply the amount of possible outcomes of each of these events in order to find the total amount of possible outcome combinations.
Fundamental counting principle examples
To show in detail how the principle of counting works, let us take a look at a few example problems:
Example 1
You are packing clothes for a trip. You decide to take three shirts and two pairs of pants:
Shirts: tank top, short sleeve, long sleeve
Pants: skinny jeans, baggy pants
a) How many pieces of clothing are you bringing all together?
5 pieces of clothing, since is three shirts plus two pair of pants.
a) If an outfit consists of a shirt and a pair of pants, how many different sets of outfit can you make? Determine the answer by using:
(i) a tree diagram
Remember that in order to make a tree diagram we need to pick a category of the given items, and list them. Then, for each of the items in the first category we will draw a total of branches containing the whole next category. If another category exists, then to each of the already made branches we will extend the total amount of branches for the next category and this same process gets repeated as long as another category exists.
For this particular case, we have two categories: shirts and pants. There are a total of three shirts and two pairs of pants; therefore, we list the items contained in the shirts category first, and then, to each of these items we draw two branches, each representing one item from the pants category. The tree diagram that results from this look as follows:
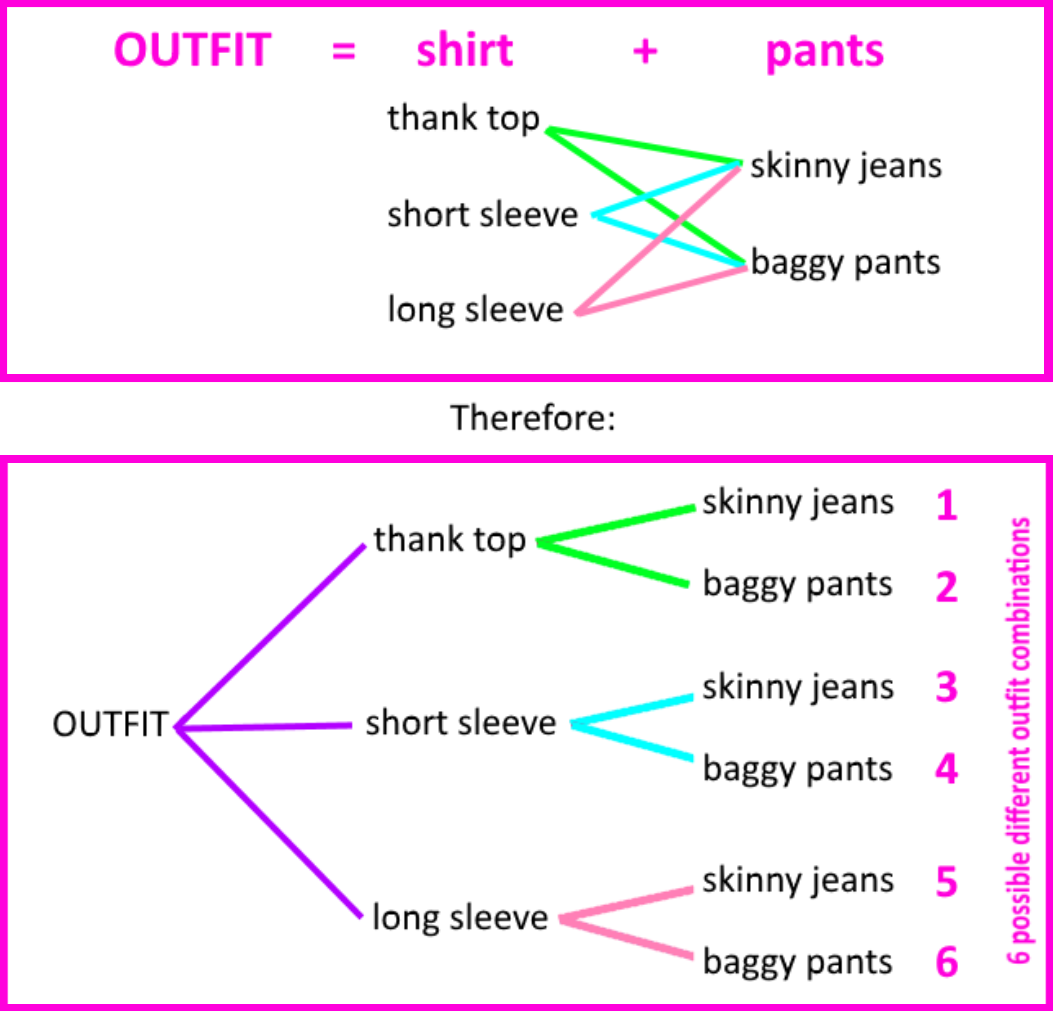
(ii) the fundamental counting principle
Using the fundamental principle of counting, we know that for m possible ways for an event to occur, and n possible ways for another event to occur, there are m x n possible ways for both events to occur.
Analyzing this case:
Since we have 3 shirts, that means that we have a total of three possible options for a certain shirt to be worn in your outfit, and so, the first event is the shirt category, where m equals 3 (being = 3 possible shirts to be worn). The second possible event to occur in the type of pants that can be work in the outfit, and therefore, there are two possible ways because you packed 2 different pair of pants, and so =2.
To obtain the total possible sets of shirt with pants in an outfit that you may wear, we use the fundamental counting principle formula defined above and multiply the values of m and n, we obtain: = 3 2 = 6. And so, there are 6 possible different outfits for the 5 pieces of clothing packed.
Example 2
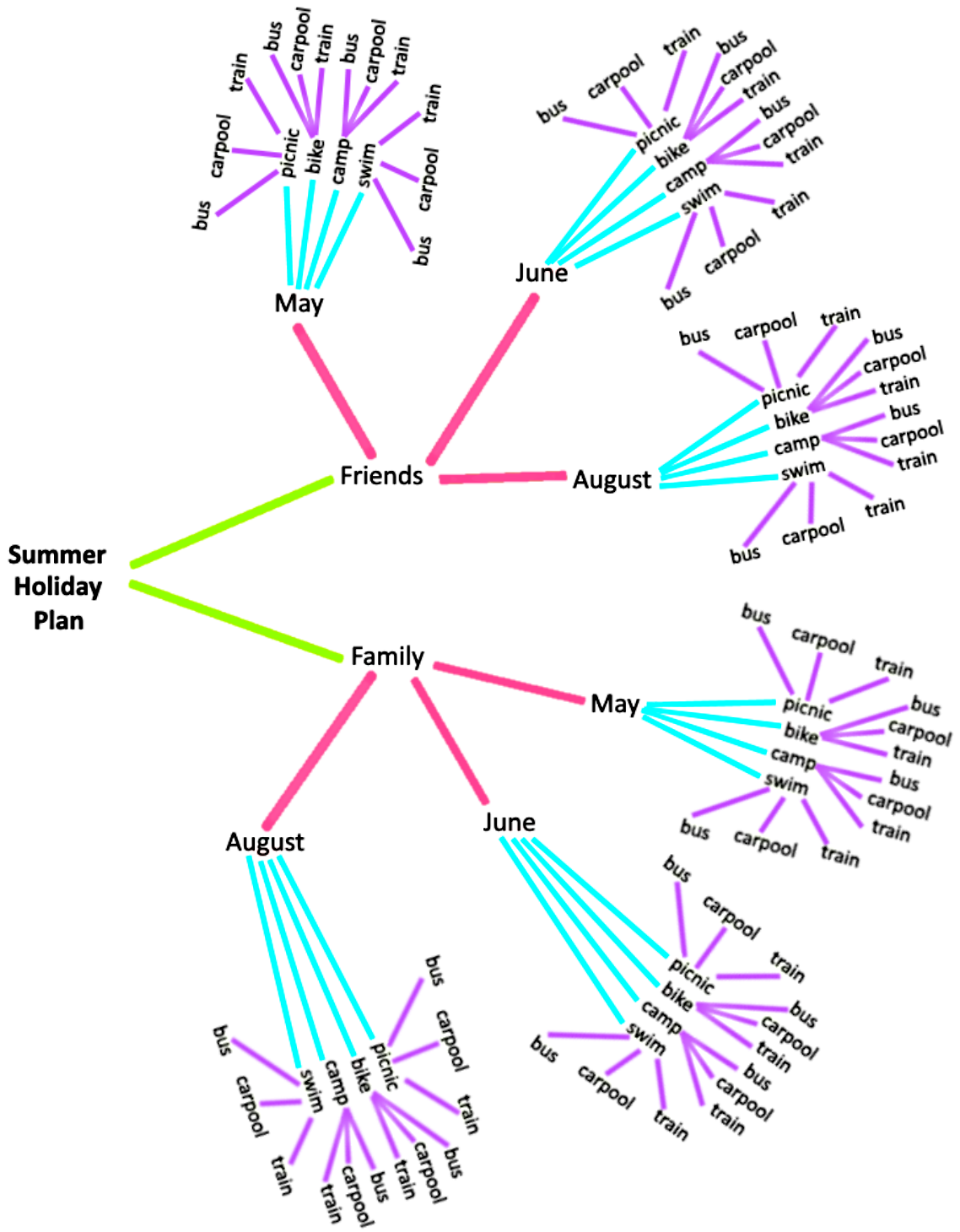
A summer holiday plan has one item from each category:
Companion: friends, family
Month: May, June, August
Activities: picnic, bike, camp, swim
Transportation: bus, carpool, train
How many different summer holiday plans are possible?
Using the fundamental counting principle definition we observe the item quantity in each category and then multiply these amounts to obtain the total amount of different summer holiday plans possible:
Companion = 2 possible options
Month = 3 possible options
Activities = 4 possible options
Transportation = 3 possible options
And so, we multiply to obtain the total amount of different plan sets for the summer holiday:
2 × 3 × 4 × 3 = 72. Therefore, there are 72 different ways in which the summer holiday can be enjoyed.
Drawing the tree diagram for this problem, we have that:
Example 3
A survey has ten multiple choice questions. There are four choices in each question, , , , or . How many different possible sets of answers are there?
For this case, we check into the possible answers for each of the questions in the survey, let us build a table so you can see this:
|
Questions |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Possible Answers |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
Therefore, using the fundamental principle of counting we multiply the possible outcome of each question so we can obtain a final amount of the total answer combinations that can result from such survey:
This particular problem gives us insight in how complicated statistics can get when trying to take into account every single characteristic and answer from a population; just imagine, if you were to give a small survey of ten questions to a group of people where each question has four possible answers, you end up with 1048576 possible different responses!!! At this point, statistics analysis of every category (each question) would probably be better than trying to correlate the ten different categories (questions) in a single report (is doable, but much more extensive than comparing the statistics per each question).
Example 4
Using only the digits 2, 4, 5, 6, 7, 8 and 9 to produce four digit numbers.
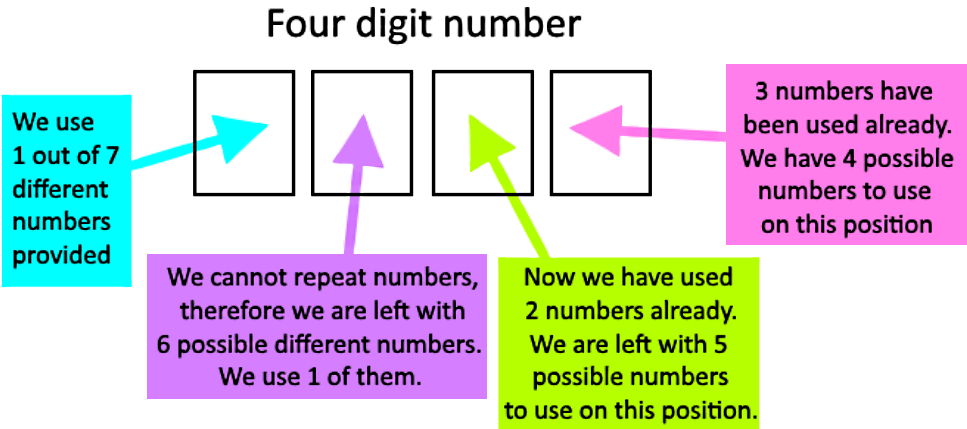
Then, in order to know how many four digit numbers can be constructed with the set of numbers provided, we construct the number digit by digit:
- The total amount of possible numbers to use is 7, the set of 7 numbers to use is: 2, 4, 5, 6, 7, 8 and 9.
- We have four space positions to fill up with those digits, in the first space we have 7 different possible numbers to use, since those are the notal possible numbers we were provided with.
- Then to fill up the next space, since we cannot repeat the number we used in the first space, we have only 6 options left for that second space position.
- The same goes to the third space position, since we have already used two numbers, we are left with only 5 possible digits we can use in the third space position. And for the fourth position space we have only 4 possible numbers left since we have already used 3. This looks like:
- Thus, following the fundamental counting principle we multiply the possibility amounts for each position space and obtain the total amount of combinations possible to construct a 4 digit number with the restrictions given:
(i) even?
Once more, we construct the 4-digit number by each space position, but in this case, we start by looking at the possible digits that can be used in the fourth space given the restrictions.
- Out of the seven provided numbers, only 4 are even, one of these even numbers MUST be the fourth digit in the constructed number. Therefore, the fourth position space has 4 possible options.
- Then we fill up the other space positions: Since we already used one number in the fourth position, the first position has a total of 6 different options, then the second has a total of 5 possible options, and the third one has a total of 4 different options.
- We multiply these options per space position and obtain the total amount of possible combinations that will result in an even 4-digit number:
(ii) odd?
This one is very simple, since we have a total of 840 possible different 4-digit numbers constructed with the digits provided, and 480 of them are even, then the rest of them is odd, and so:
(iii) multiples of 5?
On this case, we have a similar case as for the even numbers, but given the 7 digits that we can use to construct the 4-digit number, the only way this number is multiple of 5 is when it ends in 5 (since there is no zero in the possible options). Therefore, the fourth space position of the 4-digit number has only one possible digit in there.
Filling up the rest spaces: the first position has a total of 6 different options (since we already used number 5 on the fourth position), then the second has a total of 5 possible options, and the third one has a total of 4 different options:
(iv) more than 3000?
To be bigger than 3000 it means the first digit on our resulting number must be either 3 or higher. 6 out of our 7 provided numbers meet that condition and so, the first digit has 6 possible options.
Then we fill up the rest of them as we have done before: the second position has a total of 6 different options (since we already used a number on the first position), then the third has a total of 5 possible options, and the fourth one has a total of 4 different options:
Having worked through some fundamental counting principles examples, let us finalize this lesson with a few suggestions that may be of aid to your independent studies: on this article on counting principles there is an introduction to our topic of today and then an expansion into concepts coming up in our next lessons (permutations and combinations). Then we have this book excerpt completely dedicated to the the fundamental counting principle where the topic is explained and contains several other examples that we recommend you to work through.
This is it for our lesson of today, see you in the next one where we will make the comparison of permutation vs combination, get ready for some combinatorics!






