Pairs of lines and angles
Topic Notes
Introduction to Parallel Lines and Transversals
Welcome to our exploration of parallel lines and transversals! This fascinating topic is a cornerstone of geometry, and I'm excited to guide you through it. We'll start with a brief introduction video that sets the stage for our learning journey. This video is crucial as it visually demonstrates the key concepts we'll be discussing. Parallel lines, as you'll see, are lines that never intersect no matter how far they extend. A transversal is a line that crosses these parallel lines, creating interesting angle relationships. As we delve deeper, you'll discover how these angles relate to each other, forming patterns that are both beautiful and mathematically significant. Understanding these relationships is essential for solving more complex geometric problems. So, let's dive in and unravel the mysteries of parallel lines and transversals together! Remember, this knowledge will be a powerful tool in your mathematical toolkit.
Understanding Parallel Lines and Their Properties
Parallel lines are a fundamental concept in geometry and algebra, playing a crucial role in various mathematical applications. Imagine a set of train tracks stretching into the distance - this is a perfect real-world example of parallel lines. Just as train tracks never meet, parallel lines are defined as two or more lines in the same plane that never intersect, no matter how far they are extended.
The key characteristics of parallel lines include:
- Constant distance: The perpendicular distance between parallel lines remains the same at all points.
- No intersection: Parallel lines will never cross or meet, even if extended infinitely.
- Same slope: In a coordinate plane, parallel lines always have the same slope.
The concept of parallel lines is closely related to linear equations. In algebra, a linear equation represents a straight line on a coordinate plane. When two linear equations have the same slope but different y-intercepts, they represent parallel lines. This relationship between parallel lines and linear equations is crucial in solving many geometric and algebraic problems.
Slopes play a vital role in understanding parallel lines. The slope of a line is a measure of its steepness, calculated as the change in y-coordinates divided by the change in x-coordinates between two points on the line. For parallel lines, this slope is identical. Using our train track analogy, imagine the tracks climbing a hill - both rails would ascend at the same rate, maintaining their parallel nature.
In mathematical terms, if two lines have equations y = mx + b1 and y = mx + b2, where m is the slope and b1 and b2 are different y-intercepts, these lines are parallel. The identical 'm' value ensures they maintain the same angle with respect to the x-axis, never converging or diverging.
Visualizing parallel lines in geometry problems can greatly aid in understanding and solving them. Here are some tips for visualization:
- Draw the lines: Sketch the lines on graph paper or a coordinate plane to see their relationship visually.
- Use a straightedge: Ensure the lines are perfectly straight to maintain their parallel nature.
- Extend the lines: Mentally or physically extend the lines to reinforce that they never intersect.
- Check the distance: Measure the perpendicular distance between the lines at different points to confirm it remains constant.
Understanding parallel lines is essential in various fields beyond mathematics. In architecture and engineering, parallel lines are used in designing structures and ensuring proper alignment. In computer graphics, they play a role in creating perspective and 3D models. Even in everyday life, we encounter real-world examples of parallel lines in road markings, building designs, and various geometric patterns.
To further solidify your understanding, consider practicing problems that involve finding equations of parallel lines, determining if given lines are parallel, and solving real-world problems that utilize the concept of parallel lines. Remember, just like those train tracks running side by side into the horizon, parallel lines maintain their steady, unchanging relationship, embodying a fundamental principle of geometry that extends far beyond the classroom into the world around us.
Transversals and Angle Relationships
In geometry, transversals play a crucial role in understanding the relationships between lines and angles. A transversal is a line that intersects two or more other lines at distinct points. When a transversal crosses parallel lines, it creates a fascinating set of angle relationships that are fundamental to geometric proofs and problem-solving.
When a transversal intersects two parallel lines, it forms eight angles. These angles can be categorized into four pairs of corresponding angles, four pairs of alternate interior angles, four pairs of alternate exterior angles, and two pairs of consecutive interior angles. Understanding these angle relationships is key to mastering geometric concepts.
The eight angles created by a transversal intersecting two parallel lines are:
- Four exterior angles (located outside the parallel lines)
- Four interior angles (located between the parallel lines)
These angles have special relationships:
- Corresponding angles are congruent (equal in measure)
- Alternate interior angles are congruent
- Alternate exterior angles are congruent
- Consecutive interior angles are supplementary (add up to 180 degrees)
Supplementary angles are a crucial concept in geometry. Two angles are considered supplementary when their measures add up to 180 degrees. This relationship is closely tied to straight lines, as the angles on a straight line always sum to 180 degrees. Supplementary angles don't need to be adjacent; they can be found in various configurations, including those created by transversals.
In the context of transversals and parallel lines, consecutive interior angles are always supplementary. This property is often used in geometric proofs and problem-solving. For example, if you know the measure of one interior angle, you can easily calculate its supplementary pair by subtracting from 180 degrees.
Another important concept in angle relationships is that of vertically opposite angles, also known as the x-angle rule. When two lines intersect, they form four angles. The angles directly opposite each other are called vertically opposite angles. The x-angle rule states that vertically opposite angles are always congruent, meaning they have the same measure.
The x-angle rule applies to any intersecting lines, not just transversals and parallel lines. It's a fundamental property that holds true regardless of whether the intersecting lines are perpendicular, parallel, or neither. This rule is named after the "X" shape formed by the intersecting lines and the congruent angles.
To visualize the x-angle rule, imagine drawing an "X" and labeling the four angles created at the intersection. The angles at the top and bottom of the "X" are congruent, as are the angles on the left and right sides. This property is extremely useful in solving geometric problems and proving theorems about intersecting lines.
When applying the x-angle rule to transversals intersecting parallel lines, we can see that it works in conjunction with the other angle relationships. For instance, the vertically opposite angles formed by the transversal are congruent, and these angles also correspond to angles formed where the transversal intersects the other parallel line.
Understanding these angle relationships - supplementary angles, vertically opposite angles, and the various pairs formed by transversals intersecting parallel lines - is essential for success in geometry. These concepts form the foundation for more advanced topics and are frequently used in geometric proofs and real-world applications.
In conclusion, transversals, supplementary angles, and vertically opposite angles are interconnected concepts that provide a framework for understanding the geometry of intersecting lines. By mastering these relationships, students can develop strong problem-solving skills and gain a deeper appreciation for the elegant symmetry inherent in geometric structures.
Corresponding Angles and F-Angle Relationships
Let's dive into the fascinating world of corresponding angles and the F-angle relationship! These concepts are essential in geometry and can help us prove angle equality in various situations. We'll break it down step-by-step to make it easy to understand.
First, let's define corresponding angles. When two lines are crossed by a transversal (a line that intersects two or more other lines), corresponding angles are formed. These angles appear in the same relative position at each intersection point. They're like twins, mirroring each other's position!
Now, here's where it gets interesting: corresponding angles are always equal. This property is fundamental in geometry and leads us to the F-angle relationship.
The F-angle relationship is a clever way to remember how corresponding angles work. Imagine drawing the letter "F" using the lines in your geometric figure. The two horizontal lines of the "F" represent the parallel lines, while the vertical line represents the transversal. The angles formed at the intersections of these lines create our corresponding angles.
Here's how to use the F-angle relationship to identify corresponding angles:
- Look for two parallel lines crossed by a transversal.
- Mentally draw an "F" shape using these lines.
- The angles at the "tips" of the F are corresponding angles.
- Remember, these angles will always be equal!
Let's explore some examples to solidify our understanding:
Example 1: Imagine two horizontal parallel lines crossed by a diagonal transversal. The top-left angle corresponds to the bottom-left angle on the lower line. These angles form the "tips" of our mental F-shape and are equal.
Example 2: Now, picture two vertical parallel lines crossed by a horizontal transversal. The upper-right angle on the left line corresponds to the upper-left angle on the right line. Again, these form the tips of our F and are equal.
The beauty of the F-angle relationship is that it works regardless of the orientation of the lines. Whether your parallel lines are horizontal, vertical, or slanted, the F-shape will help you identify those corresponding angles.
Why is this important? The F-angle relationship and corresponding angles are powerful tools in geometric proofs. When you need to prove that two angles are equal, identifying them as corresponding angles can be a quick and effective method.
Here's a step-by-step approach to using corresponding angles in proofs:
- Identify the parallel lines and transversal in your figure.
- Use the F-angle relationship to locate corresponding angles.
- State that these angles are equal because they are corresponding angles.
- Use this equality to support your proof or solve for unknown angles.
Remember, practice makes perfect! Try drawing various configurations of parallel lines and transversals, then challenge yourself to identify the corresponding angles. The more you work with these concepts, the more intuitive they'll become.
In conclusion, understanding corresponding angles and the F-angle relationship is like having a superpower in geometry. It allows you to quickly identify equal angles and simplify complex proofs. So next time you're faced with a geometric puzzle, just remember to look for that hidden "F" it might just be the key to unlocking the solution!
Alternate Interior and Exterior Angles
Alternate interior angles and alternate exterior angles are important concepts in geometry that help us understand the relationships between angles formed when a transversal line intersects two parallel lines. These angle pairs play a crucial role in solving various geometric problems and proofs.
Alternate interior angles are pairs of angles that lie on opposite sides of the transversal and inside the parallel lines. To identify these angles, imagine a "Z" shape formed by the transversal and the two parallel lines. The angles at the middle points of this "Z" are the alternate interior angles. These angles are always equal in measure when the lines are parallel.
Alternate exterior angles, on the other hand, are pairs of angles that lie on opposite sides of the transversal and outside the parallel lines. To locate these angles, picture an inverted "Z" shape. The angles at the outer points of this inverted "Z" are the alternate exterior angles. Like alternate interior angles, alternate exterior angles are also equal when the lines are parallel.
The Z-pattern is a helpful visual tool for identifying both alternate interior and exterior angles. For alternate interior angles, the Z is formed within the parallel lines, while for alternate exterior angles, the Z extends outside the parallel lines. This pattern makes it easier for students to recognize and remember these angle relationships.
The equality of alternate interior and exterior angles is a fundamental property of parallel lines cut by a transversal. This relationship exists because when two parallel lines are intersected by a transversal, corresponding angles are congruent. Alternate angles are essentially corresponding angles on opposite sides of the transversal, which is why they are equal.
To illustrate these concepts, consider two parallel horizontal lines intersected by a diagonal transversal. The angles formed inside the parallel lines, on opposite sides of the transversal, are alternate interior angles. If we measure these angles, we'll find they are equal. Similarly, the angles formed outside the parallel lines, on opposite sides of the transversal, are alternate exterior angles, and they too will have equal measures.
Understanding these angle relationships is crucial for solving more complex geometric problems. For example, when proving that two lines are parallel, showing that alternate interior or exterior angles are equal can be a key step. These concepts also form the basis for understanding other angle relationships, such as same-side interior angles.
In practical applications, alternate angles are used in various fields, including architecture, engineering, and navigation. Architects might use these principles when designing parallel structures or aligning building elements. Engineers apply these concepts in structural design and when working with parallel systems. In navigation, understanding these angle relationships can be helpful in plotting courses and determining directions.
To reinforce understanding, students can practice identifying alternate interior and exterior angles in various diagrams. They can also work on problems that involve calculating unknown angles using the properties of these angle pairs. Interactive geometry software can be a valuable tool for visualizing these relationships, allowing students to manipulate lines and angles to see how the relationships hold true.
In conclusion, alternate interior and exterior angles are fundamental concepts in geometry that provide insight into the relationships between angles formed by parallel lines and transversals. The Z-pattern serves as a useful mnemonic device for identifying these angles, while their equality is a key property that underlies many geometric proofs and problem-solving strategies. By mastering these concepts, students build a strong foundation for more advanced geometric studies and real-world applications.
Co-Interior Angles and Supplementary Relationships
Co-interior angles, also known as interior angles on the same side of the transversal, play a crucial role in geometry and parallel line relationships. These angles are formed when a transversal line intersects two other lines, creating a set of angles with unique properties. Understanding co-interior angles is essential for solving various geometric problems and exploring the fundamental principles of parallel lines.
By definition, co-interior angles are located on the same side of the transversal and between the two lines it intersects. What makes these angles particularly interesting is their supplementary relationship. In geometry, supplementary angles are two angles that add up to 180 degrees. This property holds true for co-interior angles when the two lines intersected by the transversal are parallel.
The reason co-interior angles are supplementary and always sum to 180 degrees lies in the properties of parallel lines. When a transversal crosses parallel lines, it creates corresponding angles, alternate interior angles, and co-interior angles. The supplementary nature of co-interior angles is a direct result of the parallel relationship between the two lines. This consistent 180-degree sum provides a powerful tool for solving geometric problems and proving theorems related to parallel lines.
To illustrate the concept, consider a pair of parallel lines intersected by a transversal. The co-interior angles formed on one side of the transversal will always add up to 180 degrees. For example, if one co-interior angle measures 65 degrees, we can immediately deduce that its supplementary co-interior angle must measure 115 degrees (180 - 65 = 115). This relationship holds true regardless of the specific measurements of the angles, as long as the lines remain parallel.
The supplementary property of co-interior angles is invaluable in problem-solving scenarios. For instance, when given the measure of one co-interior angle, we can easily calculate the measure of the other by subtracting the known angle from 180 degrees. This principle can be applied to more complex problems involving multiple angles and parallel lines, allowing geometers to deduce unknown angle measures and prove geometric relationships.
In addition to solving for unknown angles, the co-interior angle relationship can be used to prove that two lines are parallel. If we can demonstrate that a pair of angles on the same side of a transversal are supplementary, we can conclude that the lines intersected by the transversal must be parallel. This proof technique is frequently employed in geometric constructions and theoretical proofs.
It's worth noting that while co-interior angles focus on the interior region between two lines, there's a related concept known as exterior angles on the same side of the transversal. These exterior angles are formed outside the two lines intersected by the transversal. Interestingly, when the lines are parallel, these exterior angles also exhibit a supplementary relationship, mirroring the behavior of their interior counterparts.
The study of co-interior angles extends beyond basic geometry and finds applications in various fields. Architects and engineers utilize these principles when designing structures and ensuring proper alignment. In navigation and surveying, understanding co-interior angles helps in calculating distances and determining precise locations. Even in computer graphics and game design, these geometric relationships play a role in creating accurate and visually appealing environments.
Mastering the concept of co-interior angles and their supplementary nature provides a solid foundation for more advanced geometric studies. As students progress in their mathematical education, they'll find that this fundamental principle serves as a stepping stone to more complex theorems and proofs involving parallel lines, triangles, and other geometric shapes. The ability to recognize and apply the properties of co-interior angles is a valuable skill that enhances overall geometric reasoning and problem-solving capabilities.
Applying Angle Relationships in Problem Solving
Mastering angle relationships is crucial for success in geometry problem solving. To effectively apply these relationships, start by familiarizing yourself with the fundamental concepts such as complementary, supplementary, vertical, and corresponding angles. When approaching a geometry problem, carefully analyze the given information and diagram to identify potential angle relationships.
One key strategy is to look for parallel lines cut by a transversal, which often creates multiple angle relationships. Recognize that corresponding angles are congruent, alternate interior angles are congruent, and same-side interior angles are supplementary. When dealing with triangles, remember that the sum of interior angles in triangles is always 180 degrees, and exterior angles are supplementary to their adjacent interior angles.
Visualization is a powerful tool in geometry. Practice mentally rotating figures and tracing angles to spot hidden relationships. For complex diagrams, consider breaking them down into simpler shapes or extending lines to create additional angles that may reveal useful information. Don't hesitate to draw auxiliary lines to create new relationships that can help solve the problem.
Develop the habit of marking congruent angles and equal measures directly on the diagram. This visual aid can help you quickly identify patterns and relationships as you work through the problem. When dealing with polygons, remember that the exterior angles of polygons is always 360 degrees, regardless of the number of sides.
Efficiency in problem solving comes with practice. Work through a variety of problems to build your intuition for recognizing angle relationships quickly. Start with simpler problems and gradually increase complexity. As you solve each problem, reflect on the relationships you used and consider alternative approaches. This reflection will help reinforce your understanding and improve your problem-solving skills.
When stuck, try working backwards from the desired conclusion. This approach can often reveal the necessary steps and angle relationships needed to solve the problem. Additionally, don't forget to use solving angle problems with algebra. Many angle problems require setting up equations based on angle relationships and solving for unknown values.
Remember that angle relationships often work in combination. A single problem may require the application of multiple relationships to reach the solution. Develop a systematic approach to analyzing problems, considering each angle and its potential relationships to others in the figure. With consistent practice and a strategic approach, you'll become proficient in applying angle relationships to solve even the most challenging geometry problems.
Conclusion and Further Practice
In this lesson, we've explored essential angle relationships in geometry, including complementary, supplementary, vertical, and corresponding angles. Understanding these relationships is crucial for advancing in geometry and developing strong problem-solving skills. We've learned how to identify and calculate angles, which form the foundation for more complex geometric concepts. To reinforce your understanding, practice identifying these relationships in various problems and real-world scenarios. Try sketching different angle configurations and challenge yourself to recognize the relationships present. Remember, mastering these concepts will greatly benefit you in future geometry topics and mathematical reasoning. For additional practice, explore online geometry resources, work through textbook exercises, or join study groups to discuss and solve angle-related problems together. By consistently engaging with these concepts, you'll strengthen your geometry skills and prepare for more advanced mathematical challenges. Keep exploring and enjoy your journey through the fascinating world of geometry!
Understanding angle relationships is not only fundamental for geometry but also for trigonometry. When you calculate angles using trigonometric ratios, you apply these basic principles. This interconnectedness of mathematical concepts highlights the importance of a strong foundation in angle relationships. Keep practicing and exploring these ideas to excel in both geometry and trigonometry.
Example:
Below is a regular rectangular prism. Find.
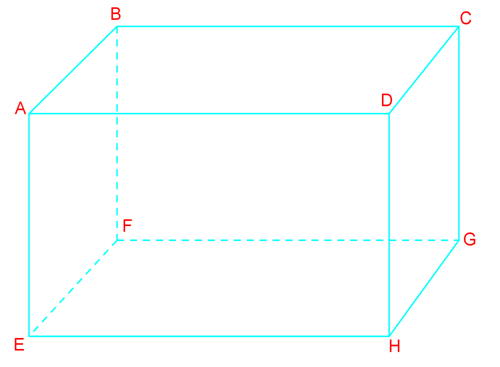
Line(s) that are perpendicular to .
Step 1: Understanding the Problem
To solve this problem, we need to identify the lines that are perpendicular to the line segment in a rectangular prism. A rectangular prism is a three-dimensional figure with six faces, all of which are rectangles. Each corner (or vertex) of the prism forms a 90-degree angle with its adjacent edges.
Step 2: Identifying the Line Segment
First, locate the line segment on the rectangular prism. In the given diagram, is one of the edges of the prism. For clarity, you can draw or highlight this line segment in a different color, such as yellow, to make it stand out.
Step 3: Criteria for Perpendicularity
For a line to be perpendicular to , it must meet the following criteria:
- It must be in the same plane as .
- It must intersect at a 90-degree angle.
Step 4: Identifying Perpendicular Lines
Next, identify the lines that meet the criteria for perpendicularity. In a rectangular prism, each edge is perpendicular to the edges that it intersects at a vertex. Therefore, we need to find the edges that intersect at a 90-degree angle.
Step 5: Listing Perpendicular Lines
From the diagram, we can see that the following lines are perpendicular to :
- : This line is perpendicular to as it intersects at vertex A.
- : This line is perpendicular to as it intersects at vertex B.
- : This line is perpendicular to as it intersects at vertex A.
- : This line is perpendicular to as it intersects at vertex B.
Step 6: Verifying Perpendicularity
To ensure that these lines are indeed perpendicular to , verify that each of these lines forms a 90-degree angle with and lies in the same plane. In a rectangular prism, all edges that meet at a vertex are perpendicular to each other, so this condition is satisfied.
Step 7: Conclusion
In conclusion, the lines that are perpendicular to in the given rectangular prism are , , , and . These lines meet the criteria of being in the same plane and intersecting at a 90-degree angle.
FAQs
Q1: What are parallel lines and how do they relate to transversals?
A1: Parallel lines are lines in the same plane that never intersect, no matter how far they extend. A transversal is a line that intersects two or more other lines at distinct points. When a transversal crosses parallel lines, it creates specific angle relationships, including corresponding angles, alternate interior angles, and alternate exterior angles, which are crucial for geometric proofs and problem-solving.
Q2: How can I identify corresponding angles using the F-angle relationship?
A2: The F-angle relationship is a visual method to identify corresponding angles. Imagine drawing an "F" shape using the parallel lines and transversal. The angles at the "tips" of the F are corresponding angles. This works regardless of the orientation of the lines. Corresponding angles are always equal when the lines are parallel, making this relationship useful in geometric proofs.
Q3: What are co-interior angles and why are they important?
A3: Co-interior angles, also known as same-side interior angles, are angles on the same side of the transversal and between the two lines it intersects. When the lines are parallel, co-interior angles are supplementary, meaning they add up to 180 degrees. This property is crucial for solving geometric problems and proving theorems related to parallel lines.
Q4: How can I apply angle relationships in problem-solving?
A4: To apply angle relationships in problem-solving, start by identifying parallel lines and transversals in the given diagram. Look for corresponding, alternate interior, and co-interior angles. Mark congruent angles and equal measures on the diagram. Use the properties of these angles (e.g., corresponding angles are equal, co-interior angles are supplementary) to set up equations and solve for unknown angles. Practice with various problems to build intuition and efficiency in recognizing these relationships.
Q5: How do angle relationships in geometry connect to other areas of mathematics?
A5: Angle relationships in geometry form the foundation for many other mathematical concepts. They are essential in trigonometry, where understanding angles is crucial for working with trigonometric functions. In calculus, angle relationships are used in analyzing curves and surfaces. In physics and engineering, these concepts are applied to understand forces, motion, and structural design. Mastering angle relationships in geometry provides a strong basis for advanced mathematical and scientific studies.
Prerequisite Topics for Understanding Pairs of Lines and Angles
When delving into the study of pairs of lines and angles, it's crucial to have a solid foundation in several key areas of geometry and algebra. Understanding these prerequisite topics will significantly enhance your ability to grasp the concepts and solve problems related to pairs of lines and angles.
One of the most fundamental prerequisites is parallel lines and transversals. This topic is essential because it introduces the concept of how lines interact and the various angles formed when a transversal crosses parallel lines. Mastering this concept will provide you with the necessary tools to analyze more complex line and angle relationships.
Another important area to focus on is the applications of linear equations. This algebraic foundation is crucial for understanding the mathematical representations of lines and their slopes. Being comfortable with linear equations will help you describe and analyze pairs of lines analytically, complementing your geometric understanding.
Familiarity with coordinate plane graphing is also beneficial. While this topic may seem more related to circles, it provides a valuable framework for visualizing and working with lines in a two-dimensional space. This skill will be particularly useful when you need to graph pairs of lines or determine their intersections.
A solid understanding of polygons is also relevant to the study of pairs of lines and angles. This topic introduces concepts such as alternate exterior angles, which are frequently encountered when working with intersecting lines. The principles learned in polygon geometry often apply to more general line and angle relationships.
Lastly, while it may not seem immediately obvious, knowledge of angle relationships in polygons can be surprisingly helpful. This trigonometric foundation provides a deeper understanding of how angles relate to each other, which is fundamental when analyzing pairs of lines and the angles they form.
By mastering these prerequisite topics, you'll build a strong foundation for understanding pairs of lines and angles. Each of these areas contributes unique insights and tools that will enhance your problem-solving abilities and deepen your comprehension of geometric relationships. Remember, geometry is an interconnected field, and a thorough grasp of these basics will serve you well as you progress to more advanced concepts.

