Inverse Functions: Unraveling Mathematical Relationships Dive into the world of inverse functions! Discover how to graph, analyze, and apply these powerful mathematical tools. Perfect for students looking to enhance their algebra and pre-calculus skills.
- Graph an inverse
Given the graph of y=f(x) as shown,
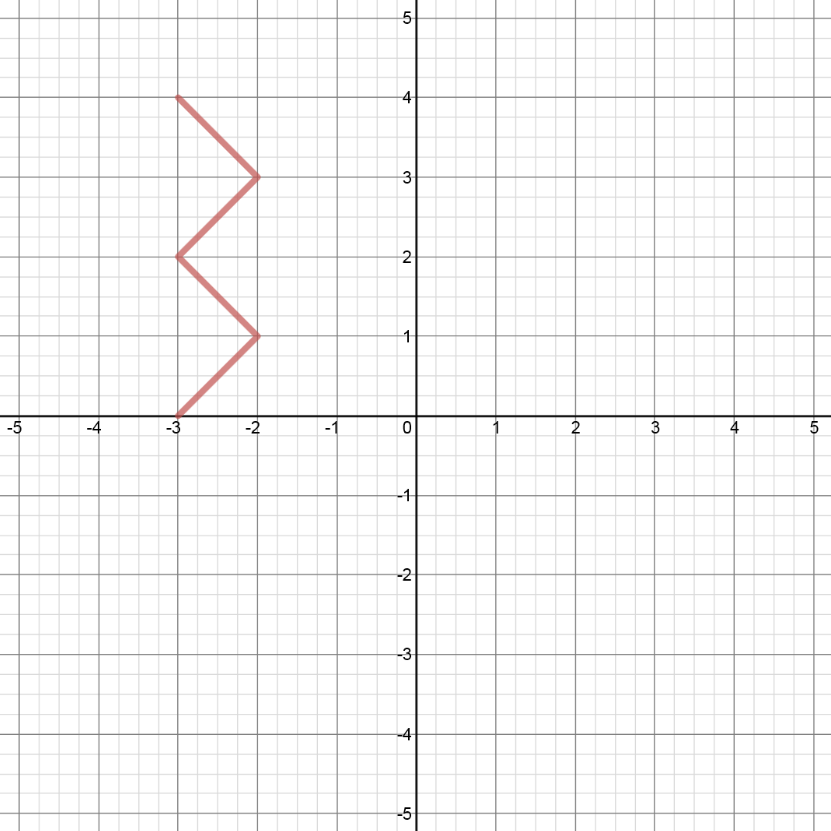
- Sketch the graph of the inverse y=f−1(x)
in 2 ways:
i) by reflecting f(x) in the line y=x
ii) by switching the x and y coordinates for each point on f(x) - Is f(x) a function?
Is f−1(x) a function?
- Sketch the graph of the inverse y=f−1(x)
in 2 ways:
- Inverse of a Quadratic Function
Consider the quadratic function: f(x)=(x+4)2+2 - Determine the equation of the inverse.
Algebraically determine the equation of the inverse f−1(x), given:
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Introduction to Inverse Functions
Inverse functions are a fundamental concept in mathematics that play a crucial role in various applications. Our introduction video serves as an excellent starting point for understanding inverse functions. An inverse function essentially "undoes" what the original function does, reversing its operations. This means that if you apply a function and then its inverse to a value, you'll end up back where you started. One key characteristic of inverse functions is that they swap the x and y coordinates of every point on the original function's graph. This property is visually represented by reflecting the graph over the line y=x. Understanding inverse functions is vital for solving equations, modeling real-world scenarios, and advancing in higher mathematics. As you delve deeper into this concept, you'll discover its applications in fields such as physics, engineering, and economics. The introduction video will provide you with a solid foundation to explore these fascinating mathematical relationships further.
Inverse of a Quadratic Function
Consider the quadratic function: f(x)=(x+4)2+2
Graph the function f(x) and
state the domain and range.
Step 1: Identify the Form of the Quadratic Function
The given quadratic function is f(x)=(x+4)2+2. This function is in vertex form, which is generally written as f(x)=a(x−h)2+k, where (h,k) is the vertex of the parabola. In this case, the vertex form allows us to easily identify the vertex of the quadratic function.
Step 2: Determine the Vertex
From the function f(x)=(x+4)2+2, we can see that the vertex (h,k) is (−4,2). This is because the function can be rewritten as f(x)=(x−(−4))2+2, making it clear that h=−4 and k=2.
Step 3: Determine the Direction of the Parabola
Since the coefficient of the squared term (x+4)2 is positive (which is 1 in this case), the parabola opens upwards. This means that as x moves away from the vertex, the value of f(x) increases.
Step 4: Create a Table of Values
To graph the function accurately, it is helpful to create a table of values. We will choose values of x around the vertex −4 and calculate the corresponding y values.
- For x=−6: f(−6)=(−6+4)2+2=(−2)2+2=4+2=6
- For x=−5: f(−5)=(−5+4)2+2=(−1)2+2=1+2=3
- For x=−4: f(−4)=(−4+4)2+2=02+2=2
- For x=−3: f(−3)=(−3+4)2+2=12+2=1+2=3
- For x=−2: f(−2)=(−2+4)2+2=22+2=4+2=6
Step 5: Plot the Points and Draw the Parabola
Using the points from the table of values, plot the points (−6,6), (−5,3), (−4,2), (−3,3), and (−2,6) on a coordinate plane. Connect these points with a smooth curve to form the parabola. The graph should be symmetric about the vertical line x=−4.
Step 6: State the Domain
The domain of a quadratic function is all real numbers because the function is defined for every value of x. Therefore, the domain of f(x)=(x+4)2+2 is:
Domain: x∈R
Step 7: State the Range
The range of the function is determined by the vertex and the direction in which the parabola opens. Since the parabola opens upwards and the vertex is at (−4,2), the minimum value of f(x) is 2. Therefore, the range of f(x)=(x+4)2+2 is:
Range: y≥2
Q1: What is an inverse function?
A1: An inverse function "undoes" what the original function does. It reverses the operation of the original function, essentially swapping the input and output. If f(x) is a function, its inverse is denoted as f^(-1)(x). For example, if f(x) = 2x + 3, then f^(-1)(x) = (x - 3) / 2.
Q2: How can I tell if a function has an inverse?
A2: A function has an inverse if it's both one-to-one (injective) and onto (surjective). Graphically, you can use the horizontal line test: if any horizontal line intersects the graph of the function more than once, it doesn't have an inverse. Algebraically, ensure that each y-value corresponds to only one x-value.
Q3: What's the relationship between a function's graph and its inverse's graph?
A3: The graph of an inverse function is a reflection of the original function's graph over the line y = x. This means if you draw a line from any point on the original function perpendicular to y = x, it will intersect the inverse function at a point that's equidistant from y = x.
Q4: How do I find the inverse of a function algebraically?
A4: To find the inverse: 1) Replace f(x) with y, 2) Swap x and y in the equation, 3) Solve the new equation for y, 4) Replace y with f^(-1)(x). For example, if f(x) = 2x + 3, swap x and y to get x = 2y + 3, then solve for y to get y = (x - 3) / 2, so f^(-1)(x) = (x - 3) / 2.
Q5: What are some real-world applications of inverse functions?
A5: Inverse functions have numerous practical applications: 1) Temperature conversion between Celsius and Fahrenheit, 2) Calculating compound interest and determining principal amounts in finance, 3) Encryption and decryption in cryptography, 4) Solving motion problems in physics, 5) 3D modeling and animation in computer graphics.
Mastering inverse functions requires a solid foundation in several key mathematical concepts. One of the most fundamental is function notation, which provides the language to express and manipulate functions effectively. Understanding how to read and write functions is crucial when working with their inverses.
Equally important is grasping the domain and range of a function. These concepts are essential because the domain of an inverse function is the range of the original function, and vice versa. This relationship is key to determining whether a function has an inverse and defining its properties.
The horizontal line test is a critical tool in determining whether a function has an inverse. This test, which relates to special cases of linear equations, helps students visualize and understand the one-to-one nature required for a function to have an inverse.
While not directly related, understanding solving linear systems using 2x2 inverse matrices can provide valuable insights into the broader concept of inverse operations in mathematics. This knowledge can enhance overall mathematical reasoning when dealing with inverse functions.
Concepts like continuous growth and decay often involve exponential functions, which have important inverse relationships with logarithmic functions. This connection highlights the practical applications of inverse functions in real-world scenarios.
For those advancing to calculus, understanding the derivative of inverse trigonometric functions becomes crucial. This topic bridges the gap between algebra and calculus, showcasing how inverse functions play a role in more advanced mathematical concepts.
The applications of polynomial functions provide context for why inverse functions are important, as many real-world problems involve finding reverse relationships between variables.
While seemingly unrelated, topics like conversions between metric and imperial systems can help students appreciate the practical use of inverse relationships in everyday life.
Financial concepts such as compound interest often involve exponential growth, which relates to inverse functions when solving for time or interest rates.
Lastly, understanding kinematic equations in one dimension can provide physical context for inverse functions, as many physics problems involve finding inverse relationships between variables like position, velocity, and time.
By mastering these prerequisite topics, students will be well-prepared to tackle the complexities of inverse functions, understanding not just how to manipulate them mathematically, but also how they relate to various real-world applications and more advanced mathematical concepts.



