Sign In
Try for Free
 flag-uk

Mastering the Disc Method for Volumes of Revolution
Unlock the power of the disc method to calculate volumes of solids of revolution. Perfect your calculus skills with our comprehensive guide, from basic concepts to advanced applications.

  1. Intros0/1 watched
  2. Examples0/6 watched
  3. Practice0/3 practiced
  1. 0/1
  2. 0/6
  3. 0/3
Now Playing:Volumes of solids of revolution disc method– Example 0
Intros
0/1 watched
  1. How to find the volume of solids of revolution using the Disc method.
Examples
0/6 watched
  1. The region bounded by the graphs of y=exy=e^x, y=0y=0,x=0x=0, and x=1x=1 is revolved about the x-axis. Find the volume of the resulting solid.
    Practice
    0/3
    Volumes Of Solids Of Revolution Disc Method 2
    Volumes of solids of revolution - Disc method
    Jump to:NotesConceptFAQsPrerequisites
    Notes
    In this lesson, we learn that rotating the function around the x-axis will give us a solid. This is known as the disc method. You notice that the cross sections of the solid are always circles. This is important because we know the area of the circle, and integrating this will give us the volume. We also learn that the radius of the circle is simply the function itself. In more advanced questions, we see that we can use the region between two curves and rotate it around the x-axis. However, the cross section is the region between the two circles. Hence, the radius will be the outer radius minus the inner radius. In this section, you will also deal with questions which involve rotating functions around the y-axis.
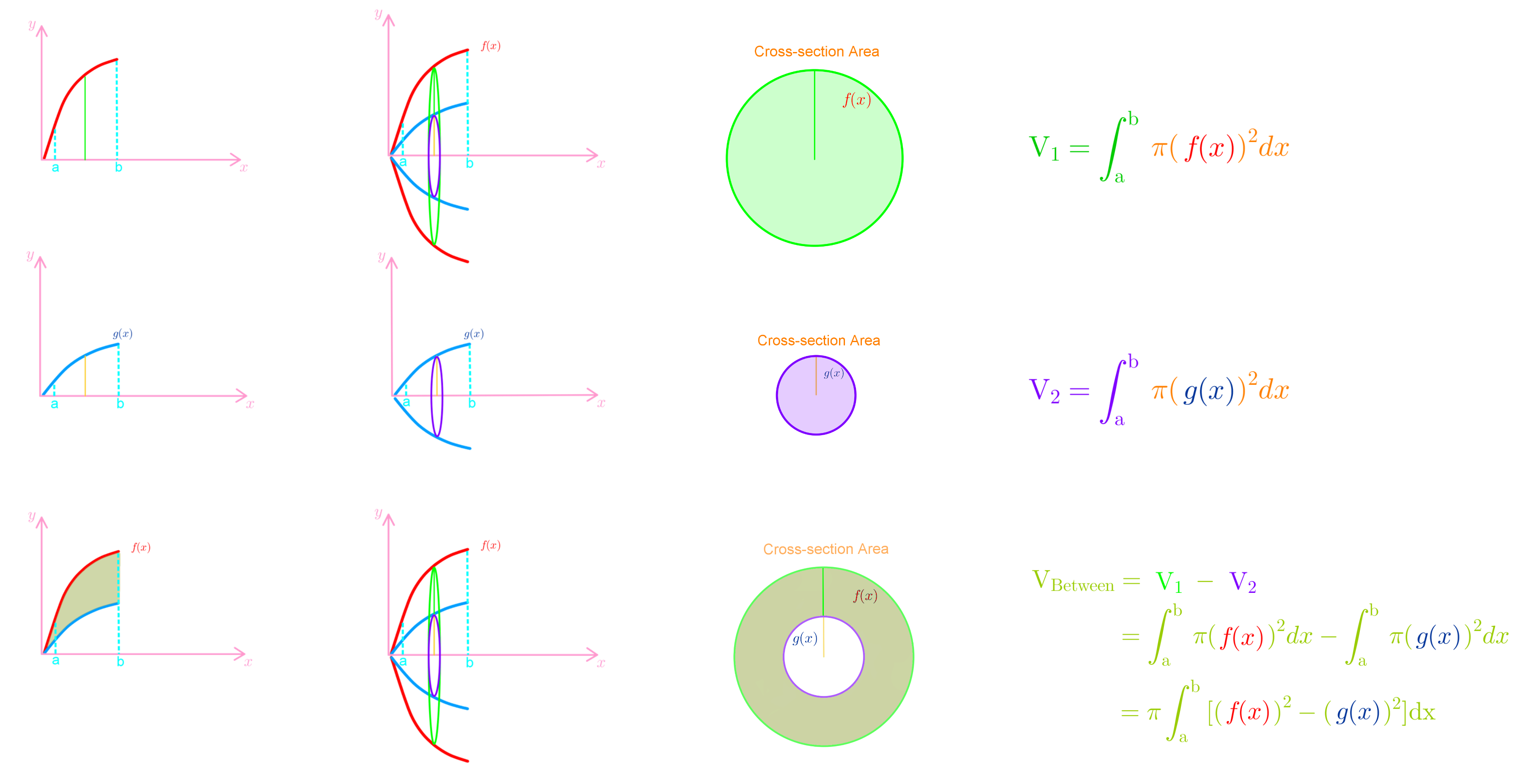
    using Disc method to find volumes of solids of revolution
    Concept

    Introduction to Volumes of Solids of Revolution: The Disc Method

    The disc method is a powerful technique for calculating volumes of solids of revolution in calculus. This approach is particularly useful when dealing with objects formed by rotating a region around an axis. Our introduction video provides a comprehensive overview of this concept, serving as an essential starting point for students. The video demonstrates how to visualize and apply the disc method, making it easier to grasp this sometimes challenging topic. It's important to note that the disc method is actually a special case of finding volumes with known cross-sections. By understanding this connection, students can develop a broader perspective on volume calculation techniques. The disc method involves slicing the solid into thin circular discs, then summing up their volumes. This process is typically executed using integration, allowing for precise calculations of three-dimensional shapes. Mastering the disc method opens doors to solving a wide range of real-world problems in engineering, physics, and other scientific fields.

    Understanding the volumes of solids of revolution is crucial for students aiming to excel in calculus. The disc method, as a special case, provides a solid foundation for more advanced topics. By mastering this technique, students can confidently tackle problems involving precise calculations of three-dimensional shapes, which are common in various scientific and engineering applications.

    FAQs

    Here are some frequently asked questions about the disc method in calculus:

    What is the disk method?

    The disk method is a technique used in calculus to calculate the volume of a solid formed by rotating a region bounded by a function and the x-axis around the x-axis. It involves integrating the areas of circular disks that make up the solid.

    What is the difference between disc method and washer method?

    The disc method is used when rotating a single function around an axis, while the washer method is used when rotating the region between two functions. The washer method subtracts the inner function's area from the outer function's area to find the volume of the resulting hollow solid.

    What is the disk method in AP calculus?

    In AP Calculus, the disk method is taught as a way to find volumes of solids of revolution. Students learn to set up and evaluate integrals of the form V = π (f(x))² dx, where f(x) is the function being rotated around the x-axis.

    When to use shell or disk method?

    Use the disk method when rotating around the x-axis and the function is easily expressed as y = f(x). Use the shell method when rotating around the y-axis or when the function is more easily expressed as x = g(y). The shell method is often more convenient for rotations around vertical lines.

    How do you determine the limits of integration for the disk method?

    The limits of integration for the disk method are determined by the interval over which the function is being rotated. These are typically the x-values where the rotation starts and ends. For example, if rotating y = f(x) from x = a to x = b, the integral would be set up as V = π (a to b) (f(x))² dx.

    Prerequisites

    Understanding the volumes of solids of revolution using the disc method is a crucial concept in calculus, but it requires a strong foundation in several prerequisite topics. One of the fundamental skills needed is the ability to recognize the relationship between two variables, as this forms the basis for understanding how a function's graph can be rotated to create a three-dimensional solid.

    Before diving into the disc method, it's essential to have a solid grasp of volumes of solids with known cross-sections. This concept serves as a stepping stone to understanding how the disc method works by slicing the solid into thin circular discs. Additionally, familiarity with the surface area of 3D shapes provides valuable insight into how these solids are constructed and measured.

    A strong algebraic foundation is crucial, including the ability to solve polynomials with unknown variables. This skill is particularly useful when dealing with complex functions that generate the solids of revolution. Understanding vertical lines and horizontal lines of linear equations is also important, as these concepts help in visualizing the boundaries of the solid being rotated.

    The disc method is closely related to finding areas between curves, as both involve integration techniques. Proficiency in conversions involving squares and cubic measurements is essential when calculating volumes, as you'll often need to convert between different units of measurement.

    Practical application of these concepts can be seen in word problems relating to volumes of prisms and cylinders. These problems provide a foundation for understanding how the disc method extends to more complex shapes. It's also worth noting that the disc method is closely related to the shell method for calculating volumes of solids of revolution, and understanding both methods can provide a more comprehensive grasp of the topic.

    By mastering these prerequisite topics, students will be better equipped to tackle the complexities of the disc method for calculating volumes of solids of revolution. Each concept builds upon the others, creating a robust framework for understanding this advanced calculus technique. Remember, a solid foundation in these prerequisites is key to success in more advanced mathematical concepts.