Probability of independent events
Topic Notes
Introduction to Probability of Independent Events
Understanding the probability of independent events is a fundamental concept in statistics and probability theory. Our introduction video serves as an excellent starting point for grasping this crucial topic. Independent events are occurrences where the outcome of one event does not affect the probability of another event happening. This concept is essential for accurately calculating probabilities in various real-world scenarios. The video explains how to identify independent events and apply the multiplication rule to determine their combined probability. By mastering this concept, students can tackle more complex probability problems and develop a strong foundation in statistical analysis. The importance of understanding independent events extends beyond academic settings, as it has practical applications in fields such as finance, science, and decision-making. This introduction sets the stage for exploring more advanced probability concepts and their real-world applications.
Understanding Independent Events
In the realm of probability, independent events play a crucial role in understanding how different occurrences relate to one another. Independent events are defined as two or more events where the outcome of one event does not affect the probability of the other event occurring. This concept is fundamental in probability theory and has wide-ranging applications in various fields, from statistics to everyday decision-making.
To better grasp the concept of independent events, it's essential to contrast them with dependent events. In dependent events, the outcome of one event does influence the probability of another event. For example, drawing cards from a deck without replacement creates dependent events, as each draw changes the composition of the remaining cards, affecting subsequent probabilities.
A classic example of independent events, as illustrated in the video, involves flipping a coin and rolling a die. These two actions perfectly demonstrate the principle of independence in probability. When you flip a coin, the outcome - whether it lands on heads or tails - has absolutely no bearing on the result of rolling a die. Similarly, the number that appears on the die after rolling it does not influence the outcome of any subsequent coin flip.
Let's break this down further. When you flip a fair coin, there's always a 50% chance of getting heads and a 50% chance of getting tails. This probability remains constant, regardless of how many times you flip the coin or what other events occur. Now, consider rolling a fair six-sided die. The probability of rolling any number from 1 to 6 is always 1/6, or approximately 16.67%. These probabilities remain unchanged whether you've just flipped a coin or not.
The key takeaway here is that the outcome of the coin flip does not affect the probability of the die roll, and vice versa. This lack of influence between events is the hallmark of independence in probability. You could flip the coin a hundred times, getting heads every single time, and it would not change the probability of rolling a specific number on the die.
Understanding independent events is crucial in many real-world scenarios. For instance, in weather forecasting, the chance of rain tomorrow is generally independent of whether it rained today (assuming no larger weather patterns are at play). In genetics, the inheritance of certain traits can be independent events. Even in everyday life, recognizing independent events can help in making more rational decisions and avoiding the gambler's fallacy - the mistaken belief that if something happens more frequently than normal during a given period, it will happen less frequently in the future, or vice versa.
To further illustrate the concept, consider this: if you were to flip a coin and roll a die simultaneously, the probability of getting heads on the coin and a 3 on the die would be the product of their individual probabilities. This multiplication rule for independent events states that P(A and B) = P(A) × P(B), where A and B are independent events. In this case, it would be 1/2 × 1/6 = 1/12, or about 8.33%.
In conclusion, independent events in probability are characterized by their mutual non-influence. The coin flip and die roll example serves as a perfect illustration of this concept, demonstrating how the outcome of one event has no impact on the probability of the other. Recognizing and understanding independent events is not just a mathematical exercise but a valuable skill that can enhance our understanding of chance and probability in various aspects of life and scientific inquiry.
Calculating Probability of Independent Events
Understanding how to calculate the probability of independent events occurring together is a fundamental concept in probability theory. This knowledge is crucial for various fields, including statistics, data science, and decision-making processes. In this section, we'll explore the method for calculating such probabilities, introduce the multiplication rule for independent events, and provide a step-by-step guide using practical examples.
The key to calculating the probability of independent events occurring together lies in the multiplication rule. This rule states that for two or more independent events, the probability of them all occurring is equal to the product of their individual probabilities. In mathematical terms, if A and B are independent events, then:
P(A and B) = P(A) × P(B)
Let's break down this concept using a common example: flipping a coin and rolling a die. These are classic independent events because the outcome of one does not affect the outcome of the other.
Example: What is the probability of getting heads on a coin flip AND rolling a 6 on a die?
Step 1: Identify the individual probabilities - Probability of getting heads on a coin flip: P(H) = 1/2 - Probability of rolling a 6 on a die: P(6) = 1/6
Step 2: Apply the multiplication rule P(H and 6) = P(H) × P(6) = 1/2 × 1/6 = 1/12
Therefore, the probability of getting heads on a coin flip AND rolling a 6 on a die is 1/12.
This example demonstrates how the multiplication rule simplifies the calculation of probabilities for independent events. The beauty of this rule is that it can be extended to any number of independent events. For instance, if we were to add a third independent event, like drawing an ace from a deck of cards, we would simply multiply its probability by our previous result.
Here's a step-by-step guide for solving probability problems involving independent events:
1. Identify the events and confirm they are independent. 2. Determine the individual probability of each event. 3. Multiply the individual probabilities together. 4. The result is the probability of all events occurring together.
It's important to note that this method only applies to independent events. Events are considered independent if the occurrence of one event does not affect the probability of the other event(s) occurring. In our coin flip and die roll example, the outcome of the coin flip has no impact on the outcome of the die roll, making them independent.
Let's consider another example to reinforce this concept:
Example: What is the probability of drawing a king from a standard deck of cards, replacing it, and then drawing a heart?
Step 1: Identify the individual probabilities - Probability of drawing a king: P(K) = 4/52 = 1/13 - Probability of drawing a heart: P(H) = 13/52 = 1/4
Step 2: Apply the multiplication rule P(K and H) = P(K) × P(H) = 1/13 × 1/4 = 1/52
The probability of drawing a king and then a heart (with replacement) is 1/52.
Understanding and applying the multiplication rule for independent events is crucial in various real-world scenarios. For instance, in quality control, you might need to calculate the probability of multiple independent components all functioning correctly. In weather forecasting, you might need to determine the likelihood of specific weather conditions occurring simultaneously in different locations.
As you become more comfortable with this concept, you'll find that it's a powerful tool for analyzing complex situations involving multiple independent factors. Remember, the key is to ensure that the events are truly independent before applying the multiplication rule.
In conclusion, calculating the probability of independent events occurring together is a straightforward process when you understand and apply the multiplication rule. By breaking down complex scenarios into individual probabilities and then multiplying them, you can solve a
Using Tree Diagrams for Independent Events
Tree diagrams are powerful visual tools for representing and analyzing independent events in probability. These diagrams provide a clear, structured approach to understanding complex probability scenarios, making them particularly useful for independent events. In this section, we'll explore how to create and use tree diagrams, their benefits for independent events, and walk through a detailed example using a coin flip and die roll scenario.
To create a tree diagram for independent events, start with a root node representing the initial state. From this node, draw branches for each possible outcome of the first event. At the end of each branch, create new nodes and repeat the process for subsequent events. This branching structure allows for a clear visualization of all possible combinations of outcomes.
Tree diagrams are especially valuable for independent events because they clearly illustrate the multiplicative nature of probabilities. Each branch represents a distinct path, and the probability of following that path is the product of the individual probabilities along it. This visual representation makes it easier to understand and calculate compound probabilities.
Let's consider a detailed example using a coin flip followed by a die roll. In this scenario, we'll flip a fair coin (with outcomes Heads or Tails) and then roll a fair six-sided die (with outcomes 1 through 6). To create the tree diagram:
1. Start with a root node representing the initial state.
2. Draw two branches from the root, one for Heads (H) and one for Tails (T), each with a probability of 1/2.
3. At the end of each of these branches, draw six new branches representing the possible outcomes of the die roll (1, 2, 3, 4, 5, 6), each with a probability of 1/6.
4. Label each branch with its respective probability.
The resulting tree diagram will have two main branches (H and T) from the root, each splitting into six sub-branches for the die roll outcomes. This structure clearly shows all 12 possible combinations of coin flip and die roll results.
To interpret the diagram and find probabilities:
1. For the probability of a specific path, multiply the probabilities along that path. For example, the probability of getting Heads and rolling a 3 is: 1/2 × 1/6 = 1/12.
2. For the probability of multiple outcomes, sum the probabilities of the relevant paths. For instance, the probability of getting Tails and an even number on the die is: (1/2 × 1/6) + (1/2 × 1/6) + (1/2 × 1/6) = 1/4.
3. To find the total probability of an event occurring in either the first or second stage, add the probabilities of all relevant paths. For example, the probability of either getting Heads or rolling a 6 is: 1/2 + (1/2 × 1/6) = 7/12.
Tree diagrams excel at visualizing independent events because they clearly show how each event's outcome doesn't affect subsequent events. In our example, the probability of each die roll outcome remains 1/6 regardless of the coin flip result, illustrating the independence of these events.
By using tree diagrams, complex probability problems become more manageable. They provide a systematic way to enumerate all possible outcomes, calculate individual and compound probabilities, and identify patterns in probability distributions. This visual approach not only aids in solving probability problems but also enhances understanding of the underlying concepts of independent events and probability multiplication.
In conclusion, tree diagrams are invaluable tools for visualizing and analyzing independent events in probability. They offer a clear, structured representation of all possible outcomes, facilitate easy calculation of compound probabilities, and provide insights into the nature of independent events. By mastering the creation and interpretation of tree diagrams, you'll be well-equipped to tackle a wide range of probability problems involving independent events.
Comparing Independent and Dependent Events
Understanding the distinction between independent and dependent events is crucial in probability theory. These concepts play a significant role in various fields, from statistics to everyday decision-making. Let's explore the key differences between independent and dependent events, using the marble example to illustrate dependent events and highlighting how probability calculations differ between the two.
Independent events are occurrences where the outcome of one event does not affect the probability of another event happening. For instance, when flipping a coin twice, the result of the first flip doesn't influence the outcome of the second flip. Each flip maintains a constant probability of 1/2 for heads or tails, regardless of previous results.
Conversely, dependent events are interconnected, where the occurrence of one event impacts the probability of subsequent events. The marble example from the video perfectly demonstrates this concept. Imagine a bag containing five marbles: three red and two blue. When drawing marbles without replacement, each draw affects the composition of the remaining marbles, thus altering the probabilities for subsequent draws.
Let's examine this marble scenario more closely. On the first draw, the probability of selecting a red marble is 3/5. If a red marble is indeed drawn and not replaced, the bag now contains two red marbles and two blue marbles. For the second draw, the probability of selecting another red marble has changed to 2/4 or 1/2. This shift in probability exemplifies the nature of dependent events.
The key difference in probability calculations between independent and dependent events lies in how we approach subsequent probabilities. For independent events, we simply multiply the individual probabilities of each event occurring. If we were drawing marbles with replacement (making the events independent), the probability of drawing two red marbles would be (3/5) × (3/5) = 9/25.
However, for dependent events, we must consider how each event changes the probability landscape for subsequent events. In our marble example without replacement, the probability of drawing two red marbles becomes (3/5) × (2/4) = 3/10. This calculation reflects the changing composition of the marble bag after each draw.
One of the most significant distinctions between independent and dependent events is the behavior of the sample space. The sample space represents all possible outcomes of an experiment. For independent events, the sample space remains constant throughout the experiment. In the coin flip example, the sample space always consists of two outcomes (heads or tails) for each flip, regardless of previous results.
In contrast, the sample space for dependent events changes with each occurrence. Returning to our marble example, the initial sample space consists of five marbles. After the first draw, the sample space reduces to four marbles, with a different composition depending on which color was drawn first. This dynamic nature of the sample space is a hallmark of dependent events and directly impacts probability calculations.
Understanding these differences is crucial for accurately assessing probabilities in various scenarios. In real-world applications, recognizing whether events are independent or dependent can significantly affect decision-making processes, risk assessments, and statistical analyses. For instance, in genetics, the inheritance of certain traits can be dependent events, while in weather forecasting, some meteorological phenomena might be treated as independent events.
To summarize, independent events maintain constant probabilities and a fixed sample space, allowing for straightforward multiplication of individual event probabilities. Dependent events, however, require a more nuanced approach, considering how each event alters the probability landscape and sample space for subsequent events. The marble example vividly illustrates this concept, showing how the act of drawing a marble without replacement changes the probabilities for future draws. By grasping these fundamental differences, one can more accurately navigate the complex world of probability and make more informed decisions based on statistical reasoning.
Practice Problems and Applications
Let's dive into some practice problems involving independent events and explore their real-world applications. Remember, independent events are occurrences where the outcome of one event does not affect the probability of the other. Before we reveal the solutions, try solving these problems on your own to reinforce your understanding.
Problem 1: Coin Toss and Die Roll
You toss a fair coin and roll a fair six-sided die. What is the probability of getting heads on the coin and an even number on the die?
Problem 2: Weather Forecast
The weather forecast predicts a 70% chance of rain tomorrow and a 60% chance of rain the day after. Assuming these events are independent, what is the probability that it will rain on both days?
Problem 3: Product Defects
A factory produces two types of components, A and B. The probability of a defect in component A is 0.05, and the probability of a defect in component B is 0.03. If these defects occur independently, what is the probability that both components are defective?
Problem 4: Card Draw
You draw two cards from a standard 52-card deck with replacement. What is the probability of drawing two hearts?
Solutions:
Solution 1: Coin Toss and Die Roll
Step 1: Identify the probabilities
P(Heads) = 1/2
P(Even number on die) = 3/6 = 1/2
Step 2: Apply the multiplication rule for independent events
P(Heads and Even) = P(Heads) × P(Even) = 1/2 × 1/2 = 1/4
Solution 2: Weather Forecast
Step 1: Convert percentages to probabilities
P(Rain tomorrow) = 0.70
P(Rain day after) = 0.60
Step 2: Apply the multiplication rule
P(Rain both days) = 0.70 × 0.60 = 0.42 or 42%
Solution 3: Product Defects
Step 1: Identify the probabilities
P(Defect in A) = 0.05
P(Defect in B) = 0.03
Step 2: Apply the multiplication rule
P(Both defective) = 0.05 × 0.03 = 0.0015 or 0.15%
Solution 4: Card Draw
Step 1: Identify the probability of drawing a heart
P(Heart) = 13/52 = 1/4
Step 2: Apply the multiplication rule (with replacement)
P(Two hearts) = 1/4 × 1/4 = 1/16
These problems demonstrate the wide-ranging applications of independent event probability in various fields:
- Gaming and gambling (coin tosses, dice rolls, card games)
- Meteorology and climate science (weather predictions)
- Manufacturing and quality control (product defects)
- Finance and risk assessment (stock market movements)
- Healthcare (genetic inheritance, drug efficacy)
- Transportation (flight delays, traffic patterns)
To visualize these problems, consider using tree diagrams for probability. For example, in Problem 1, you can draw a tree with two main branches for the coin toss (H and T), and then six sub-branches for each die roll outcome. This visual representation helps in understanding the problem better.
Conclusion
Understanding the probability of independent events is crucial in statistics. As demonstrated in the introduction video, independent events occur when the outcome of one event does not affect the probability of another. The key to calculating their combined probability lies in multiplying individual probabilities. This concept forms the foundation for more complex probability scenarios. Mastering independent events opens doors to understanding dependent events and conditional probability. To solidify your grasp on this topic, it's essential to practice probability problems with various problems and scenarios. Explore additional resources on probability and statistics to broaden your knowledge. Remember, proficiency in probability calculations is valuable in many fields, from data science to finance. By continuing to study and apply these concepts, you'll develop a strong statistical intuition that will serve you well in both academic and professional settings. Keep practicing and exploring the fascinating world of probability!
Example:
Sam is hunting a treasure. He is equally likely to travel along any pathway. His trip ends at 1, 2, 3, 4, 5, or 6.
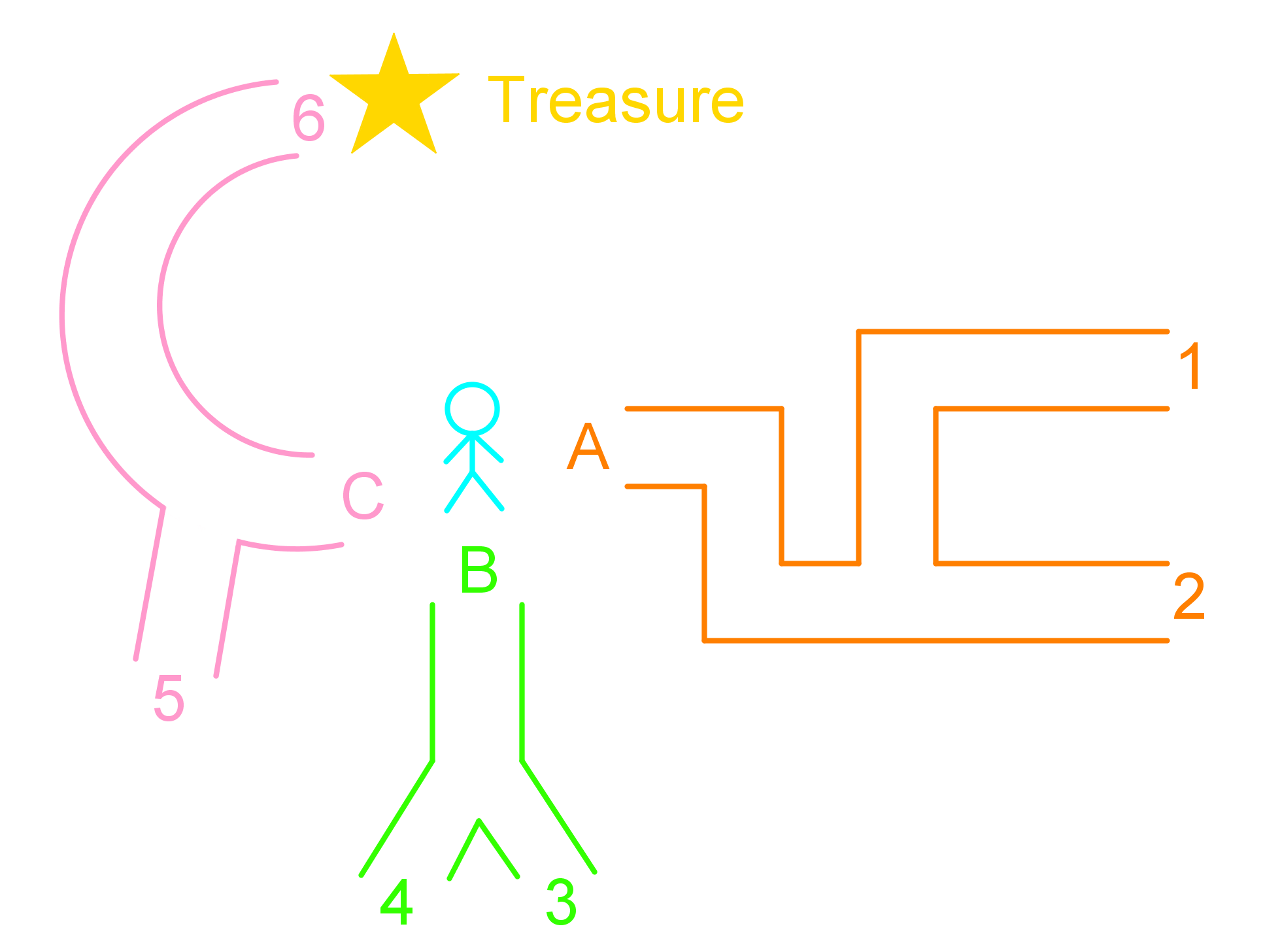
What is the probability that Sam finds the treasure?
Step 1: Understanding the Problem
First, we need to understand the problem. Sam is equally likely to travel along any of the pathways shown in the diagram. His trip can end at one of six possible locations: 1, 2, 3, 4, 5, or 6. We need to determine the probability that Sam finds the treasure, which is located at one of these endpoints.
Step 2: Identifying the Possible Outcomes
Next, we identify all possible outcomes. According to the problem, Sam's trip can end at any of the six locations: 1, 2, 3, 4, 5, or 6. These are our possible outcomes. Since Sam is equally likely to travel along any pathway, each of these outcomes has the same probability of occurring.
Step 3: Determining the Favorable Outcome
We need to determine the favorable outcome, which is the event where Sam finds the treasure. According to the diagram, the treasure is located at endpoint 6. Therefore, the favorable outcome is Sam ending his trip at location 6.
Step 4: Calculating the Probability
To calculate the probability of Sam finding the treasure, we use the formula for theoretical probability. Theoretical probability is calculated as the number of favorable outcomes divided by the total number of possible outcomes. In this case, there is 1 favorable outcome (ending at location 6) and 6 possible outcomes (ending at any of the six locations).
Step 5: Applying the Formula
Using the formula for theoretical probability, we get:
Probability (P) = Number of Favorable Outcomes / Total Number of Possible Outcomes
Substituting the values, we get:
P = 1 / 6
Step 6: Interpreting the Result
The probability that Sam finds the treasure is 1/6. This means that if Sam were to take this trip multiple times, he would find the treasure approximately one out of every six trips. Since the question does not specify that the answer needs to be in a different format, we can leave the probability as a fraction.
FAQs
-
What are independent events in probability?
Independent events are occurrences where the outcome of one event does not affect the probability of another event happening. For example, flipping a coin and rolling a die are independent events because the result of the coin flip doesn't influence the outcome of the die roll.
-
How do you calculate the probability of two independent events occurring together?
To calculate the probability of two independent events occurring together, you multiply their individual probabilities. This is known as the multiplication rule for independent events. For instance, if the probability of event A is P(A) and the probability of event B is P(B), then the probability of both A and B occurring is P(A) × P(B).
-
What's the difference between independent and dependent events?
Independent events do not affect each other's probabilities, while dependent events do. In independent events, the occurrence of one event doesn't change the probability of the other event. In dependent events, the probability of the second event changes based on the outcome of the first event.
-
Can you give an example of independent events in real life?
A common real-life example of independent events is weather in different cities. The chance of rain in New York doesn't typically affect the chance of rain in Los Angeles on the same day. Another example is drawing cards from a deck with replacement; each draw is independent if you replace the card after each selection.
-
How can tree diagrams help in understanding independent events?
Tree diagrams are visual tools that help represent all possible outcomes of a series of events. For independent events, tree diagrams clearly show how the probability of each branch remains constant, regardless of previous outcomes. They make it easier to visualize and calculate compound probabilities by multiplying probabilities along each path.
Prerequisite Topics for Understanding Probability of Independent Events
When delving into the world of probability, particularly the concept of independent events, it's crucial to have a solid foundation in certain prerequisite topics. These foundational concepts not only enhance your understanding but also provide the necessary tools to tackle more complex probability problems with confidence.
One of the key prerequisites is understanding the exponent product rule. This algebraic concept, which states that (a^x)(a^y) = a^(x+y), might seem unrelated at first glance. However, it plays a vital role in probability calculations, especially when dealing with the multiplication rule for probability. The exponent product rule helps simplify complex probability expressions, making it easier to compute probabilities of multiple independent events occurring together.
Another essential prerequisite is the ability to determine probabilities using tree diagrams and tables. This skill is particularly valuable when working with probability of independent events. Tree diagrams provide a visual representation of different possible outcomes, making it easier to identify and calculate probabilities of specific event combinations. They are especially useful for understanding how probabilities multiply when dealing with independent events.
Mastering these prerequisites will significantly enhance your ability to work with probabilities of independent events. The exponent product rule aids in simplifying calculations, while tree diagrams offer a clear visual method for organizing and computing probabilities. Together, these skills form a strong foundation for tackling more advanced probability concepts.
When studying probability of independent events, you'll find that the multiplication rule for probability is a central concept. This rule states that for independent events A and B, the probability of both occurring is the product of their individual probabilities: P(A and B) = P(A) × P(B). The exponent product rule comes into play here, helping to simplify expressions when dealing with multiple events or repeated trials.
Similarly, tree diagrams for probability become invaluable tools when working with independent events. They allow you to visually map out different scenarios and easily identify the paths that lead to specific outcomes. This visual approach can be particularly helpful in understanding how probabilities combine in more complex situations involving multiple independent events.
By solidifying your understanding of these prerequisite topics, you'll be well-equipped to tackle the intricacies of probability of independent events. You'll find that concepts like the multiplication rule and the use of tree diagrams become more intuitive, allowing you to approach probability problems with greater confidence and accuracy. Remember, a strong foundation in these basics is key to mastering more advanced probability concepts in your future studies.

