Parallel line proofs
Topic Notes
Introduction to Parallel Line Proofs
Welcome to the fascinating world of parallel line proofs! These proofs are essential in geometry, helping us understand the relationships between parallel lines and the angles they create. To kick off our journey, we'll start with an introduction video that lays the foundation for this concept. This video is crucial as it visually demonstrates how transversals and parallel lines interact, creating corresponding, alternate, and interior angles. As your math tutor, I'm excited to guide you through this topic. Parallel proofs may seem challenging at first, but with practice, you'll find them quite logical and even enjoyable. They're like solving parallel line puzzles, using what we know about parallel lines to prove other geometric relationships. Remember, mastering parallel line proofs will significantly boost your overall geometry skills. So, let's dive in and explore this fundamental concept together!
Understanding the transversals and parallel lines is key to mastering these proofs. By examining how parallel lines interaction with each other, we can deduce various properties and theorems. Additionally, recognizing the significance of interior angles formed by these lines will aid in solving complex problems. The more you practice, the more intuitive these concepts will become. So, let's continue to explore and enjoy the journey of learning parallel line proofs!
Understanding Parallel Lines and Transversals
Parallel lines and transversals are fundamental concepts in geometry that play a crucial role in understanding spatial relationships. Let's explore these concepts in detail to gain a comprehensive understanding of their properties and applications.
Parallel lines are two or more lines in a plane that never intersect, no matter how far they are extended. These lines maintain a constant distance from each other throughout their length. In mathematical terms, parallel lines have the same slope but different y-intercepts when represented in the coordinate plane. This relationship can be expressed using linear equations, where the general form is y = mx + b, with 'm' representing the slope and 'b' the y-intercept.
For example, consider the lines y = 2x + 3 and y = 2x + 5. Both lines have the same slope (2), but different y-intercepts (3 and 5), making them parallel. Visually, you can imagine these lines as two straight paths that never meet, like railroad tracks stretching into the distance.
Now, let's introduce the concept of a transversal. A transversal is a line that intersects two or more other lines at distinct points. When a transversal crosses parallel lines, it creates fascinating angle relationships that are essential in geometry. Picture a line cutting across two parallel lines, like a diagonal slash across two horizontal lines on a piece of paper.
When a transversal intersects parallel lines, it forms eight angles. These angles can be categorized into pairs with special properties:
- Corresponding angles: These are angles in the same relative position at each intersection. They are always congruent (equal) when the lines are parallel.
- Alternate interior angles: These are angles on opposite sides of the transversal and between the parallel lines. They are also congruent.
- Alternate exterior angles: Similar to alternate interior angles, but outside the parallel lines. These are congruent as well.
- Consecutive interior angles: These are angles on the same side of the transversal and between the parallel lines. They are supplementary, meaning they add up to 180 degrees.
Understanding these angle relationships is crucial for solving geometric problems and proofs. For instance, if you know that two lines are parallel and a transversal creates a 45-degree angle with one of the lines, you can deduce that the corresponding angle on the other parallel line is also 45 degrees.
The concept of parallel lines and transversals extends beyond basic geometry. In real-world applications, these principles are used in architecture for designing buildings with parallel walls, in road construction for planning intersections, and in computer graphics for creating 3D models with consistent spatial relationships.
To visualize these concepts, imagine a ladder leaning against two parallel walls. The rungs of the ladder act as transversals, intersecting both walls at regular intervals. Each rung forms identical angles with both walls, demonstrating the properties of corresponding and alternate angles.
In conclusion, parallel lines and transversals are essential geometric concepts that provide a foundation for understanding more complex spatial relationships. By grasping these principles, students can develop their spatial reasoning skills and apply them to various fields, from mathematics and physics to art and design. The interplay between parallel lines, transversals, and the resulting angle relationships offers a fascinating glimpse into the ordered nature of geometry and its practical applications in our everyday world.
Angle Relationships in Parallel Line Proofs
When a transversal intersects two parallel lines, it creates a fascinating array of angle relationships that are fundamental to geometry. Understanding these relationships is crucial for solving parallel line proofs and mastering more complex geometric concepts. Let's explore the various angle relationships formed in this scenario, focusing on supplementary angles, vertical angles, and their applications in parallel line proofs.
Imagine two parallel lines intersected by a transversal. This configuration creates eight angles, which we can group into pairs based on their relationships. In our example, we'll focus on angles 1, 2, 3, and 4 to illustrate these key relationships.
Supplementary angles are pairs of angles that add up to 180 degrees. In our parallel line scenario, angles on the same side of the transversal and on the same line are always supplementary. For instance, angles 1 and 3 form a supplementary pair, as do angles 2 and 4. This relationship is crucial in parallel line proofs, as it allows us to deduce the measure of one angle if we know the other.
Vertical angles are another important relationship to understand. These are pairs of opposite angles formed when two lines intersect. In our example, angles 1 and 4 are vertical angles, as are angles 2 and 3. A key property of vertical angles is that they are always congruent, meaning they have the same measure. This property is often used as a starting point in parallel line proofs, as it provides a known equality without needing additional information about the parallel lines.
When working with parallel lines intersected by a transversal, we encounter several other angle relationships that are essential for proofs:
1. Corresponding angles: These are angles in the same relative position at each intersection. In our example, angles 1 and 2 are corresponding angles. When lines are parallel, corresponding angles are always congruent.
2. Alternate interior angles: These are angles on opposite sides of the transversal and inside the parallel lines. Angles 3 and 2 form a pair of alternate interior angles. In parallel lines, these angles are always congruent.
3. Alternate exterior angles: Similar to alternate interior angles, but these are outside the parallel lines. While not shown in our 1-2-3-4 example, they follow the same principle of congruence in parallel lines.
4. Same-side interior angles (consecutive interior angles): These are angles on the same side of the transversal and between the parallel lines. Angles 3 and 1 form such a pair. In parallel lines, same-side interior angles are always supplementary.
Understanding these relationships is crucial for constructing parallel line proofs. A typical proof might start with given information about one or more angles and require you to prove a statement about another angle or the parallelism of the lines. The process involves using the known relationships to deduce new information step by step.
For example, if we're given that angle 1 measures 120 degrees and asked to find the measure of angle 3, we can use the supplementary angle relationship. Since angles 1 and 3 are supplementary, we know their sum is 180 degrees. Therefore, angle 3 must measure 60 degrees (180 - 120 = 60).
Similarly, if we know that angle 1 is congruent to angle 2, we can conclude that the lines are parallel because corresponding angles are congruent only when lines are parallel. This forms the basis of many parallel line proofs.
In more complex proofs, you might need to combine multiple relationships. For instance, you might use the fact that vertical angles are congruent to establish that angle 1 equals angle 4, then use the corresponding angle relationship to show that angle 4 equals angle 2, thus proving that angle 1 equals angle 2.
Mastering these angle relationships and their applications in parallel line proofs is essential for advancing in geometry. It provides a foundation for understanding more complex geometric concepts and develops critical thinking skills in mathematical reasoning. By practicing with various scenarios and proofs, students can enhance their ability to visualize and analyze geometric relationships, a skill that extends far
Corresponding Angles in Parallel Lines
Corresponding angles play a crucial role in parallel line proofs, serving as a fundamental concept in geometry. These angles occur when a transversal line intersects two parallel lines, creating a set of angles with special relationships. Understanding corresponding angles is essential for solving complex geometric problems and constructing proofs.
One of the most effective ways to identify corresponding angles is by recognizing the 'F angle' pattern. This pattern resembles the letter F and helps students quickly visualize the relationship between angles. To spot an F angle, look for two parallel lines crossed by a transversal. The angles formed at the points where the transversal intersects the parallel lines create this distinctive F shape.
In the F angle pattern, corresponding angles are located in the same relative position on each parallel line. They form the "top" and "bottom" of the F shape. These angles are always congruent, meaning they have the same measure. This property is fundamental to many geometric proofs involving parallel lines.
When working with parallel line proofs, the corresponding angles relationship can be used in several ways. For example, if you know that two lines are parallel and a transversal intersects them, you can conclude that the corresponding angles are congruent. Conversely, if you can prove that corresponding angles are congruent, you can deduce that the lines intersected by the transversal are parallel.
Here's a practical example: Imagine two parallel lines, l and m, intersected by a transversal t. Angle A is formed where t intersects l, and angle B is formed where t intersects m in the corresponding position. If you're given that angle A measures 45°, you can conclude that angle B also measures 45° because they are corresponding angles.
In more complex proofs, you might need to use the corresponding angles relationship in combination with other angle relationships, such as alternate interior angles or vertical angles. By recognizing these patterns and understanding their properties, you can navigate through multi-step proofs more efficiently.
Visualizing these angle patterns is key to solving problems involving parallel lines. Practice identifying F angles in various diagrams and real-world situations to strengthen your geometric intuition. As you become more familiar with these patterns, you'll find it easier to spot relationships and formulate proofs.
Remember, the power of the F angle concept lies in its simplicity and visual nature. It provides a quick and reliable method for identifying corresponding angles without the need for complex calculations. By mastering this visualization technique, you'll be better equipped to tackle a wide range of geometric problems and proofs involving parallel lines.
In conclusion, corresponding angles and the F angle pattern are essential tools in the geometry toolkit. They offer a straightforward approach to understanding and proving relationships in parallel line configurations. By honing your ability to recognize these patterns, you'll enhance your problem-solving skills and develop a deeper appreciation for the elegant logic of geometric proofs. Whether you're a student studying for exams or an enthusiast exploring the beauty of mathematics, mastering corresponding angles will undoubtedly enrich your geometric understanding and capabilities.
Alternate Interior and Exterior Angles
Understanding alternate exterior angles is crucial when working with parallel line proofs in geometry. These angle relationships form the foundation for more complex geometric proofs and are essential concepts for students to master.
Alternate interior angles are pairs of angles that lie on opposite sides of a transversal and between two parallel lines. They are always congruent, meaning they have the same measure. This relationship is often visualized using the 'Z pattern.' Imagine drawing a 'Z' shape across the parallel lines, with the middle line of the 'Z' being the transversal. The angles at the ends of this 'Z' are the alternate interior angles.
For example, consider two parallel lines cut by a transversal. The angles formed on the inner side of the parallel lines, on opposite sides of the transversal, are alternate interior angles. If we label these angles as angle A and angle B, we can state with certainty that angle A is congruent to angle B.
Alternate exterior angles, on the other hand, are pairs of angles that lie on opposite sides of a transversal and outside the two parallel lines. Like alternate interior angles, alternate exterior angles are also congruent. However, the visual pattern for identifying these angles differs slightly from the 'Z pattern' used for interior angles.
To identify angle relationships, imagine an elongated 'C' shape or a backwards 'C' shape that extends outside the parallel lines. The angles at the ends of this 'C' shape are the alternate exterior angles. This pattern helps students quickly recognize and work with these angle relationships in proofs.
For instance, if we have two parallel lines intersected by a transversal, the angles formed on the outer side of the parallel lines, on opposite sides of the transversal, are alternate exterior angles. Let's call these angles C and D. We can confidently state that angle C is congruent to angle D.
The importance of understanding these angle relationships cannot be overstated when it comes to solving more complex geometric proofs. Many proofs involving parallel lines and transversals rely on the properties of alternate interior and exterior angles. By recognizing these relationships, students can make logical deductions and construct valid arguments in their proofs.
For example, in a proof where you need to show that two angles are congruent, you might use the fact that they are alternate interior angles of parallel lines as a key step in your reasoning. Similarly, knowing that alternate exterior angles are congruent can help you establish relationships between angles in more complex figures.
It's also worth noting that these angle relationships work in reverse. If two lines are cut by a transversal and the alternate interior angles are congruent, we can conclude that the lines are parallel. The same is true for proving lines are parallel. This property is often used in proofs where parallelism needs to be established.
To reinforce these concepts, practice identifying angle relationships in various diagrams. Try creating your own parallel line configurations and labeling the different angle pairs. As you work through proofs, make a habit of looking for these relationships and consider how they might be useful in your logical arguments.
Remember, the 'Z pattern' for alternate interior angles and the 'C pattern' for alternate exterior angles are valuable visual aids, but they're not just tricks for memorization. They represent fundamental geometric truths that form the basis of many theorems and proofs. By internalizing these concepts, you'll be better equipped to tackle a wide range of geometric problems and proofs involving parallel lines and transversals.
Co-Interior Angles and Other Relationships
Co-interior angles, also known as interior angles on the same side of the transversal, play a crucial role in geometry, particularly in parallel line proofs. These angles occur when a transversal line intersects two other lines, creating a set of eight angles. Understanding co-interior angles and their properties is essential for solving complex geometric problems and proofs.
By definition, co-interior angles are pairs of angles that lie on the same side of the transversal and are inside the two lines being intersected. These angles have a special relationship: they are always supplementary, meaning they sum to 180 degrees. This property is fundamental in parallel line geometry and is often used as a key step in proofs involving parallel lines.
The supplementary nature of co-interior angles can be explained by the parallel postulate and the properties of straight lines. When two parallel lines are cut by a transversal, the alternate interior angles are congruent. This congruence, combined with the fact that angles on a straight line sum to 180 degrees, leads to the conclusion that co-interior angles must be supplementary.
To identify co-interior angles, look for two angles that are on the same side of the transversal and between the two intersected lines. These angles will always be non-adjacent, separated by the transversal. In a typical diagram, you'll find two pairs of co-interior angles: one pair above the top line and another below the bottom line.
The relationship between co-interior angles is particularly useful in parallel line proofs. If you can prove that a pair of co-interior angles are supplementary, you can conclude that the two lines intersected by the transversal are parallel. Conversely, if you know that two lines are parallel, you can deduce that the co-interior angles formed by any transversal will be supplementary.
While co-interior angles are a key concept, they are just one of several important angle relationships in parallel line geometry. Other significant relationships include:
1. Corresponding angles: These are angles in matching positions relative to the transversal and the two intersected lines. In parallel lines, corresponding angles are always congruent.
2. Alternate interior angles: These angles lie on opposite sides of the transversal and between the two lines. In parallel lines, alternate interior angles are congruent.
3. Alternate exterior angles: Similar to alternate interior angles, but these lie outside the two lines. They are also congruent when the lines are parallel.
4. Vertical angles: These are opposite angles formed by two intersecting lines. Vertical angles are always congruent, regardless of whether the intersected lines are parallel.
Understanding these relationships is crucial for solving more complex geometric problems and constructing proofs. For instance, if you can prove that alternate interior angles are congruent, you can conclude that the lines are parallel. Similarly, if corresponding angles are congruent, the lines must be parallel.
In parallel line proofs, these angle relationships are often used in combination. You might start by identifying a pair of congruent corresponding angles, then use that information to deduce something about co-interior angles or alternate interior angles. The ability to recognize and apply these relationships flexibly is key to success in geometric reasoning and proof-writing.
It's worth noting that while these angle relationships are most commonly discussed in the context of parallel lines, they can also be applied to non-parallel lines. In such cases, the relationships change predictably, providing valuable information about the geometry of the situation. For example, if co-interior angles sum to less than 180 degrees, the lines will intersect on that side of the transversal.
Mastering the concept of co-interior angles and related angle relationships is fundamental to understanding parallel line geometry. These principles form the foundation for more advanced geometric concepts and are essential tools in mathematical problem-solving and proof construction. By thoroughly grasping these relationships, students can develop a strong intuition for geometric reasoning, enabling them to tackle more complex problems with confidence and precision.
Applying Parallel Line Proofs in Problem Solving
Mastering parallel line proofs is essential for success in geometry. These proofs require a systematic approach and a keen eye for geometric relationships. To effectively solve parallel line proof problems, follow these guidelines and apply the concepts you've learned.
First, carefully analyze the given information and diagram. Look for key relationships between angles and lines, paying special attention to parallel lines and transversals. Identify any corresponding angles, alternate interior angles, or alternate exterior angles, as these often play crucial roles in parallel line proofs.
Use visual cues to your advantage. Highlight parallel lines with arrows or different colors to make them stand out. Mark congruent angles with matching symbols or colors. This visual organization can help you quickly spot important relationships and potential proof steps.
When structuring your proof, start by clearly stating the given information and what you need to prove. Then, list your steps in a logical order, providing a reason for each statement. Remember to use theorems and postulates related to parallel lines, such as the Alternate Interior Angles Theorem or the Corresponding Angles Postulate.
Here's a simple example to demonstrate these concepts:
Given: Lines l and m are parallel, and line n is a transversal.
Prove: Angle 1 is congruent to Angle 2
Proof:
1. Lines l and m are parallel (Given)
2. Line n is a transversal (Given)
3. Angle 1 and Angle 3 are alternate interior angles (Definition of alternate interior angles)
4. Alternate interior angles are congruent when lines are parallel (Alternate Interior Angles Theorem)
5. Therefore, Angle 1 is congruent to Angle 3 (Steps 3 and 4)
6. Angle 2 and Angle 3 are vertical angles (Definition of vertical angles)
7. Vertical angles are congruent (Vertical Angles Theorem)
8. Therefore, Angle 2 is congruent to Angle 3 (Steps 6 and 7)
9. If two angles are congruent to the same angle, they are congruent to each other (Transitive Property)
10. Therefore, Angle 1 is congruent to Angle 2 (Steps 5, 8, and 9)
As you practice more parallel line proofs, you'll develop a better intuition for identifying key relationships and structuring your arguments. Remember to always justify each step with a valid reason, and don't hesitate to use auxiliary lines or extend existing lines if it helps you see additional relationships. With consistent practice and application of these problem-solving strategies, you'll become proficient in tackling even the most challenging parallel line proof problems in geometry.
Conclusion and Further Practice
In this article, we've explored the essential concepts of parallel line proofs in geometry. We've covered the fundamental theorems, including corresponding angles, alternate interior angles, and same-side interior angles. The introduction video provided a crucial foundation for understanding these proofs, demonstrating how to apply logical reasoning to geometric relationships. To truly master parallel line proofs, regular practice is key. Try solving various problems, starting with simpler examples and gradually increasing complexity. Explore online geometry resources, such as Khan Academy or GeoGebra, for interactive exercises. Consider joining math forums or study groups to discuss challenging proofs with peers. Remember, proficiency in parallel line proofs not only enhances your geometry skills but also strengthens your overall mathematical reasoning abilities. As you continue your geometry journey, these concepts will serve as building blocks for more advanced topics. Keep practicing, stay curious, and enjoy the logical beauty of same-side interior angles!
Parallel Line Proofs: Finding the Value of x
What is the value of x if ?
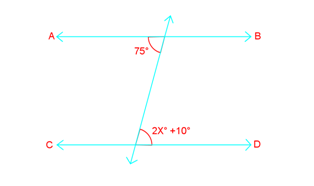
Step 1: Understanding the Problem
In this problem, we are given two parallel lines, and , and a transversal line that intersects these parallel lines. The goal is to find the value of given the angles formed by the transversal and the parallel lines.
Step 2: Identifying the Given Information
We are provided with the following information:
- is parallel to .
- There is a transversal line intersecting these parallel lines.
- One of the angles formed by the transversal and the parallel lines is .
- The other angle formed by the transversal and the parallel lines is expressed as .
Step 3: Applying the Alternate Interior Angles Theorem
According to the Alternate Interior Angles Theorem, when a transversal intersects two parallel lines, the pairs of alternate interior angles are congruent. This means that the angle measuring is congruent to the angle measuring .
Step 4: Setting Up the Equation
Since the alternate interior angles are congruent, we can set up the following equation:
Step 5: Solving for x
To find the value of , we need to solve the equation:
- First, subtract 10 from both sides of the equation to isolate the term with :
- Next, divide both sides by 2 to solve for :
Step 6: Verifying the Solution
To ensure our solution is correct, we can substitute back into the expression for the angle:
Since the calculated angle matches the given angle of , our solution is verified.
Conclusion
By applying the Alternate Interior Angles Theorem and solving the resulting equation, we have determined the value of . This step-by-step approach ensures a clear and accurate solution to the problem.
FAQs
Here are some frequently asked questions about parallel line proofs:
1. What are the 5 ways to prove that lines are parallel?
The five main ways to prove lines are parallel are: 1) Corresponding angles are congruent 2) Alternate interior angles are congruent 3) Alternate exterior angles are congruent 4) Same-side interior angles are supplementary 5) Two lines perpendicular to the same line are parallel
2. How do you prove that lines are parallel?
To prove lines are parallel, you need to show one of the following: - Corresponding angles are congruent - Alternate interior angles are congruent - Same-side interior angles are supplementary Use given information and geometric theorems to logically prove one of these conditions.
3. How do you prove equations are parallel?
To prove equations represent parallel lines: 1) Write equations in slope-intercept form (y = mx + b) 2) Compare the slopes (m values) 3) If slopes are equal, the lines are parallel Remember, parallel lines have the same slope but different y-intercepts.
4. How do you prove if two lines are parallel or not?
To prove if lines are parallel: 1) Check if corresponding or alternate interior angles are congruent 2) Verify if same-side interior angles are supplementary 3) Compare slopes if equations are given 4) Use the transitive property if both lines are parallel to a third line If any of these conditions are met, the lines are parallel.
5. What is the proof statement for parallel lines?
A typical proof statement for parallel lines is: "Given: (State given information about angles or lines) Prove: Line AB is parallel to Line CD" The proof then uses logical steps and geometric theorems to show that one of the conditions for parallel lines is satisfied.
Prerequisite Topics for Parallel Line Proofs
Understanding parallel line proofs is a crucial skill in geometry, but to master this concept, it's essential to have a solid foundation in several prerequisite topics. One of the most fundamental prerequisites is parallel lines and transversals. This topic introduces the key relationships between parallel lines and the angles formed when they are intersected by a transversal, which is the cornerstone of many parallel line proofs.
Another important prerequisite is the study of polygons. While it might not seem directly related, understanding polygons helps in visualizing and applying concepts like the alternate interior angles theorem, which is frequently used in parallel line proofs. This knowledge allows students to recognize and utilize angle relationships within more complex geometric figures.
Surprisingly, conics and circles also play a role in preparing for parallel line proofs. This topic introduces students to linear equations in the coordinate plane, which is crucial for understanding how parallel lines are represented algebraically and graphically. This algebraic perspective is often essential in more advanced parallel line proofs.
The concept of parallel and perpendicular lines in linear functions is directly relevant to parallel line proofs. This prerequisite topic provides the tools for proving lines are parallel using algebraic methods, complementing the geometric approaches and offering alternative proof strategies.
Lastly, while it might seem unrelated at first glance, combination of SohCahToa questions can be beneficial. This topic enhances students' ability in visualizing angle patterns, which is invaluable when working with complex parallel line configurations in proofs.
By mastering these prerequisite topics, students build a strong foundation for tackling parallel line proofs. Each topic contributes unique skills and perspectives: from understanding basic angle relationships and polygon properties to applying algebraic concepts and enhancing spatial visualization. This comprehensive background enables students to approach parallel line proofs with confidence, armed with a diverse set of tools and strategies.
Remember, geometry is a subject where concepts build upon each other. Skipping or glossing over these prerequisites can lead to difficulties in understanding and applying the principles of parallel line proofs. Therefore, it's crucial to invest time in thoroughly grasping these foundational topics. Doing so will not only make parallel line proofs more accessible but will also enhance overall geometric reasoning skills, setting students up for success in more advanced geometric concepts.

