Point Slope Form
What is Point Slope Form?
The point slope form (sometimes known as point-gradient form) is one of the three forms we can use to express a straight line. This form is useful because we can determine the equation of the line by simply knowing a single point on the line and the slope of the line. The other forms are called slope intercept form and standard form, but we will mostly be using slope point form in this section.
How to write point slope form?
Using this point slope form formula (or point gradient formula), we express the equation of a line to be:
You may know x and y to be variables of the equation, but what are , and m?
What is and ?
The terms and are numbers which represent the x-coordinate and y-coordinates of a point on a line. For example, let's look at this line on the coordinate plane.

Notice that the point (1,0) is on the line. We see that the 1 represents the x-coordinate of the point, and 0 represents the y-coordinate. So we can conclude that
However, take note that the point (0,-1) is also on the line. Does that mean we used the wrong point? The answer is no! You can also use this point to represent and . In other words, we can also say that:
In general, we are allowed to use and to represent x- and y- coordinates of any known point on the line. However, do not confuse and withx and y. The letters x and y are variables that can represent any point on the line, whereas and are numbers that represents one specific known point on the line. Luckily, x and y when not something we have to solve when dealing with the point slope equation. So don't worry about it too much!
How to find a slope of a line?
The letter m in the point slope form equation is a number that represents the slope of the line. Some people refer to the slope as rise over run. Recall that if we have two points, then we are able to find the slope of the two points by using the slope formula.
The same idea works here. If we take any two points on a straight line, then we can find the slope of the line using the above formula! For example, let's use this line.
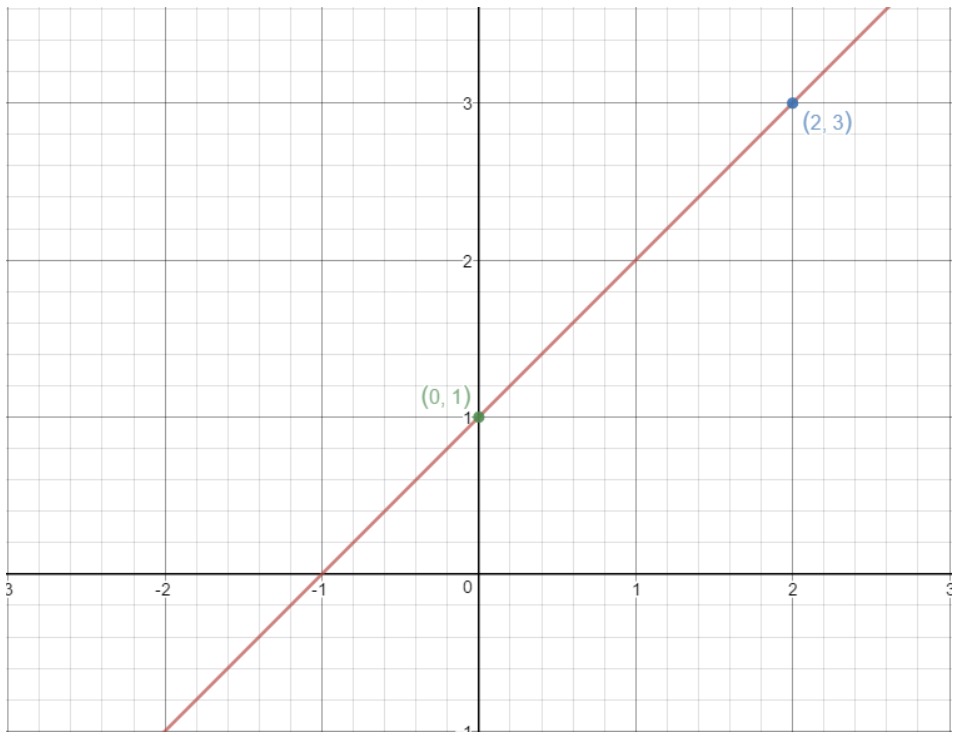
Notice the points (2, 3) and (0, 1) are on this graph. So why don't we use these two points to find the slope of the line? Using the formula, we would get:
That means the slope of this line is 1!
One important thing to remember is that we can assign any of the two points to be point 1 or point 2 – as long as we keep it consistent. In other words, if we assign the point (2, 3) as point 1, both its x- and y-coordinates should be and . However, if we assign it to be point 2, both its its x- and y-coordinates should be and .
You can also use the rise over run concept here as well. To go from the point (0, 1) to (2, 3), we have to go 2 units right and 2 units up. That means rise is 2 and run is 2, thus = 1.
How to graph point slope form?
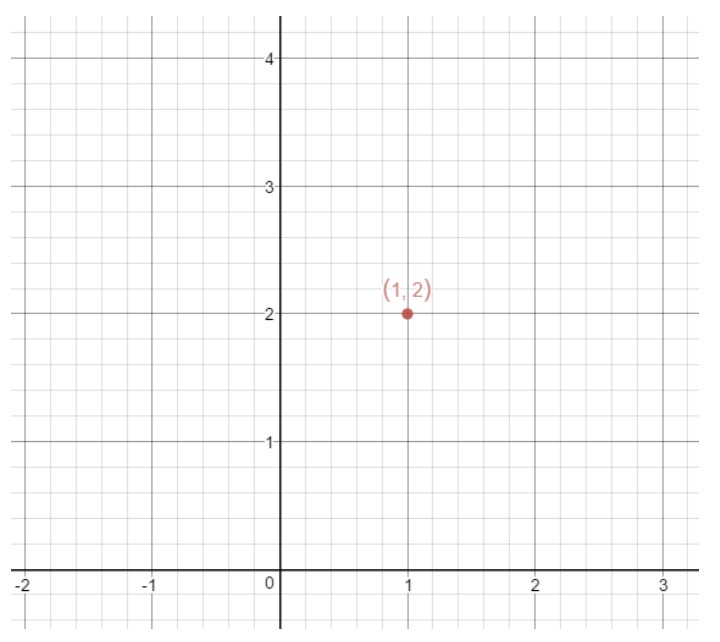
We may know the equation very well, but how exactly do we use the equation to graph the line? Well let's look an example of the following point slope from equation:
From looking at the equation, we see that:
This means that the point (1,2) is on the line, and the slope of the line is 2. Drawing on the point on the coordinate plane gives us the following graph.
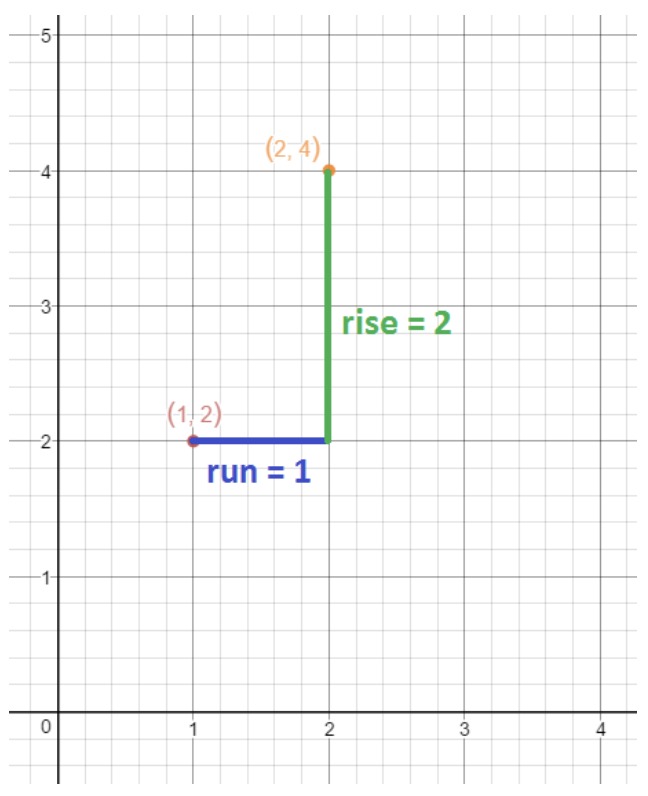
How are we supposed to use the slope of the line to draw the line itself? Well, remember that
We know the slope is 2. The number 2 is the same as . Hence,
The equation tells us that the rise is 2, and the run is 1. This means if I were to go one unit right and two units up from the point (1,2), then I will get another point on the line. This point will be (2,4). Plotting this on the coordinate plane gives:
Now all we have to do is draw a straight line that intersects these two points. This gives us the following line.
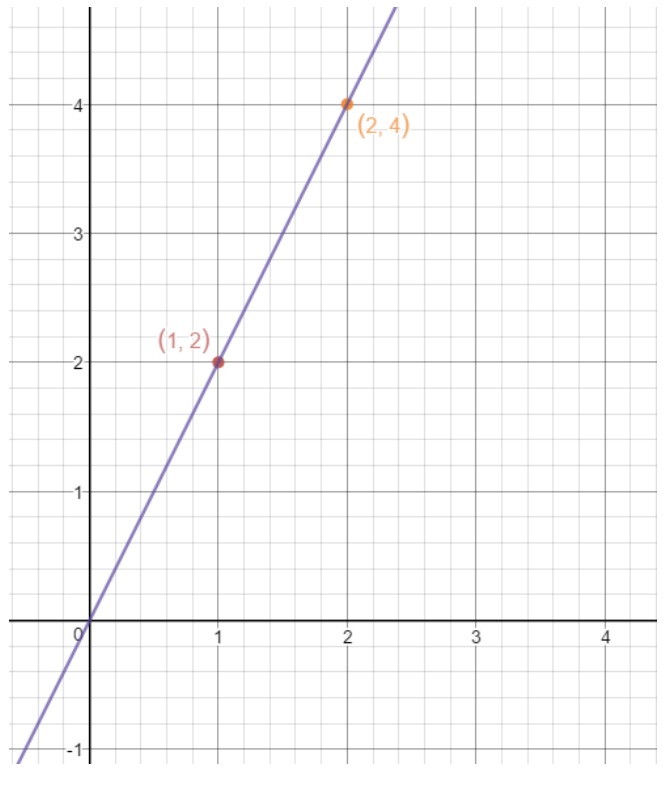
Now that we know the slope and the point slope form equation really well, why don't we look at specific questions about finding them?
Find equation of a line given point and slope
Question 1: Given the point (3,7) and the slope = -1, find the equation in slope-point form.
Recall that the point slope formula is:
We know the point (3, 7) is the x-coordinate and y-coordinate of a single point, and the slope is -1. Hence we have the following information:
Plugging these into our point slope equation gives:
We don't have to look for x and y, so we are finished! Now let's do a harder problem.
Question 2: Given the point (2,-1) and the slope = 0, find the equation in slope-point form.
We know the point (2, -1) is the x-coordinate and y-coordinate of a single point, and the slope is 0. Hence we have the following information:
Plugging these into our point slope equation gives:
Notice on the right hand side of the equation that we are multiplying by 0. So we have:
There is nothing left for us to do except to move the -7 to the right side of the equation. This gives us the final result:
If you were to draw this line, then you would get a horizontal line that intersects the y-intercept at 7. Why is the line horizontal? Well, notice that
The run could be any number #, but the rise is 0. That means the line will never rise at all, and it will run infinitely. So if it only runs, then you will end up getting a straight line that is horizontal. Let's look at one more question of this section.
Question 3: Given the point (-3,5) and the slope , find the equation in slope-point form.
We know the point (-3, 5) is the x-coordinate and y-coordinate of a single point, and an undefined slope. Hence we have the following information:
Normally we would want to look the stuff we found right away into the equation. However, m is undefined! So how are we supposed to plug that m into the equation? Let's start off with plugging on the x-coordinate and y-coordinate into the equation. This gives us:
We are going to isolate for the letter m here. Dividing both sides of the equation by x + 3 gives:
Now let's ask ourselves the question: when does m become undefined? It becomes undefined if we divide a number no. by 0. In other words,
Now combining these two equations give us:
See that the numerators of both fractions don't really tell us anything. However, if we match the denominators of the fractions, then we get:
Moving the 3 to the right hand side gives us the final result:
If you were to draw this line, you would get a vertical line that intersects the x-axis at -3. The line is vertical because the run is 0. Hence the line rises infinitely, causing the line to go straight up. Now let's look at some questions which require us to use two points on a coordinate plane.
Finding slope from two points
Question 4: Given two points (2, 1) and (-6, 9), find the slope of the line.
Recall that to find the slope of the line, we use the slope equation
Hence using this formula gives us:
Question 5: Given two points (3,3) and (7,3), find the slope of the line.
Again, using the slope formula gives us the following:
Hence, we conclude that the slope is 0. Let's do one more.
Question 6: Given two points (-4,1) and (-4,3), find the slope of the line.
Using the slope formula gives us:
The slope is undefined because we are dividing by zero!
Finding the variable given two points and the slope
So finding the slope from two points is actually pretty easy. However, what if one of the points has a variable in it? What would that variable be? Let's look at an example.
Question 7: Given the slope and two points on a line (-3,-4) and (2,a), find the value of a.
Notice that the point (2,a) has the letter a in the y-coordinate. We are going to have to find this variable. Recall that to find the slope of the line, we use the slope equation
From the question, we are given the following information:
If we were to plug these into the slope formula , we will get:
Notice that within this equation, we can solve for by isolating it. Multiplying both sides by 5 gives:
Subtracting both sides of the equation by 4 gives the final result:
which is the value of a. Now what if a point contains the variable a in both the x-coordinate and y-coordinate?
Question 8: Given the slope and two points on a line (3,4) and (a - 2,a), find the value of a.
Again, we will be using the slope formula
From the question, we are given the following information:
So plugging these into the slope formula gives us:
Now we are going isolate a again. Cross multiplying gives us:
Adding both sides of the equation by 8 gives:
Subtracting both sides of the equation by a gives us the final result:
Hence the value of a is 3.
The whole time we have been looking at slopes. However, what if I have to find the equation of a line in slope point form from the two points?
Equation of a line given two points
Question 9: Given two points (-6,1) and (2,6), find the point slope form equation.
Recall that the point slope form equation is . As you can tell, we are going to need to find and m. Notice that we can find the slope by using the slope formula with these two points. So,
To find and , we can simply take one of the points given in the question. Let's take the point (2, 6). Hence we can say that:
Plugging and into the point slope equation gives us:
Now we know how to find an equation of a line when given to points, but what if we are given a graph?
Finding the equation of a line from a graph
Question 10: Find the equation of a line with the following graph:
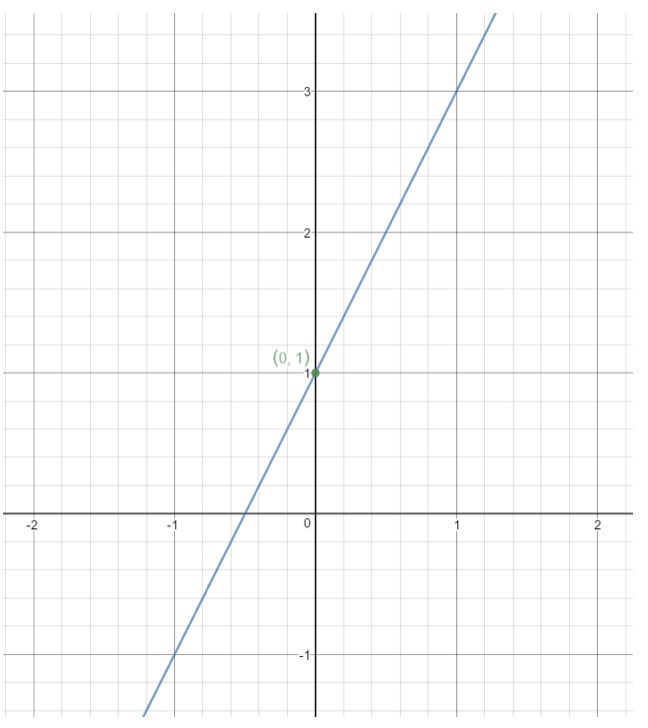
Remember the equation of the line in point slope form is .
Notice here that the point (0,1) is on the line. This means we can set:
Now we need to find the slope. Recall that the slope formula is:
Our goal is to look at the graph and find out how much I need to run, and how much I need to rise to get to the next point on the line. There are multiple ways to do this, but we will do it this way.
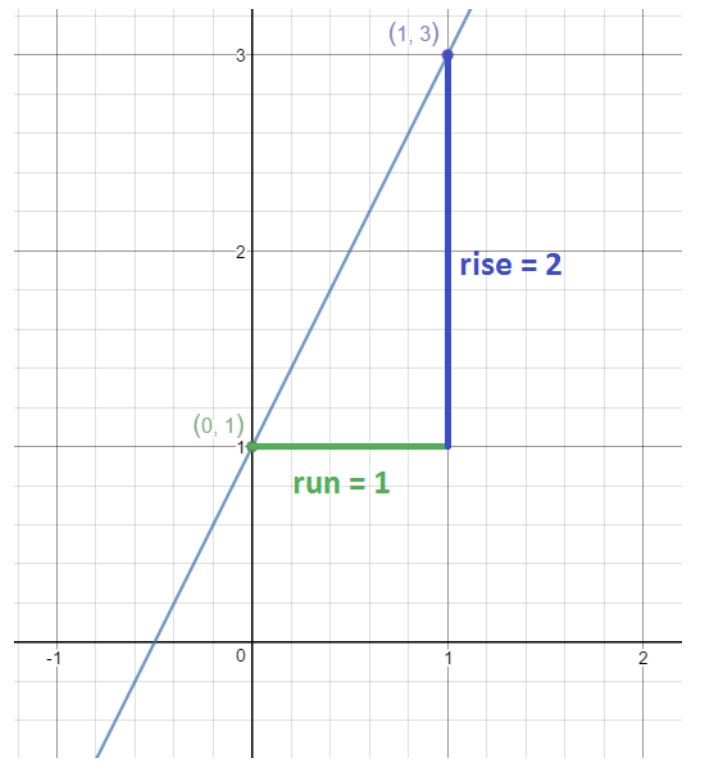
Here we see that if we were to move 1 unit to the right and 2 units up, then that will lead us to the point (1,3). This point is on the line, so we know the amount of units we moved right and up are correct. We know that moving to the right by 1 means the run is equal to 1, and moving up 2 means the rise is 2. Hence, we conclude
So the slope is 2. Thus, we finalize the point slope equation to be:
If you are still having trouble visualizing the equation of a line, we recommend you to check the program at the bottom of this page.
http://zonalandeducation.com/mmts/functionInstitute/linearFunctions/newLpsf/lpsf0.php
This program lets you change the point and the slope of the line. With each change you make, you will get a different type of line. Play around with it and watch how the line changes!







