Congruence and congruent triangles
Topic Notes
Introduction to Congruence and Congruent Triangles
Congruence is a fundamental concept in geometry, particularly when studying triangles. Congruent triangles are identical in shape and size, with corresponding angles and sides equal. Our introduction video provides a visual explanation of this concept, serving as a crucial foundation for understanding congruence. This lesson will delve into various methods to prove triangle congruence, including Side-Side-Side (SSS), Side-Angle-Side (SAS), and Angle-Side-Angle (ASA). These proofs are essential tools in geometry, allowing us to establish relationships between different triangles and solve complex problems. By mastering congruence, students can tackle more advanced geometric concepts and apply their knowledge to real-world situations, such as architecture and engineering. Throughout this lesson, we'll explore practical applications of congruent triangles, demonstrating how this seemingly abstract concept plays a vital role in our everyday lives and various professional fields.
Understanding the concept of corresponding angles and sides is crucial for solving problems related to congruent triangles. These problems often require students to identify and compare different parts of triangles to determine congruence. By practicing these skills, students can develop a deeper understanding of geometric principles and improve their problem-solving abilities. Additionally, the knowledge of congruent triangles and their properties can be applied to various real-world scenarios, making it a valuable topic in both academic and professional contexts.
Understanding Congruence in Triangles
Congruence is a fundamental concept in geometry, particularly when it comes to triangles. In the context of triangles, congruence refers to the property of two or more triangles being identical in both shape and size. This means that if you were to place one triangle on top of another congruent triangle, they would match up perfectly, with all corresponding sides and angles being equal.
When we talk about congruent triangles, it's crucial to understand the concept of corresponding parts. These are the elements of the triangles that match up when the triangles are congruent. Corresponding parts include:
- Corresponding sides: The lengths of matching sides are equal
- Corresponding angles: The measures of matching angles are equal
- Corresponding vertices: The points where sides meet in each triangle
To illustrate this concept, imagine two triangles, ABC and DEF. If these triangles are congruent, we can say that:
- Side AB corresponds to side DE
- Side BC corresponds to side EF
- Side AC corresponds to side DF
- Angle A corresponds to angle D
- Angle B corresponds to angle E
- Angle C corresponds to angle F
Understanding congruence is essential in solving geometry problems. When we can prove that two triangles are congruent, we gain valuable information about all parts of both triangles. This knowledge allows us to:
- Determine unknown side lengths or angle measures
- Prove relationships between different parts of geometric figures
- Simplify complex geometric proofs
- Apply triangle congruence to real-world problems in engineering and design
There are several methods to prove triangle congruence, including:
- Side-Side-Side (SSS): All three sides of one triangle are equal to the corresponding sides of another triangle
- Side-Angle-Side (SAS): Two sides and the included angle of one triangle are equal to the corresponding parts of another triangle
- Angle-Side-Angle (ASA): Two angles and the included side of one triangle are equal to the corresponding parts of another triangle
- Angle-Angle-Side (AAS): Two angles and a non-included side of one triangle are equal to the corresponding parts of another triangle
By mastering the concept of congruence in triangles, students can develop a strong foundation for more advanced geometric concepts and problem-solving techniques. The ability to recognize and prove congruence allows for efficient solutions to complex geometric problems, making it an invaluable skill in mathematics and related fields.
Understanding congruence is essential in solving geometry problems. When we can prove that two triangles are congruent, we gain valuable information about all parts of both triangles. This knowledge allows us to:
Side-Side-Side (SSS) Congruence
The Side-Side-Side (SSS) congruence theorem is a fundamental principle in geometry that allows us to prove two triangles are congruent if all three corresponding sides are equal. This powerful theorem simplifies many geometric proofs and problem-solving scenarios. To understand SSS congruence, let's delve into its definition, application, and significance.
SSS congruence states that if three sides of one triangle are congruent to three sides of another triangle, then the two triangles are congruent. This means that not only are the sides equal, but the corresponding angles are also equal. The beauty of this theorem lies in its simplicity we only need to prove the equality of sides to establish complete congruence.
Let's consider an example to illustrate how SSS congruence works:
Imagine we have two triangles, ABC and DEF. We know that:
- AB = DE
- BC = EF
- AC = DF
Given this information, we can conclude that triangle ABC is congruent to triangle DEF using the SSS congruence theorem. This means that not only are the sides equal, but the corresponding angles (A = D, B = E, C = F) are also equal.
Here's a simple diagram to visualize this concept:
The SSS congruence theorem works because the length of the sides of a triangle uniquely determines its shape and size. If we have three rigid rods of specific lengths, there's only one way to arrange them to form a triangle. This uniqueness is what allows us to prove congruence based solely on side lengths.
This method is particularly useful in problem-solving scenarios where we have information about side lengths but lack angle measurements. It's commonly applied in construction, engineering, and various geometric proofs. For instance, in bridge design, ensuring that support structures on both sides have congruent triangular formations is crucial for stability and load distribution.
The SSS congruence theorem is one of several methods to prove triangle congruence, alongside Side-Angle-Side (SAS) and Angle-Side-Angle (ASA). Each has its specific applications, but SSS is often the go-to when dealing with problems that provide side length information. By mastering this theorem, students and professionals alike can tackle a wide range of geometric challenges with confidence and precision.
Side-Angle-Side (SAS) Congruence
The Side-Angle-Side (SAS) congruence theorem is a fundamental principle in geometry that allows us to prove two triangles are congruent. According to this theorem, if two sides and the included angle of one triangle are equal to the corresponding sides and angles of another triangle, then the two triangles are congruent. The included angle is the angle formed between the two given sides.
To visualize this, imagine two triangles, ABC and DEF. If AB = DE, BC = EF, and angle B = angle E (where B and E are the included angles), then triangle ABC is congruent to triangle DEF. This can be represented in a diagram showing the two triangles side by side, with the equal parts clearly marked.
The SAS congruence theorem is valid because these three pieces of information (two sides and the included angle) uniquely determine the shape and size of a triangle. Once these elements are fixed, there is only one possible way to complete the triangle, ensuring that all other corresponding sides and angles will be equal.
SAS differs from the SSS (Side-Side-Side) congruence theorem in a crucial way. While SSS requires all three sides of the triangles to be equal, SAS only needs two sides and the angle between them. This makes SAS particularly useful in situations where we have information about an angle but not all sides.
The SAS congruence theorem is especially valuable in various geometry problems and real-world applications. For instance, in surveying and mapping, SAS can be used to determine distances or positions when direct measurements are not possible. In construction and engineering, it helps in verifying the congruence of structural elements or in designing symmetrical structures.
Moreover, SAS is often employed in proofs involving overlapping triangles or in problems where rotations and reflections are involved. It's a powerful tool for solving complex geometric puzzles and for establishing the congruence of triangles in more intricate figures.
Understanding and applying the SAS congruence theorem is essential for students and professionals alike. It not only simplifies many geometric proofs but also enhances spatial reasoning skills. By mastering this theorem, one gains a deeper appreciation for the logical structure of geometry and its practical applications in various fields.
Angle-Side-Angle (ASA) and Angle-Angle-Side (AAS) Congruence
In the realm of geometry, understanding triangle congruence is crucial. Two essential theorems that help us prove triangle congruence are the Angle-Side-Angle (ASA) and Angle-Angle-Side (AAS) congruence theorems. These powerful tools allow us to determine if two triangles are congruent without having to check all six parts (three sides and three angles) of each triangle.
Angle-Side-Angle (ASA) Congruence
The ASA congruence theorem states that if two angles and the included side of one triangle are congruent to the corresponding parts of another triangle, then the triangles are congruent. Here's a visual representation:
In this diagram, if A D, AB DE, and B E, then ABC DEF. The ASA theorem works because once we have two angles and the side between them, the third angle is determined (since the sum of angles in a triangle is always 180°), and the other two sides are fixed by the given information.
Angle-Angle-Side (AAS) Congruence
The AAS congruence theorem states that if two angles and a non-included side of one triangle are congruent to the corresponding parts of another triangle, then the triangles are congruent. Here's a visual representation:
In this diagram, if A D, B E, and BC EF, then ABC DEF. The AAS theorem works for similar reasons as ASA. With two angles known, the third is determined, and the given side fixes the size of the triangle.
Comparing ASA vs AAS
Both ASA and AAS congruence theorems are based on the principle of corresponding parts of congruent triangles being congruent (CPCTC). The key difference lies in the position of the given side:
- In ASA, the given side is between the two known angles.
- In AAS, the given side is not between the two known angles.
Both theorems work because they provide enough information to uniquely determine the shape and size of a triangle. Once we know two angles, the third is automatically determined. The given side then fixes the scale of the triangle.
When to Use ASA vs AAS
The choice between using ASA or AAS in problem-solving depends on the given information:
- Use ASA when you have two angles and the side between them.
- Use AAS when you have two angles and a side that's not between them.
For example, in a problem where you're given two angles of a triangle and the side opposite one of those angles, you'd use AAS. If you're given two angles and the side adjacent to both, you'd use ASA.
Relationship to Corresponding Parts
The concept of corresponding parts is fundamental to both ASA and AAS congruence. When we prove triangles congruent using these theorems, we're essentially saying that all corresponding parts of the triangles are congruent. This means:
- Corresponding angles are congruent
- Corresponding sides are congruent
Once we establish congruence using ASA or AAS, we can confidently state that all other corresponding parts of the triangles are also congruent.
The Ambiguous Case: Side-Side-Angle (SSA)
Side-Side-Angle (SSA) is not a valid congruence proof in general due to the ambiguous case that can arise when attempting to construct a triangle using this combination of information. Unlike the reliable Side-Angle-Side (SAS) or Side-Side-Side (SSS) congruence theorems, SSA can lead to multiple possible triangles, making it unreliable for proving congruence in most situations.
To understand why SSA is problematic, let's visualize the ambiguous case. Imagine we're given two sides and a non-included angle of a triangle. When we try to construct this triangle, we may end up with two different possible triangles that satisfy the given conditions. This occurs because the third side can intersect the circle (drawn with the radius of the second given side) at two points, creating two distinct triangles.
For example, consider a triangle with side lengths of 5 and 7 units, and an angle of 30° opposite the side of length 5. When we attempt to construct this triangle, we find that there are two possible configurations that satisfy these conditions. This ambiguity is why SSA cannot be relied upon for proving congruence in general cases.
However, there is an important exception to this rule: the hypotenuse-leg theorem for right triangles. In a right triangle, if we know the hypotenuse and one leg, we can indeed prove congruence. This is because the right angle eliminates the possibility of multiple triangles fitting the given information. The hypotenuse-leg theorem is sometimes referred to as the HL congruence theorem and is a valid method for proving congruence in right triangles specifically.
Understanding the limitations of SSA and the exception for right triangles is crucial in geometry problem-solving. When approaching triangle congruence proofs, students and mathematicians must be aware that SSA is not a reliable method in most cases. Instead, they should look for opportunities to use SAS, SSS, or other valid congruence theorems. Recognizing the potential for ambiguity in SSA situations can prevent errors in geometric reasoning and proofs.
In conclusion, while SSA is not generally valid for proving congruence due to the ambiguous case, it's essential to remember the hypotenuse-leg theorem as a special case for right triangles. This knowledge enhances problem-solving skills and deepens understanding of geometric principles, allowing for more accurate and confident navigation of triangle congruence problems in various mathematical contexts.
Applying Congruence Proofs in Geometry Problems
Congruence proofs are powerful tools in solving geometry problems, offering efficient methods to deduce information about unknown angles and sides in complex geometric figures. This guide will provide practical examples and a step-by-step approach to using congruence proofs effectively in problem-solving scenarios.
Understanding Congruence Proofs
Congruence proofs are based on the principle that if two geometric shapes have the same size and shape, they are congruent. The most common congruence proofs in geometry are:
- Side-Side-Side (SSS)
- Side-Angle-Side (SAS)
- Angle-Side-Angle (ASA)
- Angle-Angle-Side (AAS)
- Hypotenuse-Leg (HL) for right triangles
Step-by-Step Guide to Identifying the Appropriate Proof
- Analyze the given information in the problem.
- Identify the known sides and angles in the geometric figure.
- Determine which congruence theorem aligns with the available information.
- Apply the chosen theorem to prove congruence.
- Use the proven congruence to deduce unknown information.
Practical Examples
Example 1: SSS Congruence
Given: Two triangles ABC and DEF with AB = DE, BC = EF, and AC = DF.
Proof: These triangles are congruent by SSS, as all corresponding sides are equal.
Example 2: SAS Congruence
Given: In triangles PQR and XYZ, PQ = XY, angle P = angle X, and PR = XZ.
Proof: These triangles are congruent by SAS, as two sides and the included angle are equal.
Example 3: ASA Congruence
Given: In triangles LMN and RST, angle L = angle R, LM = RS, and angle N = angle T.
Proof: These triangles are congruent by ASA, as two angles and the included side are equal.
Deducing Unknown Information
Once congruence is established, you can deduce information about unknown angles and sides:
- Corresponding angles in congruent triangles are equal.
- Corresponding sides in congruent triangles are equal.
- If two triangles are congruent, their areas are equal.
Efficiency in Problem-Solving
Using congruence proofs in geometry problems offers several advantages:
- Simplifies complex problems by breaking them into manageable parts.
- Provides a systematic approach to solving geometric puzzles.
- Allows for quick deduction of unknown measurements.
- Enhances logical reasoning and proof-writing skills.
Advanced Application: Overlapping Triangles
In more complex figures with overlapping triangles, congruence proofs can be particularly useful:
- Identify overlapping triangles in the figure.
- Look for shared sides or angles that can help establish congruence.
- Use the proven congruence to deduce information about the larger figure.
Conclusion
Mastering congruence proofs is essential for solving geometry problems. Once you understand the principles and methods, you can apply them to a wide range of geometric scenarios, enhancing your problem-solving skills and mathematical understanding.
Conclusion: Mastering Triangle Congruence
Triangle congruence is a fundamental concept in geometry, stating that two triangles are identical in shape and size. We explored several key methods to prove triangle congruence: Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), and Angle-Angle-Side (AAS). The SSS method requires all three sides of the triangles to be equal, while SAS involves two sides and the included angle. ASA relies on two angles and the included side, and AAS uses two angles and a non-included side. We also discussed the Hypotenuse-Leg (HL) theorem for right triangles. Understanding these proofs is crucial for solving complex geometric problems and constructing logical arguments. By mastering these concepts, students can confidently approach a wide range of triangle-related questions and develop strong spatial reasoning skills. Remember, practice is key to becoming proficient in applying these proofs to various geometric scenarios.
Congruence and Congruent Triangles
Which pairs of triangles are congruent?
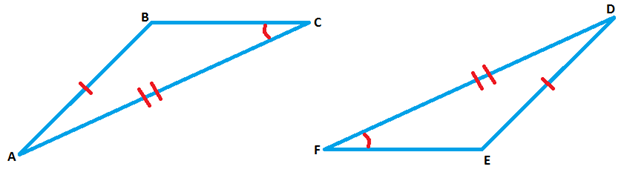
Step 1: Understanding Congruent Triangles
To determine if two triangles are congruent, we need to understand the concept of congruence in geometry. Congruent triangles are triangles that are identical in shape and size. This means that all corresponding angles and sides of the triangles are equal. In other words, if triangle ABC is congruent to triangle DEF, then the following conditions must be met:
- Angle A = Angle D
- Angle B = Angle E
- Angle C = Angle F
- Side AB = Side DE
- Side BC = Side EF
- Side CA = Side FD
Step 2: Identifying Given Information
In the given problem, we are provided with two triangles, and we need to determine if they are congruent. The first step is to identify the information given in the diagram. Look for any marked angles or sides that indicate equality. For instance, if angle C is marked as equal to angle F, this is a piece of information we can use. Similarly, if any sides are marked as equal, note these as well.
Step 3: Analyzing Corresponding Angles and Sides
Next, we need to analyze the corresponding angles and sides of the two triangles. According to the given information:
- Angle C is equal to angle F.
Step 4: Checking for Sufficient Information
To prove that two triangles are congruent, we need sufficient information. This can be achieved through various congruence criteria such as:
- Side-Side-Side (SSS) Congruence: All three sides of one triangle are equal to all three sides of another triangle.
- Side-Angle-Side (SAS) Congruence: Two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle.
- Angle-Side-Angle (ASA) Congruence: Two angles and the included side of one triangle are equal to two angles and the included side of another triangle.
- Angle-Angle-Side (AAS) Congruence: Two angles and a non-included side of one triangle are equal to two angles and a non-included side of another triangle.
Step 5: Conclusion
Based on the given information, we can conclude that there is not enough evidence to determine that the two triangles are congruent. We only know that one pair of angles is equal, which is insufficient to prove congruence. For triangles to be congruent, we need to verify that all corresponding angles and sides are equal, which is not possible with the limited information provided.
FAQs
Here are some frequently asked questions about congruence and congruent triangles:
-
What is the difference between SSS and SAS congruence?
SSS (Side-Side-Side) congruence requires all three sides of two triangles to be equal, while SAS (Side-Angle-Side) congruence requires two sides and the included angle to be equal. SSS is used when you have information about all sides, whereas SAS is used when you have information about two sides and the angle between them.
-
Why is ASA congruence valid but AAA is not?
ASA (Angle-Side-Angle) congruence is valid because it provides enough information to uniquely determine a triangle's shape and size. The side length fixes the scale, while the two angles determine the shape. AAA (Angle-Angle-Angle) only determines the shape but not the size, so it can only prove similarity, not congruence.
-
Can SSA (Side-Side-Angle) be used to prove triangle congruence?
SSA is not generally valid for proving triangle congruence due to the ambiguous case. It can result in two possible triangles, making it unreliable. However, there's an exception: the Hypotenuse-Leg (HL) theorem for right triangles, where SSA can be used if the given angle is the right angle.
-
How does understanding triangle congruence help in real-world applications?
Triangle congruence is crucial in various fields such as engineering, architecture, and surveying. It allows for accurate measurements, structural design, and problem-solving in situations where direct measurements are not possible. For example, in bridge construction, ensuring congruent support structures is essential for stability and load distribution.
-
What is the CPCTC principle, and how does it relate to triangle congruence?
CPCTC stands for "Corresponding Parts of Congruent Triangles are Congruent." This principle states that if two triangles are proven congruent, then all their corresponding parts (sides and angles) are also congruent. It's a powerful tool in geometry proofs, allowing us to deduce additional information about triangles once congruence is established.
Prerequisite Topics for Congruence and Congruent Triangles
Understanding congruence and congruent triangles is a fundamental concept in geometry, but to fully grasp this topic, it's crucial to have a solid foundation in several prerequisite areas. These building blocks not only enhance your comprehension but also provide the necessary tools to solve more complex problems involving congruent triangles.
One essential prerequisite is the hypotenuse-leg theorem for right triangles. This theorem, which is closely related to the sine ratio, helps in understanding the relationships between sides and angles in right triangles. Mastering this concept is crucial because congruent triangles often involve comparing corresponding sides and angles, and the ability to calculate these elements accurately is paramount.
Another important foundation is understanding distance and time questions in linear equations. While this may seem unrelated at first glance, it actually plays a significant role in developing problem-solving skills and logical thinking, which are essential when proving triangle congruence. The ability to manipulate equations and understand relationships between variables directly translates to working with triangle properties and congruence proofs.
The concept of using sine ratios to calculate angles and sides is another critical prerequisite. This trigonometric principle is fundamental in analyzing triangles, especially when dealing with right triangles. Understanding sine ratios provides a powerful tool for comparing triangle properties, which is at the heart of proving congruence.
Lastly, familiarity with proving triangles congruent by ASA and AAS is a direct precursor to more advanced congruence concepts. These proofs introduce the logical steps and reasoning required to establish congruence between triangles. Mastering ASA (Angle-Side-Angle) and AAS (Angle-Angle-Side) proofs builds a strong foundation for understanding more complex congruence scenarios.
By solidifying your understanding of these prerequisite topics, you'll be well-equipped to tackle the intricacies of congruence and congruent triangles. Each of these concepts contributes to a comprehensive understanding of triangle properties, measurement, and proof techniques. As you progress in your study of geometry, you'll find that these foundational skills continually resurface, reinforcing their importance in mastering more advanced geometric concepts.
Remember, mathematics is a subject built on interconnected ideas. Taking the time to thoroughly understand these prerequisites will not only make learning about congruence and congruent triangles easier but will also enhance your overall mathematical prowess. As you delve into the world of congruent triangles, you'll appreciate how these foundational concepts come together to form a cohesive and powerful set of geometric tools.

