Adding with regrouping
Topic Notes
In this lesson, we will learn:
- How to use base ten materials to represent numbers
- Writing numbers in expanded form
Notes:
- Regrouping
10 ones can be regrouped into 1 ten:
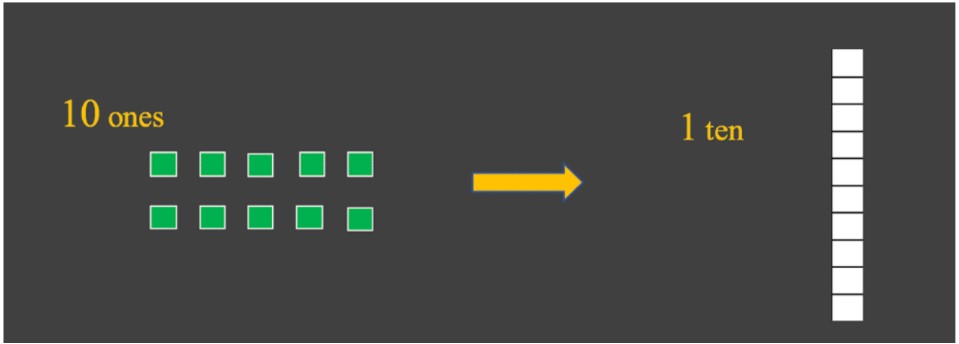
10 tens can be regrouped into 1 hundred:
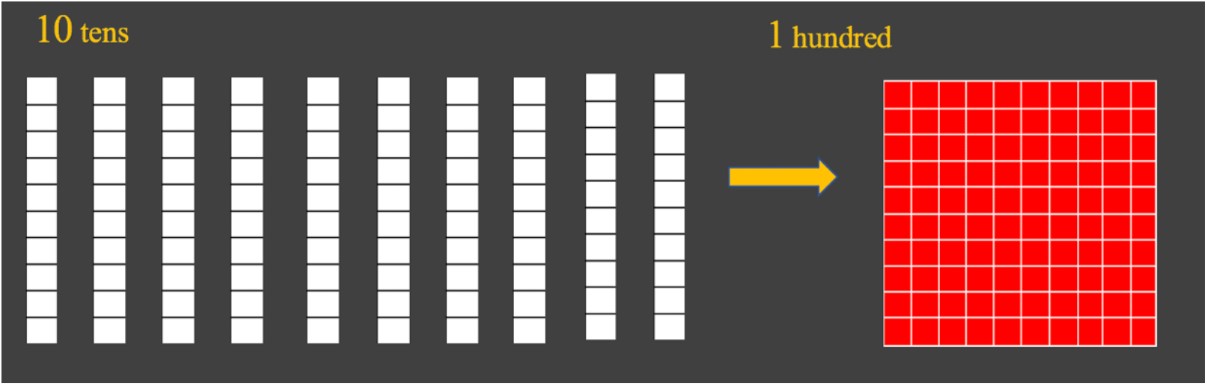
10 hundreds can be regrouped into 1 thousand
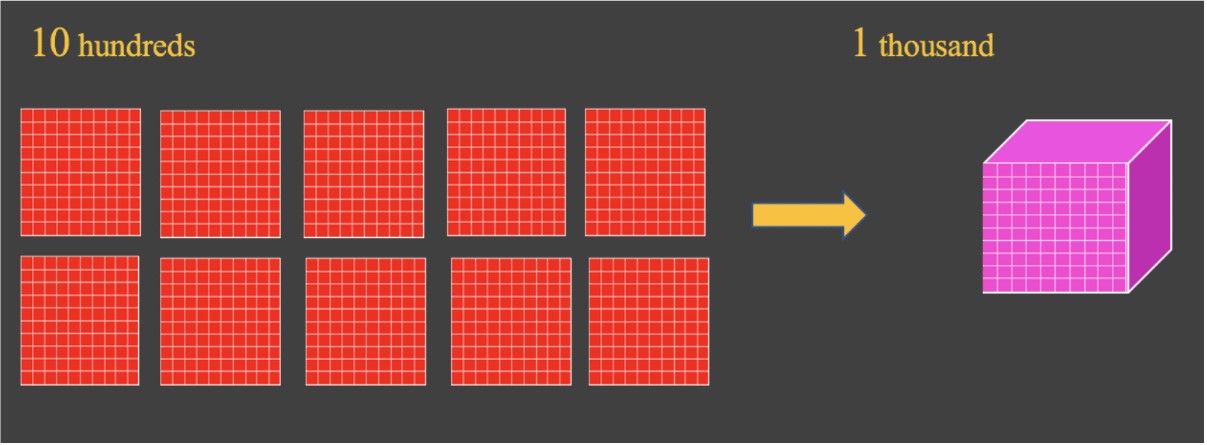
Introduction to Base 10 Blocks
Base 10 blocks are essential tools in the math classroom, helping students grasp the fundamental concept of numbers and place value. These manipulatives consist of units, rods, flats, and cubes, representing ones, tens, hundreds, and thousands respectively. By using these tangible objects, learners can visualize abstract numerical concepts, making it easier to understand addition, subtraction, and place value. Our introduction video serves as a crucial starting point, demonstrating how to use base 10 blocks effectively. It guides students through hands-on activities, allowing them to see and feel the relationships between different number values. This visual and tactile approach is particularly beneficial for kinesthetic learners and those who struggle with abstract mathematical concepts. As students progress, they can use base 10 blocks to explore more complex operations, building a solid foundation for future mathematical learning. Incorporating these blocks into lessons enhances engagement and promotes a deeper understanding of numerical relationships.
Understanding Base 10 Blocks
Base 10 blocks are a fantastic hands-on tool used in math education to help students visualize and understand place value in our decimal number system. These colorful, physical manipulatives come in four different sizes, each representing a specific place value: ones, tens, hundreds, and thousands. Let's dive into each type of block and explore how they work together to make math concepts more tangible and easier to grasp.
Ones Block
The smallest unit in the base 10 block system is the ones block. Imagine a tiny cube that fits perfectly in the palm of your hand. This little cube represents a single unit or the number 1. It's usually about 1 centimeter on each side, making it easy for young hands to manipulate. When you're counting or adding single digits, these are the blocks you'll use most often. For example, if you want to show the number 5, you'd line up five of these small cubes in a row.
Tens Block
Next up is the tens block. Picture a long, rectangular prism that's made up of 10 ones blocks stuck together. It's like a row of 10 tiny cubes fused into one piece. This block represents the number 10 and is crucial for helping students understand grouping and the concept of place value. When you're working with numbers between 10 and 99, you'll use a combination of tens blocks and ones blocks. For instance, the number 23 would be shown with two tens blocks and three ones blocks.
Hundreds Block
The hundreds block takes things up a notch. Imagine a flat square that's 10 ones blocks wide and 10 ones blocks long. This creates a 10x10 grid, giving you 100 tiny cubes in total. This single flat square represents the number 100. It's a powerful visual aid for demonstrating how 10 tens make a hundred. When working with numbers from 100 to 999, you'll use a mix of hundreds, tens, and ones blocks. For example, 352 would be shown with three hundreds blocks, five tens blocks, and two ones blocks.
Thousands Block
The largest of the base 10 blocks is the thousands block. Picture a big cube made up of 10 hundreds blocks stacked on top of each other. This impressive block represents 1,000 and really helps students grasp the magnitude of larger numbers. It's like having 10x10x10 ones blocks all in one solid cube. When dealing with four-digit numbers, you'll incorporate the thousands block along with the other sizes. For instance, 2,586 would be represented by two thousands blocks, five hundreds blocks, eight tens blocks, and six ones blocks.
Why Base 10 Blocks are Essential in Math Education
Base 10 blocks are invaluable in math education for several reasons. Firstly, they provide a concrete, visual representation of abstract numerical concepts. This hands-on approach helps students build a strong foundation in place value, which is crucial for understanding more complex math operations later on. The blocks also make it easier for students to see the relationships between different place values, like how 10 ones make a ten, or 10 tens make a hundred.
Moreover, these blocks are excellent for teaching addition, subtraction, multiplication, and even division. Students can physically manipulate the blocks to solve problems, which reinforces their understanding of these operations. For example, when adding 23 and 45, students can combine two tens blocks with three ones blocks, then add four tens blocks and five ones blocks. They can then see how to regroup 10 ones into a new tens block, arriving at the correct answer of 68.
Base 10 blocks also help in developing number sense and estimation skills. By working with these physical representations, students gain a better intuition for the relative sizes of numbers and can more easily estimate sums, differences, and products. This tactile experience creates lasting mental images that students can draw upon even when they're no longer using the physical blocks.
In conclusion, base 10 blocks are a powerful tool in math education, bridging the gap between concrete and abstract thinking. By providing a visual and tactile
Representing Numbers with Base 10 Blocks
Base 10 blocks are an excellent tool for visualizing and understanding numbers, especially when it comes to place value. These blocks come in four sizes: units (small cubes), rods (representing tens), flats (representing hundreds), and large cubes (representing thousands). Let's explore how to use these blocks to represent numbers and reinforce place value concepts.
Step-by-Step Instructions:
- Identify the number you want to represent.
- Break the number down into its place values (ones, tens, hundreds, thousands).
- Select the appropriate blocks for each place value.
- Arrange the blocks to visually represent the number.
Example: Representing 346
Let's walk through representing the number 346 using base 10 blocks:
- 3 hundreds: Use 3 flat blocks
- 4 tens: Use 4 rod blocks
- 6 ones: Use 6 unit blocks
Arrange these blocks together to visually show 346.
Relationship to Place Value
Base 10 blocks directly correspond to our place value system:
- Unit cubes = ones place
- Rods = tens place
- Flats = hundreds place
- Large cubes = thousands place
This physical representation helps students understand that each place value is ten times greater than the one to its right.
Practice Exercises
Try representing these numbers using base 10 blocks:
- 124
- 508
- 2,375
Additional Tips
- Always start with the largest place value when building your number.
- Practice regrouping by exchanging 10 of one block type for 1 of the next larger block.
- Use base 10 blocks to visualize addition and subtraction operations.
Representing numbers with base 10 blocks is a hands-on way to reinforce place value understanding. It allows students to physically manipulate numbers, making abstract concepts more concrete. As you practice, you'll find that this method enhances your ability to work with larger numbers and perform mental math operations. Remember, the key is to connect the physical representation with the numerical concept, building a strong foundation for more advanced mathematical skills.
Regrouping with Base 10 Blocks
Regrouping is a fundamental concept in mathematics that plays a crucial role in addition and subtraction. It's a process where we exchange units of one place value for an equivalent amount in another place value. To understand this better, let's explore regrouping using base 10 blocks.
Base 10 blocks are visual aids that represent different place values: ones (small cubes), tens (rods), hundreds (flats), and thousands (large cubes). These blocks help us see how numbers are composed and how regrouping works in practice.
Why is regrouping important? It allows us to perform calculations that involve carrying over or borrowing, which is essential for solving more complex addition and subtraction problems. Let's look at some examples:
Regrouping Hundreds as Thousands
Imagine we're adding 854 + 372. When we add the hundreds column (8 + 3), we get 11 hundreds. However, we can't write 11 in the hundreds place. Instead, we regroup 10 of those hundreds as 1 thousand, leaving 1 hundred. Visually, we'd exchange 10 hundred flats for 1 thousand cube.
Regrouping Tens as Hundreds
In the same problem, adding the tens (5 + 7) gives us 12 tens. We regroup 10 of these tens as 1 hundred, leaving 2 tens. With base 10 blocks, we'd exchange 10 ten rods for 1 hundred flat.
Regrouping Ones as Tens
Finally, adding the ones (4 + 2) results in 6 ones, which doesn't require regrouping. However, in a problem like 38 + 45, adding 8 and 5 gives us 13 ones. We'd regroup 10 of these ones as 1 ten, exchanging 10 unit cubes for 1 ten rod.
Now, let's walk through a step-by-step example of regrouping in subtraction:
Subtracting with Regrouping: 734 - 256
- Start with 734 represented by base 10 blocks: 7 hundred flats, 3 ten rods, and 4 unit cubes.
- We can't subtract 6 ones from 4 ones, so we need to regroup. Take 1 ten rod and exchange it for 10 unit cubes.
- Now we have 7 hundred flats, 2 ten rods, and 14 unit cubes.
- Subtract 6 ones from 14 ones, leaving 8 ones.
- Move to the tens place. We can subtract 5 tens from 2 tens, so we need to regroup again. Take 1 hundred flat and exchange it for 10 ten rods.
- Now we have 6 hundred flats, 12 ten rods, and 8 unit cubes.
- Subtract 5 tens from 12 tens, leaving 7 tens.
- Finally, subtract 2 hundreds from 6 hundreds, leaving 4 hundreds.
- Our final answer is 478.
Remember, regrouping might seem tricky at first, but with practice, it becomes second nature. Don't be discouraged if it takes time to master every math whiz started where you are now! Use base 10 blocks or draw pictures to help visualize the process. As you work through problems, think about what each number represents in terms of hundreds, tens, and ones.
Regrouping is like reorganizing your toy box. Sometimes you need to move things around to make everything fit just right. With addition, you're putting more toys in the box and might need to create a new group. With subtraction, you're
Expanded Form and Base 10 Blocks
Base 10 blocks are fantastic tools that help us understand how numbers are built, and they're closely related to writing numbers in expanded form. Let's explore this connection and see how it ties into place value!
When we use base 10 blocks, we represent numbers using different sized pieces. The smallest cube represents one, a bar represents ten, a flat represents a hundred, and a large cube represents a thousand. This visual representation directly relates to expanded form, where we break down a number into the sum of its place values.
For example, let's take the number 831. In base 10 blocks, we'd use 8 flats (hundreds), 3 bars (tens), and 1 cube (ones). Now, to write 831 in expanded form, we do the same thing, but with numbers: 800 + 30 + 1. See the connection? Each part of the expanded form corresponds to a type of base 10 block!
This is where place value comes in. In 831, the 8 is in the hundreds place, the 3 is in the tens place, and the 1 is in the ones place. Expanded form simply takes each digit and multiplies it by its place value: 8 x 100, 3 x 10, and 1 x 1.
Let's try another example: 2,547. In expanded form, this becomes 2,000 + 500 + 40 + 7. With base 10 blocks, we'd use 2 large cubes, 5 flats, 4 bars, and 7 small cubes. The expanded form matches exactly how we'd build the number with blocks!
Now, it's your turn to practice! Try writing these numbers in expanded form:
- 456
- 1,209
- 3,075
Remember, break each number down by its place value. For 456, think about how many hundreds, tens, and ones you'd need in base 10 blocks.
Don't worry if it seems tricky at first with practice, you'll get better! Expanded form is a powerful way to understand the structure of numbers, and it's a skill that will help you in many areas of math.
Here's a tip: When you're stuck, try drawing the base 10 blocks for the number. Then, write down what each block represents in numbers. Before you know it, you'll have the expanded form!
Keep practicing, and soon you'll be a pro at expanded form and place value. Remember, every large number is just a combination of smaller parts just like building with blocks. You've got this!
Practical Applications of Base 10 Blocks
Base 10 blocks are not just classroom tools; they have real-world applications that make math come alive in our everyday experiences. These versatile manipulatives help us visualize and solve problems in various practical scenarios, from handling money to converting measurements. Let's explore how these blocks bridge the gap between abstract math concepts and tangible real-life situations.
One of the most common real-world applications of base 10 blocks is in money calculations. Imagine you're planning a budget for a home renovation project. You can use unit cubes to represent pennies, rods for dimes, flats for dollar bills, and large cubes for hundred-dollar bills. This visual representation makes it easier to add up expenses, calculate change, or determine how much more you need to save for your project goals.
Let's try an interactive scenario: You have $245 saved for your renovation, represented by two large cubes (hundreds), four rods (tens), and five unit cubes (ones). If a new paint job costs $180, how much will you have left? Using the blocks, you can physically remove one large cube and eight rods, leaving you with six rods and five unit cubes or $65. This hands-on approach makes the subtraction process more intuitive and less prone to errors.
Another practical use of base 10 blocks is in measurement conversions. When dealing with metric units, these blocks can represent different scales effortlessly. A unit cube could symbolize one milliliter, a rod 10 milliliters, a flat 100 milliliters, and a large cube one liter. This visual aid is particularly helpful when converting between units or solving problems involving capacity.
Consider this scenario: You're following a recipe that calls for 750 milliliters of water, but your measuring cup only shows liters. With base 10 blocks, you can quickly visualize that 750 milliliters is equivalent to seven flats and five rods, or three-quarters of a large cube (liter). This mental image helps you accurately measure the required amount without the need for complex calculations.
Base 10 blocks also shine in real-world problem-solving involving area and volume calculations. In landscaping, for instance, you might need to calculate how much mulch is needed to cover a garden bed. By using flats to represent square meters and large cubes for cubic meters, you can easily model the space and determine the volume of mulch required. This visual approach makes it simpler to estimate materials and costs for various home improvement projects.
Let's engage in one more interactive example: You're tiling a kitchen backsplash that measures 2 meters by 0.5 meters. Using base 10 blocks, with each flat representing one square meter, how would you model this area? You'd need one full flat and half of another, visually showing that the total area is 1 square meter. If each tile covers 0.1 square meters (represented by a rod), how many tiles would you need? You can see that 10 rods fit into one flat, so you'd need 10 tiles for the full square meter.
The beauty of base 10 blocks in these real-world applications is their ability to make abstract concepts concrete. They provide a tactile and visual way to approach problems that might otherwise seem daunting. Whether you're balancing a checkbook, converting recipes, or planning home improvements, thinking in terms of these blocks can simplify your calculations and improve your mathematical intuition.
As you go about your day, challenge yourself to spot opportunities where base 10 blocks could be applied. From calculating tips at restaurants to estimating the paint needed for a room, these mental models can enhance your problem-solving skills and make math more accessible and enjoyable in everyday life. Remember, math isn't just about numbers on a page it's a powerful tool for understanding and navigating the world around us, and base 10 blocks are your key to unlocking that potential.
Conclusion
Base 10 blocks are essential tools for understanding numbers, regrouping, and expanded form. These manipulatives provide a tangible representation of place value, making abstract mathematical concepts more concrete. The introduction video effectively visualizes these ideas, helping learners grasp the fundamental principles of our number system. By practicing with physical or virtual base 10 blocks, students can reinforce their understanding of place value and develop a strong foundation for more advanced mathematical concepts. This hands-on approach enhances number sense and problem-solving skills, crucial for success in mathematics. We encourage readers to explore further resources on understanding numbers and continue engaging with these concepts. Whether you're a student, teacher, or parent, incorporating base 10 blocks into your learning or teaching strategy can significantly improve mathematical comprehension. Take the next step in your mathematical journey by experimenting with base 10 blocks and discovering their transformative power in understanding numbers.
Example:
Representing Numbers with Blocks
Show these numbers using base ten blocks: 28
Step 1: Understanding the Number 28
To represent the number 28 using base ten blocks, we first need to understand the number itself. The number 28 is composed of two digits: 2 and 8. Each digit has a specific place value. The digit 2 is in the tens place, and the digit 8 is in the ones place. Understanding place value is crucial because it tells us how many tens and ones blocks we need to use.
Step 2: Identifying the Tens Place
Next, we focus on the tens place. In the number 28, the digit 2 is in the tens place. This means we need to use tens blocks to represent this part of the number. Each tens block represents ten units. Therefore, for the digit 2 in the tens place, we need 2 tens blocks. This is because 2 tens blocks equal 20 (2 x 10 = 20).
Step 3: Identifying the Ones Place
Now, we look at the ones place. In the number 28, the digit 8 is in the ones place. This means we need to use ones blocks to represent this part of the number. Each ones block represents one unit. Therefore, for the digit 8 in the ones place, we need 8 ones blocks. This is because 8 ones blocks equal 8 (8 x 1 = 8).
Step 4: Combining the Blocks
After identifying the number of tens and ones blocks needed, we combine them to represent the number 28. We have 2 tens blocks and 8 ones blocks. When we put these blocks together, we get the complete representation of the number 28 using base ten blocks. The 2 tens blocks represent 20, and the 8 ones blocks represent 8. Together, they sum up to 28 (20 + 8 = 28).
Step 5: Visual Representation
To visualize this, imagine two long blocks (each representing ten units) and eight small blocks (each representing one unit). Arrange the two long blocks side by side, and then place the eight small blocks next to them. This visual arrangement helps in understanding how the number 28 is constructed using base ten blocks.
Step 6: Verification
Finally, we verify our representation. We have 2 tens blocks, which equal 20, and 8 ones blocks, which equal 8. Adding these together gives us 28. This confirms that our representation using base ten blocks is accurate. Understanding and verifying this process ensures that we can correctly represent any number using base ten blocks in the future.
FAQs
-
What are base 10 blocks and how do they help in learning mathematics?
Base 10 blocks are manipulative tools used in mathematics education to represent numbers visually. They consist of units (small cubes), rods (tens), flats (hundreds), and large cubes (thousands). These blocks help students understand place value, addition, subtraction, and other mathematical concepts by providing a tangible representation of numbers.
-
How do base 10 blocks relate to place value?
Base 10 blocks directly correspond to our place value system. Each block size represents a different place value: unit cubes for ones, rods for tens, flats for hundreds, and large cubes for thousands. This physical representation helps students visualize that each place value is ten times greater than the one to its right, reinforcing the concept of place value in our decimal system.
-
Can base 10 blocks be used for addition and subtraction?
Yes, base 10 blocks are excellent for teaching addition and subtraction. Students can physically combine or remove blocks to perform these operations, making the process more concrete. For example, when adding 23 and 45, students can combine two tens rods with three unit cubes, then add four tens rods and five unit cubes. This visual method helps in understanding regrouping and carrying over in addition and subtraction.
-
How do base 10 blocks help in understanding expanded form?
Base 10 blocks directly relate to expanded form by visually representing each place value. For instance, the number 234 would be represented by 2 flats (hundreds), 3 rods (tens), and 4 unit cubes (ones). This corresponds to the expanded form 200 + 30 + 4. The blocks make it easy to see how a number is composed of different place values, which is the essence of expanded form.
-
Are there any real-world applications for the concepts learned with base 10 blocks?
Absolutely! The concepts learned with base 10 blocks have numerous real-world applications. They help in understanding money calculations, measurement conversions, and even area and volume calculations. For example, in budgeting, unit cubes can represent pennies, rods for dimes, flats for dollar bills, and large cubes for hundred-dollar bills. This makes financial calculations more intuitive and relatable to everyday experiences.
Prerequisite Topics for Base Ten Blocks and Numbers
Understanding base ten blocks and numbers is a fundamental concept in mathematics that builds upon several key prerequisite topics. One of the most crucial foundations is understanding place value. This concept is essential because base ten blocks visually represent the place value system, helping students grasp how numbers are structured in our decimal system.
Another important prerequisite is addition and subtraction with regrouping. When working with base ten blocks, students often need to exchange blocks of different values, which directly relates to regrouping in arithmetic operations. This skill is vital for manipulating numbers effectively using the base ten system.
The decimal number system forms the core of base ten blocks. Understanding how this system works is crucial for students to make sense of the blocks' representation of numbers. It provides the context for why we use tens, hundreds, and thousands in our number system.
Understanding number systems in general is also vital. While base ten is our primary system, knowing about other number systems can help students appreciate the logic behind base ten and how it compares to alternatives. This broader perspective enhances their grasp of numerical concepts.
The expanded form of numbers is closely related to base ten blocks. Each block represents a specific place value, which directly corresponds to how numbers are written in expanded form. This connection helps students visualize the composition of multi-digit numbers.
Lastly, understanding numerical relationships is crucial when working with base ten blocks. The blocks provide a concrete way to explore relationships between numbers, such as comparing magnitudes or visualizing multiplication as repeated addition.
By mastering these prerequisite topics, students build a strong foundation for working with base ten blocks and numbers. This understanding not only aids in immediate mathematical tasks but also lays the groundwork for more advanced concepts in algebra and beyond. The visual and tactile nature of base ten blocks serves as a bridge between abstract numerical concepts and concrete representations, making mathematics more accessible and engaging for learners of all levels.

