What are variables in algebra?
Topic Notes
In this lesson, we will learn:
- The parts of a math equation for all four operations: addition, subtraction, multiplication, division
- How to do basic algebra: solving for unknowns (variables) in equations
- How to write algebra equations from word sentences by using equation models to help
Notes:
- A math equation can be thought of as a mathematical sentence which needs terms, an operation and an answer

- An unknown is a value that we don't know in an equation yet; we need to solve the equation to find the unknown through guess-and-check (knowing that values must be equal on both sides of the equal sign)
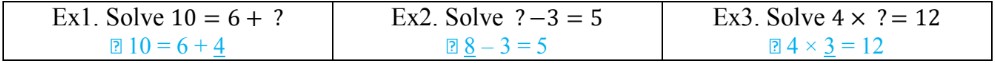
- Algebra is a type of math where we will see BOTH numbers and letters (or symbols)!
- We use variables (letters or symbols) to represent unknown values:
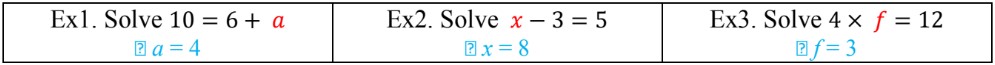
- Equation models help identify all the terms when you're dealing with word sentences so that you can write an algebra equation

- i.e. "36 added to 41 equals ." →36 + 41 =
- i.e. "15 less than equals 13." → - 15 = 13
- i.e. "2 times as many as 7 is ." →2 × 7 =
- i.e. " is 3 times less than 15" → = 15 ÷ 13
- Keywords (key phrases) for each operation include:
- Addition: "added to", "more than", "increased by"
- Subtraction: "subtracted from", "less than", "decreased by"
- Multiplication: "multiplied by", "times", "times as many", "each", "groups"
- Division: "divided by", "times as many", "split into groups"
Introduction: What are Variables in Algebra?
Welcome to the fascinating world of algebra! At the heart of this mathematical realm lies a powerful concept: variables. These are symbols, usually letters like x or y, that represent unknown quantities in equations. Variables are the building blocks of algebraic expressions and equations, allowing us to solve complex problems and model real-world situations. Our introduction video provides a clear, visual explanation of variables, making it an essential starting point for your algebra journey. As you watch, you'll discover how variables can represent different values and how they're used in equations. This understanding is crucial for mastering more advanced algebraic concepts. Whether you're just beginning or looking to refresh your knowledge, grasping the concept of variables is your first step towards becoming an algebra expert. So, let's dive in and explore the exciting world of variables together!
Understanding Math Equations
Math equations are like mathematical sentences that express relationships between numbers and variables. They are fundamental to understanding and solving problems in mathematics and various real-world applications. At their core, math equations consist of three main components: terms, operations, and answers.
Components of Math Equations
1. Terms: These are the individual numbers or variables in an equation. For example, in the equation 3 + 5 = 8, the terms are 3, 5, and 8.
2. Operations: These are the mathematical actions performed on the terms. Common operations include addition (+), subtraction (-), multiplication (×), and division (÷).
3. Answer: This is the result of the operation(s) performed on the terms. In an equation, the answer is typically found on one side of the equal sign (=).
Types of Math Equations
Let's explore different types of math equations using the four basic operations:
Addition Equations
Addition equations involve combining two or more terms to find their sum. For example:
- 2 + 3 = 5
- 10 + 15 + 20 = 45
Subtraction Equations
Subtraction equations involve finding the difference between two terms. For instance:
- 8 - 3 = 5
- 20 - 7 = 13
Multiplication Equations
Multiplication equations involve repeated addition or finding the product of two or more terms. Examples include:
- 4 × 3 = 12
- 5 × 6 × 2 = 60
Division Equations
Division equations involve splitting a quantity into equal parts or finding how many times one number goes into another. For example:
- 12 ÷ 3 = 4
- 20 ÷ 5 = 4
Understanding these basic types of division equations is crucial for building a strong foundation in mathematics. As students progress, they encounter more complex equations that combine multiple operations and include variables. These advanced equations are used to solve real-world problems in fields such as physics, engineering, and economics.
To solve math equations effectively, it's important to follow the order of operations PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction). This ensures that the operations are performed in the correct sequence, leading to accurate results.
Practicing with various types of math equations helps develop problem-solving skills and mathematical thinking. As you work with equations, remember that they are tools for expressing relationships and finding solutions. By breaking down complex problems into simpler equations, you can tackle even the most challenging mathematical concepts.
Introducing Unknowns in Equations
In mathematics, unknowns are variables in equations that represent values we need to find. These unknowns are typically represented by letters like x, y, or z. Solving simple equations with unknowns is a fundamental skill in algebra and beyond. One method to solve for these unknowns is the guess-and-check method, which can be particularly useful when dealing with simple equations or when other algebraic methods seem complex.
The guess-and-check method, also known as trial and error, involves making educated guesses about the value of the unknown and then checking if that guess satisfies the equation. This method can be an excellent starting point for students learning to solve equations, as it helps develop intuition about how equations work.
Let's illustrate this concept using the grape equation model. Imagine you have a bowl of grapes, and you know that the total number of grapes is 24. You also know that the grapes are divided equally among 4 small plates. We can represent this scenario with the equation: 4x = 24, where x is the unknown number of grapes on each plate.
To solve this using the guess-and-check method:
- Make an initial guess: Let's guess x = 5
- Check the guess: 4 × 5 = 20 (This is close but not equal to 24)
- Adjust the guess: Since 20 is less than 24, we need to increase our guess
- Try again: Let's guess x = 6
- Check again: 4 × 6 = 24 (This satisfies the equation)
Through this process, we've determined that x = 6, meaning there are 6 grapes on each plate.
While the guess-and-check method is straightforward, it's important to note that it may not always be the most efficient method, especially for more complex equations. However, it serves as an excellent introduction to solving simple equations and can help students build confidence in their problem-solving abilities.
As students progress, they can learn more advanced techniques for solving equations, such as:
- Isolating the variable
- Using inverse operations
- Balancing equations
- Factoring
- Using the quadratic formula for quadratic equations
Understanding how to solve for unknowns is crucial in many real-world applications of equations. Engineers use equations to design structures, economists use them to model financial systems, and scientists use them to describe natural phenomena. By mastering the skill of solving for unknowns, students open doors to a wide range of academic and professional opportunities.
In conclusion, unknowns in equations represent values we need to determine to solve a problem. The guess-and-check method is a simple yet effective way to solve for these unknowns, especially when beginning to learn algebra. As illustrated by the grape equation model, this method involves making educated guesses and verifying them against the equation. While more advanced methods exist, the guess-and-check approach provides a solid foundation for understanding how equations work and how to approach solving them systematically.
Variables in Algebra
Variables are fundamental components in algebra that represent unknown values in equations. These symbols, typically letters from the alphabet, allow mathematicians and students to work with quantities that may vary or are yet to be determined. Understanding variables is crucial for solving equations with variables, expressing relationships between quantities, and modeling real-world scenarios mathematically.
In algebra, variables serve as placeholders for numbers. They can represent a specific unknown value that needs to be solved for, or they can represent a range of possible values in a given context. The most commonly used variables are letters such as x, y, and z, but any letter or symbol can be used as long as its meaning is clearly defined within the problem.
For example, in the equation 2x + 5 = 13, x is a variable representing the unknown value that, when multiplied by 2 and added to 5, equals 13. In this case, x has a specific value (4) that satisfies the equation. However, in an expression like y = 3z + 2, both y and z are variables that can take on different values, with y depending on the value of z.
Variables are not limited to single letters. They can also be represented by words or phrases, especially in applied problems. For instance, in a physics equation, "v" might represent velocity, "t" for time, or "d" for distance. This use of meaningful variable names helps in understanding the context of the problem more easily.
The power of variables lies in their ability to generalize mathematical relationships. They allow us to express relationships with variables and formulas that hold true for many different numerical values. For example, the area of a rectangle can be expressed as A = l × w, where A represents the area, l the length, and w the width. This formula works for any rectangle, regardless of its specific dimensions.
In more advanced algebra, variables can represent not just numbers but also functions, vectors, or even abstract mathematical objects. This versatility makes variables an essential tool in all branches of mathematics and its applications in science, engineering, and economics.
When working with variables, it's important to remember that they can represent different types of numbers depending on the context. They might represent integers, rational numbers, real numbers, or even complex numbers. The domain of a variable (the set of values it can take) is often specified or implied by the problem at hand.
Variables also play a crucial role in graphing. In coordinate geometry, x and y variables are used to represent points on a plane. Functions are often expressed in terms of variables, such as f(x) = x² + 2x + 1, where x is the independent variable and f(x) is the dependent variable.
Understanding how to manipulate and solve for variables is a key skill in algebra. This involves techniques such as isolating variables, substituting known values, and using algebraic operations to simplify expressions containing variables. These skills form the foundation for more advanced mathematical concepts and problem-solving strategies.
In conclusion, variables are the building blocks of algebraic thinking. They allow us to express general relationships, solve for unknown values in equations, and model complex systems. By mastering the use of variables, students gain a powerful tool for mathematical reasoning and problem-solving that extends far beyond the classroom into various fields of study and real-world applications.
Writing Algebra Equations from Word Sentences
Equation models are powerful tools that help bridge the gap between word problems and algebraic expressions. These visual representations serve as a crucial step in translating word problems into mathematical equations. By using equation models, students can more easily identify the key terms and relationships within word sentences, making it simpler to convert them into algebra equations.
Equation models typically consist of boxes or circles connected by operation symbols, representing the unknown values in equations and the relationships between them. These models are particularly useful for all four basic operations: addition, subtraction, multiplication, and division. Let's explore how equation models help in converting word sentences to algebra equations for each operation.
Addition Equation Model
For addition problems, the equation model usually shows two or more boxes connected by plus signs, leading to a result box. For example, consider the word sentence: "The sum of a number and 7 is 15." Using an equation model, we can represent this as:
(?) + (7) = (15)
This visual representation helps us identify the unknown number, leading to the algebraic equation: x + 7 = 15
Subtraction Equation Model
Subtraction models typically show a larger box with a smaller box being taken away, resulting in a difference box. For instance, the sentence "A number decreased by 5 equals 10" can be modeled as:
(?) - (5) = (10)
This model clearly illustrates the subtraction operation, leading to the equation: x - 5 = 10
Multiplication Equation Model
Multiplication models often use repeated addition or arrays to represent the operation. For the sentence "Three times a number is equal to 24," we can use a model like:
(?) × (3) = (24)
This representation helps students visualize the multiplication, resulting in the equation: 3x = 24
Division Equation Model
Division models typically show a larger quantity being split into equal groups. For example, "A number divided by 4 is 6" can be modeled as:
(?) ÷ (4) = (6)
This model clearly illustrates the division operation, leading to the equation: x ÷ 4 = 6 or x/4 = 6
By using these equation models, students can more easily identify the key components of word problems: 1. The unknown values in equations (often represented by a variable like x) 2. The given values (specific numbers in the problem) 3. The operation(s) being performed 4. The relationship between the values (equality or inequality)
Equation models also help in more complex scenarios involving multiple operations. For instance, consider the word sentence: "Twice the sum of a number and 3 is equal to 18." We can break this down using a combination of models:
((?) + (3)) × (2) = (18)
This visual representation clearly shows the order of operations and helps translate the sentence into the algebraic equation: 2(x + 3) = 18
As students become more comfortable with equation models, they develop a stronger intuition for translating word problems into algebraic expressions. This skill is crucial for solving real-world problems and advancing in mathematics. Equation models serve as a bridge between concrete, visual representations and abstract algebraic thinking.
To effectively use equation models, students should: 1. Carefully read the word problem and identify key terms indicating operations 2. Determine the unknown value(s) and represent them with variables 3. Use boxes or circles to represent known and unknown values
Keywords for Mathematical Operations
Understanding keywords associated with mathematical operations is crucial for solving word problems. Let's explore the common terms used for addition, subtraction, multiplication, and division.
Addition Keywords
Addition is often indicated by words like "sum," "total," "plus," "increase," "more than," and "combined." For example, "What is the sum of 5 and 7?" or "If John has 3 apples and Mary gives him 2 more, how many apples does John have in total?"
Subtraction Keywords
Subtraction is typically signaled by terms such as "difference," "minus," "less than," "decrease," "reduce," and "take away." A word problem might ask, "What is the difference between 10 and 6?" or "If Sarah had 8 cookies and ate 3, how many cookies does she have left?"
Multiplication Keywords
Multiplication often uses words like "product," "times," "multiplied by," "of," and "groups of." An example problem could be, "What is the product of 4 and 5?" or "If there are 3 rows of chairs with 4 chairs in each row, how many chairs are there in total?"
Division Keywords
Division is frequently indicated by phrases such as "quotient," "divided by," "per," "out of," and "split equally." A division word problem might ask, "What is 12 divided by 3?" or "If 15 candies are shared equally among 5 children, how many candies does each child receive?"
Applying Keywords in Word Problems
When solving word problems, it's essential to identify these keywords to determine which operation to use. For instance, "Jenny has 5 marbles. Tom gives her 3 more. How many marbles does Jenny have now?" The phrase "gives her 3 more" indicates addition. Similarly, "A bakery sold 48 cupcakes. If they were packaged in boxes of 6, how many boxes were used?" The phrase "packaged in boxes of 6" suggests division.
It's important to note that some problems may use less obvious language or combine multiple operations. For example, "A store has 4 shelves, each holding 6 books. If they sell 5 books, how many remain?" This problem requires both multiplication (4 x 6) and subtraction (24 - 5).
By familiarizing yourself with these keywords and practicing their application in various contexts, you'll become more proficient at interpreting and solving mathematical word problems. Remember, context is key, and sometimes the same word can indicate different operations depending on how it's used in the problem.
Practice: Converting Word Sentences to Algebra Equations
Converting word sentences to algebra equations is a crucial skill in mathematics. This process involves translating everyday language into mathematical expressions, using variables, numbers, and operations. Let's explore several examples to guide you through this conversion process.
Example 1: "A number plus 5 equals 12"
Step 1: Identify the unknown number. Let's call it x.
Step 2: Translate "plus 5" into mathematical notation: x + 5
Step 3: "equals 12" becomes the right side of the equation.
Final equation: x + 5 = 12
Example 2: "Twice a number decreased by 3 is 15"
Step 1: Let the unknown number be y.
Step 2: "Twice a number" translates to 2y.
Step 3: "decreased by 3" means we subtract 3: 2y - 3
Step 4: "is 15" forms the right side of the equation.
Final equation: 2y - 3 = 15
Example 3: "The sum of three consecutive integers is 42"
Step 1: Let the first integer be n.
Step 2: The next two integers will be n + 1 and n + 2.
Step 3: Sum these three: n + (n + 1) + (n + 2)
Step 4: Set this equal to 42.
Final equation: n + (n + 1) + (n + 2) = 42
Example 4: "Five less than half of a number is equal to 10"
Step 1: Let the unknown number be z.
Step 2: "Half of a number" is z/2.
Step 3: "Five less than" means we subtract 5: z/2 - 5
Step 4: Set this equal to 10.
Final equation: z/2 - 5 = 10
Example 5: "The product of a number and 6, increased by 4, is 28"
Step 1: Let the unknown number be w.
Step 2: "The product of a number and 6" is 6w.
Step 3: "increased by 4" means we add 4: 6w + 4
Step 4: Set this equal to 28.
Final equation: 6w + 4 = 28
When converting word sentences to algebra equations, follow these key steps:
- Identify the unknown quantity and assign it a variable.
- Translate words into mathematical operations (e.g., "sum" means addition, "product" means multiplication).
- Pay attention to the order of operations implied by the sentence.
- Look for words that indicate equality (e.g., "is," "equals," "results in") to form the equation.
Practice is essential to master this skill. Start with simple sentences and gradually move to more complex ones. Remember, creating equation models from word problems is a fundamental step in problem-solving and a valuable tool in various fields of study and real-world applications.
Conclusion
Variables in algebra are essential components that represent unknown values in mathematical expressions and equations. They serve as powerful tools for solving complex problems and modeling real-world scenarios. The introduction video provided a comprehensive overview of variables, their role in algebraic equations, and how they can be manipulated to find solutions. Understanding variables is crucial for mastering algebra and advancing in mathematics. By grasping this fundamental concept, students can tackle more advanced topics with confidence. The video emphasized the importance of practice in developing proficiency with variables and equations. We encourage you to engage with various algebra problems, applying the knowledge gained from the introduction video. Regular practice will enhance your problem-solving skills and deepen your understanding of algebraic concepts. Remember, variables are the building blocks of algebra, and mastering them opens doors to a wide range of mathematical applications in science, engineering, and everyday life.
Introduction to Variables in Algebra: What are equations?
In this lesson, we will explore the concept of equations in algebra, breaking down the key components and operations involved. Understanding equations is fundamental to mastering algebra, as they form the basis of many mathematical problems and solutions.
Step 1: Understanding the Basics of Equations
Equations are essentially math sentences. Just like sentences in English have structure and rules, equations in math follow specific guidelines. In an English sentence, you have words, capitalization, and punctuation. Similarly, in a math equation, you have terms (numbers or variables), operations (addition, subtraction, multiplication, division), and an answer.
Step 2: Components of an Equation
Every equation consists of several key components:
- Terms: These are the numbers or variables involved in the equation.
- Operations: The four basic operations used in equations are addition, subtraction, multiplication, and division.
- Answer: The result of the equation, which is what the equation is equal to.
For example, in the equation 2 + 3 = 5, the terms are 2 and 3, the operation is addition, and the answer is 5.
Step 3: Addition Equations
In addition equations, the terms being added are called addends, and the result is called the sum. For instance, in the equation 4 + 6 = 10, 4 and 6 are the addends, and 10 is the sum.
Step 4: Subtraction Equations
Subtraction equations involve a minuend and a subtrahend. The minuend is the number from which another number (the subtrahend) is subtracted, resulting in the difference. For example, in the equation 9 - 4 = 5, 9 is the minuend, 4 is the subtrahend, and 5 is the difference.
Step 5: Multiplication Equations
In multiplication equations, the numbers being multiplied are called factors, and the result is called the product. For example, in the equation 3 × 7 = 21, 3 and 7 are the factors, and 21 is the product.
Step 6: Division Equations
Division equations consist of a dividend and a divisor. The dividend is the number being divided, and the divisor is the number by which the dividend is divided. The result is called the quotient. For example, in the equation 20 ÷ 4 = 5, 20 is the dividend, 4 is the divisor, and 5 is the quotient.
Step 7: Summary of Key Terms
To summarize, here are the key terms associated with each type of equation:
- Addends: Terms in an addition equation.
- Sum: The result of an addition equation.
- Minuend: The number from which another number is subtracted in a subtraction equation.
- Subtrahend: The number that is subtracted in a subtraction equation.
- Difference: The result of a subtraction equation.
- Factors: Terms in a multiplication equation.
- Product: The result of a multiplication equation.
- Dividend: The number being divided in a division equation.
- Divisor: The number by which the dividend is divided in a division equation.
- Quotient: The result of a division equation.
Understanding these terms and how they relate to each type of equation is crucial for solving algebraic problems effectively.
FAQs
-
What is a variable in algebra?
A variable in algebra is a symbol, usually a letter like x or y, that represents an unknown value or a quantity that can change. Variables are used in mathematical expressions and equations to represent numbers whose values are not specified or can vary.
-
How do you solve equations with variables?
To solve equations with variables, you typically isolate the variable on one side of the equation. This is done by performing the same operations on both sides of the equation, such as adding, subtracting, multiplying, or dividing. The goal is to get the variable alone on one side, which gives you its value.
-
What are some common keywords used in word problems for different mathematical operations?
Common keywords include: for addition - "sum," "total," "plus"; for subtraction - "difference," "minus," "less than"; for multiplication - "product," "times," "of"; and for division - "quotient," "divided by," "per." Recognizing these keywords helps in translating word problems into mathematical equations.
-
How do you convert word sentences to algebra equations?
To convert word sentences to algebra equations, first identify the unknown quantity and assign it a variable. Then, translate words into mathematical operations (e.g., "sum" means addition). Pay attention to the order of operations implied by the sentence, and look for words that indicate equality (e.g., "is," "equals") to form the equation.
-
Why are variables important in algebra and real-world applications?
Variables are crucial in algebra as they allow us to represent unknown or changing quantities, solve complex problems, and model real-world situations mathematically. They are used in various fields such as physics, engineering, and economics to express relationships between different quantities and solve practical problems.
Prerequisite Topics
Understanding variables in algebra is a fundamental concept that builds upon several key mathematical principles. To fully grasp this topic, it's crucial to have a solid foundation in various prerequisite areas. For instance, being familiar with unknown quantities in equations helps students recognize how variables represent unknown values in algebraic expressions.
A strong grasp of algebraic expressions is essential, as variables are often used within these expressions. Understanding how to manipulate and simplify expressions containing variables is a critical skill. Additionally, knowledge of the characteristics of polynomial graphs can provide visual context for how variables behave in different equations.
Proficiency in solving linear equations using addition and subtraction and solving linear equations using multiplication and division is crucial. These skills form the basis for manipulating equations containing variables. Moreover, understanding the order of operations (PEMDAS) is vital when working with complex expressions involving variables.
Real-world applications, such as distance and time questions in linear equations, demonstrate how variables are used to solve practical problems. This connection helps students appreciate the relevance of variables in everyday scenarios. For more advanced topics, familiarity with solving radical equations can be beneficial, as variables often appear within radical expressions.
Understanding the relationship between two variables is crucial for grasping how variables interact within equations and systems. This concept is fundamental to many areas of algebra and higher mathematics. Lastly, a solid foundation in the application of integer operations is essential, as variables often represent integer values in algebraic problems.
By mastering these prerequisite topics, students will be well-prepared to tackle the concept of variables in algebra. Each of these areas contributes to a comprehensive understanding of how variables function within mathematical expressions and equations, setting the stage for success in more advanced algebraic concepts.

