Basics of solving equations with variables

In this lesson, we will learn:

• How to isolate the variable in an equation by using equation models, or by doing the operation to both sides to rearrange equations
• How to understand multiplication and division questions using the phrase “times as many” with the “times as many’ model

Notes:

• A systematic way to solve equations and find unknown variables is to isolate the variable:
• We want the unknown variable by itself on one side of the equal sign (=) and only numbers on the other side so that the operation can be completed

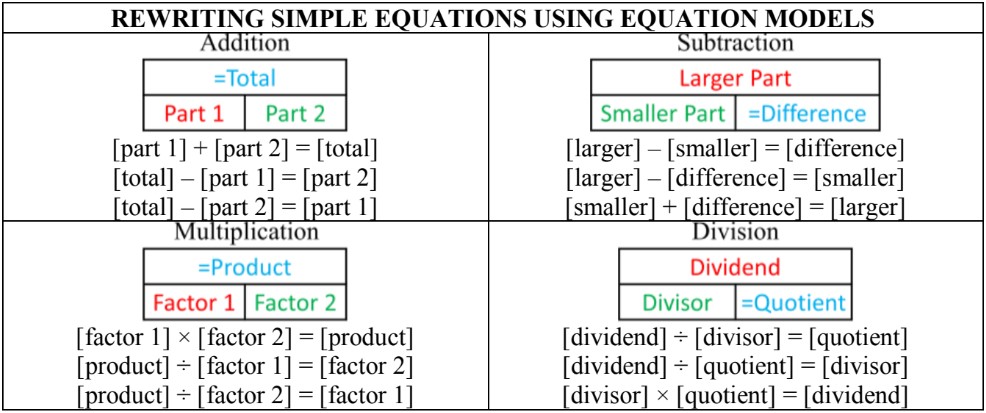
• Recall the equation models for the four operations. Equation models can help rearranging parts of an equation to isolate the variable. Any simple equation can be rewritten in 3 ways. Out of the three ways, one version will have the unknown variable by itself.

• When equation parts are side by side, you will be adding/multiplying; when equation parts are on top of each other, you will be subtracting/dividing

• You can also isolate the variable by “doing the opposite
  operation to both sides”: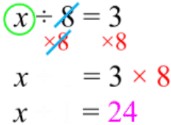


• Word problems using the phrase “times as many” may need multiplication or division:
• Use the “times as many” model to decide which operation to use