Characteristics of quadratic functions
All in One PlaceEverything you need for JC, LC, and college level maths and science classes. | Learn with EaseWe’ve mastered the national curriculum so that you can revise with confidence. | Instant Help24/7 access to the best tips, walkthroughs, and practice exercises available. |
Make math click 🤔 and get better grades! 💯Join for Free
0/10
Examples
Lessons
- Determining the Characteristics of a Quadratic Function Using Various Methods
Determine the following characteristics of the quadratic function :
• Opening of the graph
• intercept
• intercept(s)
• Vertex
• Axis of symmetry
• Domain
• Range
• Minimum/Maximum value
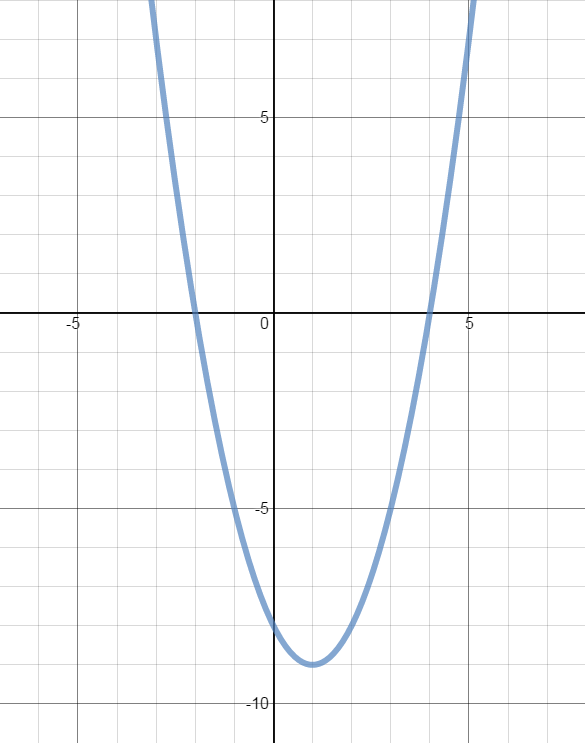
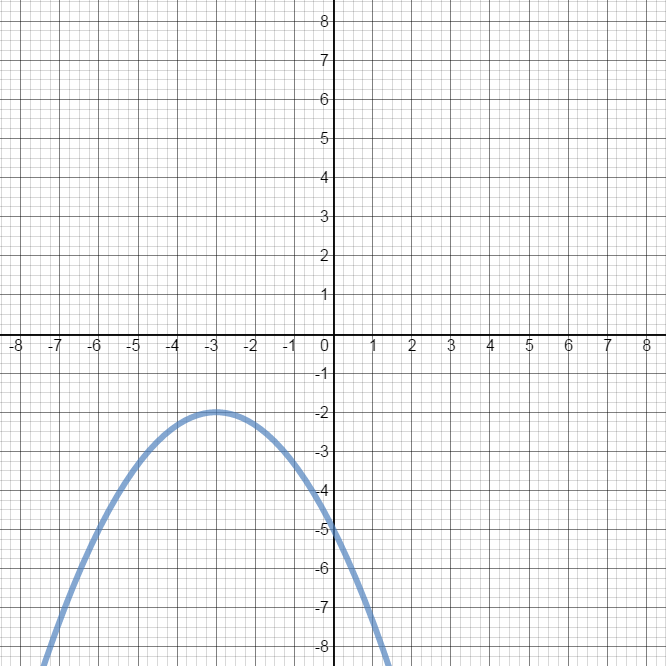
- From the graph of the parabola, determine the:
• vertex
• axis of symmetry
• y-intercept
• x-intercepts
• domain
• range
• minimum/maximum value
- Identifying Characteristics of Quadratic function in General Form:
is a quadratic function in general form.
i) Determine:
• y-intercept
• x-intercepts
• vertex
ii) Sketch the graph.
- Identifying Characteristics of Quadratic Functions in Vertex Form:
is a quadratic function in vertex form.
i) Determine:
• y-intercept
• x-intercepts
• vertex
ii) Sketch the graph.