Comparing and ordering decimals and fractions
Topic Notes
In this lesson, we will learn:
- How to compare decimals with decimals as well as fractions with fractions
- How to compare decimals with fractions using a number line or by converting into the same format
- How to order 3 or more decimals and fractions
Notes:
- When you compare two numbers, you always start with the biggest place value (most left) and then keep moving to the right (smaller place values) until you see a difference (the digits are different numbers).
- You compare numbers the same way for both whole numbers and decimals.
- For the numbers in each place value, 0 is the smallest and 9 is the biggest.
- Once you have found a difference for a place value, it does not matter what numbers are in the places further on the right (smaller places)
- The biggest place value (most left) that is different for the two numbers is what matters.
- Whenever you compare two numbers you need them to be in the same format; you will want to compare decimal vs. decimal (with same amount of place values) or fraction vs. fraction.
- To compare fractions with fractions
- Convert decimal numbers into fractions (have all fractions)
- Convert fractions into equivalent fractions with the same denominator
- Then, compare the numerators
- Ex. for vs. , you can either consider: vs. or vs.
- To compare decimals with decimals
- Convert fractions into decimals (have all decimal numbers)
- If youre having trouble comparing decimals of different lengths, make all the numbers have the same number of decimal places by add trailing zeroes (add zeroes to the right)
- Then, compare the decimals
- Seeing where common fractions and decimals are placed on a number line can help you to understand ordering decimals in fractions:
- First, we can divide a number line into halves:
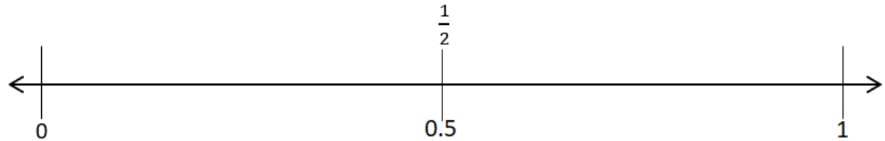
- Then, we can split each half into halves, making them quarters:
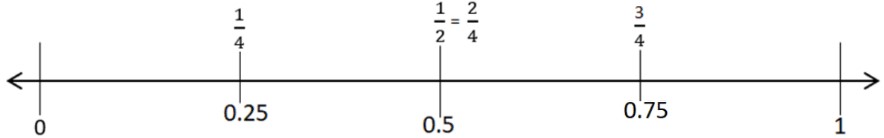
- We can also split a number line into tenths (ten pieces):

- We can further split number lines into hundredths by splitting each tenth into ten more pieces:
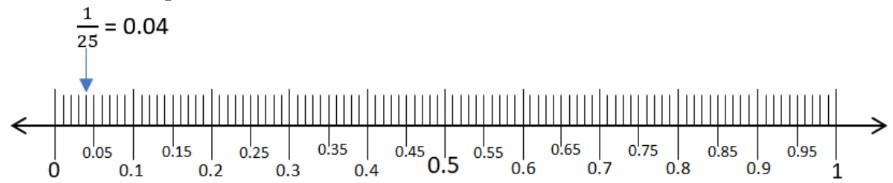
- To order a list of decimals and/or fractions, you must first convert them into the same format so that you can compare them. Then, follow the instructions of ordering either from:
- Least to greatest (increasing; smallest to biggest) or
- Greatest to least (decreasing; biggest to smallest)
- Review these symbols for comparing and ordering numbers:
- < less than
- > greater than
- = equal to
Introduction: Comparing and Ordering Decimals and Fractions
Welcome to our lesson on comparing and ordering fractions! This fundamental skill is crucial for advancing your mathematical understanding. We'll start with an introduction video that provides a clear, visual explanation of these concepts. This video is essential as it lays the groundwork for more complex operations involving decimals and fractions. When comparing decimals, we'll learn to align decimal points and compare digits from left to right. For fractions, we'll explore techniques like finding common denominators or converting to decimals. Ordering these numbers involves arranging them from least to greatest or vice versa. As we progress, you'll discover how these skills apply to real-world scenarios, making math more relatable and practical. Remember, mastering these basics will significantly boost your confidence in tackling more advanced math problems. So, let's dive in and start with our informative introduction video!
Understanding the process of ordering fractions is essential for solving many mathematical problems. By learning to arrange numbers from least to greatest, you can simplify complex equations and enhance your problem-solving skills. This knowledge is not only useful in academic settings but also in everyday life, where you might need to compare quantities or make decisions based on numerical data.
Understanding Place Values in Decimals and Fractions
Hey there! Let's dive into the fascinating world of place values in decimals and fractions. It's like a secret code that helps us understand and compare numbers easily. Ready to unlock this mathematical mystery?
First, let's start with whole numbers. You probably already know that in 352, the 3 is in the hundreds place, 5 is in the tens place, and 2 is in the ones place. Each digit has a specific value based on its position. Now, let's extend this idea to decimals!
Imagine a decimal point as a magical divider. To the left, we have whole numbers, and to the right, we enter the realm of fractions. The first place to the right of the decimal point is called tenths. Why? Because it represents one-tenth of a whole. For example, in 0.7, the 7 is in the tenths place.
Moving one step further to the right, we encounter hundredths. This place represents one-hundredth of a whole. In 0.25, the 2 is in the tenths place, and the 5 is in the hundredths place. It's like slicing a pizza into 100 tiny pieces!
Next up, we have thousandths. You guessed it this place represents one-thousandth of a whole. In 0.384, the 4 is in the thousandths place. Imagine dividing something into 1000 equal parts that's how small a thousandth is!
Now, let's put this knowledge to use in comparing place values. When we compare decimals, we look at each place value from left to right. For instance, let's compare 0.75 and 0.8:
- First, look at the tenths place. 7 tenths vs 8 tenths. Since 8 is greater than 7, 0.8 is larger than 0.75.
- If the tenths were the same, we'd move to the hundredths, and so on.
Here's another example: 0.362 vs 0.36
- The tenths (3) are the same for both.
- The hundredths (6) are also the same.
- In the thousandths place, 0.362 has a 2, while 0.36 has no digit (which is the same as 0).
- Since 2 is greater than 0, 0.362 is larger than 0.36.
This method works for comparing fractions too! Let's convert 3/4 and 5/8 to decimals:
- 3/4 = 0.75
- 5/8 = 0.625
Now we can compare them easily: 0.75 is greater than 0.625, so 3/4 is greater than 5/8.
Remember, each place value to the right of the decimal point is 10 times smaller than the one to its left. This pattern continues infinitely, giving us millionths, billionths, and beyond!
Practice comparing place values by lining up the decimal points and comparing each place value from left to right. With time, you'll become a pro at understanding and comparing fractions using place values. It's like having a superpower in the world of numbers!
Comparing Decimals: Techniques and Strategies
Comparing decimals is an essential skill in mathematics that requires a clear understanding of place value and decimal notation. This process involves aligning decimal points and comparing place values. Let's explore the steps and techniques for comparing decimals effectively.
Aligning Decimal Points
The first crucial step in comparing decimals is to align their decimal points. This alignment ensures that we compare digits in the same place value positions. For example, when comparing 0.75 and 0.8, we align the decimal points like this:
0.75
0.80
Notice that we added a zero to the right of 0.8 to make the comparison clearer. This doesn't change the value of the number but helps in the comparison process.
Comparing Place Values
Once the decimal points are aligned, we compare the digits in each place value from left to right. Start with the tenths, then hundredths, and so on. The first place where the digits differ determines which decimal is greater. In our example:
- The tenths are the same (7 and 8)
- In the hundredths place, 5 is less than 8
- Therefore, 0.75 < 0.80 (or 0.8)
Comparing Decimals with Different Numbers of Decimal Places
When comparing decimals with different numbers of decimal places, the alignment process becomes even more critical. Consider comparing 0.5 and 0.75:
0.50
0.75
We add a zero to 0.5 in the hundredths place to facilitate comparison. Now we can easily see that 0.5 < 0.75.
Practice Problems
To reinforce your understanding, try these practice problems:
- Compare 0.63 and 0.7
- Which is greater: 1.05 or 1.5?
- Order these decimals from least to greatest: 0.2, 0.15, 0.205
Tips for Comparing Decimals
- Always align decimal points first
- Add zeros to the right of the decimal if needed for alignment
- Compare digits from left to right
- Remember that more decimal places don't necessarily mean a larger number
Common Mistakes to Avoid
Be cautious of these common errors when comparing decimals:
- Forgetting to align decimal points
- Assuming a number with more decimal places is always larger
- Ignoring trailing zeros (e.g., thinking 0.5 and 0.50 are different)
Real-World Applications
Understanding how to compare decimals is crucial in many real-life situations, such as:
- Comparing prices when shopping
- Analyzing scientific measurements
- Evaluating sports statistics
By mastering the technique of comparing place values, you'll enhance your mathematical skills and improve your ability to make informed decisions in various aspects of life. Remember to practice regularly and apply these concepts to real-world scenarios to solidify your understanding.
Conclusion
Comparing decimals is a fundamental skill that builds on your understanding of place value and decimal notation. By following the steps of
Comparing Fractions: Methods and Approaches
Comparing fractions is an essential skill in mathematics that helps us understand and work with numbers in various real-life situations. Whether you're dividing a pizza among friends or measuring ingredients for a recipe, knowing how to compare fractions is incredibly useful. Let's explore some friendly and effective methods to compare fractions, making this sometimes tricky topic a breeze!
One of the most common methods for comparing fractions with different denominators is finding common denominators. Imagine you have two fractions, 3/4 and 2/3. At first glance, it might be challenging to tell which one is larger. But don't worry! By finding a common denominator, we can make these fractions easier to compare. To do this, we multiply both the numerator and denominator of each fraction by the denominator of the other fraction. So, 3/4 becomes (3 × 3)/(4 × 3) = 9/12, and 2/3 becomes (2 × 4)/(3 × 4) = 8/12. Now we can easily see that 9/12 is greater than 8/12, so 3/4 is larger than 2/3. It's like magic, isn't it?
Another handy method for comparing fractions with different denominators is cross-multiplication. This technique is especially useful when you're dealing with fractions that have different denominators. Let's say we want to compare 5/8 and 7/12. To use cross-multiplication, we multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa. So, 5 × 12 = 60, and 7 × 8 = 56. Since 60 is greater than 56, we know that 5/8 is larger than 7/12. It's like a little math puzzle that helps us figure out which fraction is bigger!
When it comes to comparing fractions with different denominators, finding a common denominator or using cross-multiplication are both excellent choices. But sometimes, we can use our number sense to make quick comparisons. For example, if we're comparing 1/2 and 3/8, we know that 1/2 is equivalent to 4/8. Since 4/8 is clearly larger than 3/8, we can quickly determine that 1/2 is the larger fraction. This method works well when we're familiar with common fraction equivalents.
Now, let's talk about comparing mixed numbers. Mixed numbers are whole numbers combined with fractions, like 2 1/3 or 4 3/4. To compare mixed numbers, we can convert them to improper fractions first. For example, to compare 2 1/3 and 2 1/4, we'd convert them to 7/3 and 9/4 respectively. Then, we can use cross-multiplication or find a common denominator to compare them. In this case, cross-multiplying gives us 7 × 4 = 28 and 9 × 3 = 27, so we know that 2 1/3 is slightly larger than 2 1/4.
Remember, practice makes perfect when it comes to comparing fractions. Don't be discouraged if it seems tricky at first with time and practice, you'll become a fraction-comparing pro! Try using these methods in everyday situations, like comparing the sizes of pizza slices or the amounts of ingredients in recipes. You'll be surprised how often fraction comparisons come in handy in real life.
To make comparing fractions even more fun, you can turn it into a game. Create fraction cards and challenge your friends or family members to a "Which fraction is larger?" contest. Not only will this help you practice, but it'll also show you how comparing fractions can be enjoyable and engaging.
As you become more comfortable with these methods, you'll find that comparing fractions becomes second nature. You'll be able to quickly assess which fraction is larger or smaller, making math problems and real-world applications much easier to handle. Remember, every time you successfully compare fractions, you're building your mathematical skills and confidence. So keep at it, and soon you'll be a fraction comparison expert!
In conclusion, comparing fractions doesn't have to be intimidating.
Converting Between Decimals and Fractions
Understanding how to convert decimals to fractions and vice versa is a fundamental skill in mathematics. This guide will walk you through the process step-by-step, helping you master these conversions with ease.
Converting Decimals to Fractions
To convert a decimal to a fraction, follow these steps:
- Write the decimal as a fraction over 1.
- Multiply both the numerator and denominator by 10 for each decimal place value.
- Simplify the fraction if possible.
Example: Convert 0.75 to a fraction
- Step 1: 0.75 = 0.75/1
- Step 2: 0.75/1 = 75/100 (multiplied by 100/100)
- Step 3: 75/100 = 3/4 (simplified)
Converting Fractions to Decimals
To convert a fraction to a decimal, simply divide the numerator by the denominator:
Example: Convert 3/4 to a decimal
- 3 ÷ 4 = 0.75
Common Fraction and Decimal Equivalents
Some fractions have well-known decimal equivalents that are worth memorizing:
- 1/2 = 0.5
- 1/4 = 0.25
- 3/4 = 0.75
- 1/3 0.333 (repeating)
- 2/3 0.667 (repeating)
- 1/5 = 0.2
- 1/8 = 0.125
Dealing with Repeating Decimals
Some fractions result in repeating decimals. To convert these to fractions:
- Let x be the repeating decimal.
- Multiply both sides by a power of 10 to shift the decimal place value.
- Subtract the original equation from the new one.
- Solve for x.
Example: Convert 0.333... (repeating) to a fraction
- Let x = 0.333...
- 10x = 3.333...
- 10x - x = 3.333... - 0.333...
- 9x = 3
- x = 3/9 = 1/3
Practice Tips
To improve your skills in converting between decimals and fractions:
- Practice regularly with various numbers.
- Use real-world examples to make the concepts more relatable.
- Utilize online calculators to check your work.
- Create flashcards with common equivalents.
Remember, the key to mastering decimal and fraction conversions is understanding the relationship between them. Decimals are simply another way to represent fractions, with the denominator being a power of 10. By practicing these conversions regularly, you'll develop a strong foundation in mathematical operations and problem-solving skills.
Whether you're working on academic assignments, handling financial calculations, or solving everyday math problems, the ability to convert between decimals and fractions is essential. For more complex scenarios, such as simplifying fractions or converting repeating decimals to fractions, additional practice and understanding are required.
Ordering Decimals and Fractions on a Number Line
Welcome to the exciting world of ordering decimals and fractions on a number line! This powerful tool helps us visualize and compare numbers, making it easier to understand their relationships. Let's dive in and explore how to use a number line to order decimals and fractions from least to greatest and greatest to least.
Understanding the Number Line
A number line is a straight line with equally spaced points representing numbers. It extends infinitely in both directions, with numbers increasing as you move right and decreasing as you move left. This visual representation is perfect for comparing numbers on a number line.
Ordering Decimals on a Number Line
When working with decimals, it's essential to align the decimal points and compare digits from left to right. Let's practice with an example:
Order these decimals from least to greatest: 0.75, 0.8, 0.25, 0.308
- Draw a number line from 0 to 1, divided into tenths.
- Place each decimal on the line:
- 0.25 is halfway between 0.2 and 0.3
- 0.308 is just after 0.3
- 0.75 is three-quarters of the way between 0.7 and 0.8
- 0.8 is exactly at the 0.8 mark
- Read the numbers from left to right: 0.25, 0.308, 0.75, 0.8
Therefore, the order from least to greatest is: 0.25, 0.308, 0.75, 0.8
Ordering Fractions on a Number Line
Fractions can be trickier, but the number line makes it easier to visualize their relationships. Let's try an example:
Order these fractions from greatest to least: 1/2, 3/4, 1/3, 5/6
- Draw a number line from 0 to 1, divided into twelfths (the least common multiple of the denominators).
- Convert each fraction to an equivalent fraction with a denominator of 12:
- 1/2 = 6/12
- 3/4 = 9/12
- 1/3 = 4/12
- 5/6 = 10/12
- Place each fraction on the line and read from right to left: 5/6, 3/4, 1/2, 1/3
Therefore, the order from greatest to least is: 5/6, 3/4, 1/2, 1/3
Least to Greatest vs. Greatest to Least
"Least to greatest" means arranging numbers in ascending order, starting with the smallest and ending with the largest. On a number line, you read from left to right. "Greatest to least" is the opposite, arranging numbers in descending order, starting with the largest and ending with the smallest. On a number line, you read from right to left.
Practice Exercises
Try these exercises to reinforce your understanding:
- Order from least to greatest: 0.6, 0.06, 0.66, 0.606
- Order from greatest to least: 2/5, 1/2, 3/8, 5/8
- Mix it up! Order from least to greatest: 0.
Practical Applications and Real-World Examples
Understanding how to compare and order decimals and fractions isn't just about acing math tests it's a skill that comes in handy in many real-world situations! Let's explore some everyday scenarios where these mathematical concepts prove incredibly useful.
In the kitchen, cooking and baking often require precise measurements. Imagine you're following a recipe that calls for 3/4 cup of flour, but you only have a 1/2 cup measure. By understanding fractions, you can easily figure out that you need to fill the 1/2 cup, plus another 1/4 cup to get the right amount. Similarly, when doubling a recipe that requires 0.75 teaspoons of salt, you'll need to know that this equals 1.5 teaspoons.
Financial calculations are another area where comparing decimals and fractions is crucial. When shopping for the best deals, you might need to compare discounts. Is 25% off better than 1/3 off? By converting these to decimals (0.25 and approximately 0.33), you can quickly determine that 1/3 off is the better deal. In personal finance, understanding interest rates is essential. A savings account offering 2.5% interest might seem better than one offering 0.025, but they're actually the same the second is just expressed as a decimal instead of a percentage.
In home improvement projects, measurements often involve fractions and decimals. When cutting wood for shelving, you might need to divide a 6-foot board into 5 equal parts. This requires understanding that each piece should be 1.2 feet or 1 foot and 2.4 inches long. Similarly, when mixing paint colors, ratios are often given in fractions (like 1 part blue to 3 parts white), which you may need to convert to decimals for precise measurements.
Sports and fitness enthusiasts often encounter decimals and fractions too. Runners might compare their mile times: is 7.5 minutes per mile faster than 7 minutes and 35 seconds? By converting 35 seconds to a fraction of a minute (35/60 0.58), you can see that 7.5 minutes is indeed faster. In weight training, plates come in various weights like 2.5 lbs, 5 lbs, and 10 lbs. Calculating your total lift often involves adding these decimal weights.
Even in everyday travel, these skills come into play. When planning a road trip, you might need to calculate fuel efficiency. If your car uses 3/8 of a tank to travel 150 miles, how many miles per gallon is it getting? By converting fractions to decimals and doing some simple division, you can figure out your car's efficiency.
Remember, math isn't just about numbers on a page it's a powerful tool that helps us navigate our daily lives more effectively. By mastering the comparison and ordering of decimals and fractions, you're equipping yourself with skills that have countless practical applications. So next time you're working with these concepts, think about how they might apply to your everyday experiences. You'll be surprised at how often they come in handy!
Conclusion: Mastering Decimal and Fraction Comparisons
Mastering comparisons between decimals and fractions is a crucial skill in mathematics. We've covered key points including converting fractions to decimals, aligning decimal points, and using number lines for visual representation. Understanding these concepts allows for confident problem-solving in various mathematical scenarios. Remember, practice is essential for solidifying your skills. We encourage you to engage with additional resources and exercises to further enhance your abilities. Whether you're working on homework, preparing for exams, or applying these skills in real-life situations, the techniques we've discussed will prove invaluable. Don't hesitate to revisit this guide whenever you need a refresher. By consistently applying these methods, you'll develop a strong foundation in comparing and ordering decimals and fractions. Keep up the great work, and remember that each practice session brings you closer to mathematical mastery. Ready for more challenges? Explore our additional resources to take your skills to the next level!
Introduction to Comparing and Ordering Decimals and Fractions: How Do You Compare Two Numbers?
In this lesson, we will learn how to compare and order decimals and fractions. Understanding how to compare two numbers is essential for various mathematical operations and real-life applications. Let's break down the process step by step.
Step 1: Understanding the Concept of Comparing Numbers
Comparing two numbers means determining which number is larger and which is smaller. This process involves examining each digit of the numbers, starting from the leftmost digit (the highest place value) and moving to the right. The goal is to identify the first point of difference between the two numbers.
Step 2: Comparing Whole Numbers
Before diving into decimals and fractions, let's review how to compare whole numbers. Consider the numbers 342 and 332. To compare these numbers, follow these steps:
- Write down the numbers in a place value table, aligning the digits according to their place values (hundreds, tens, and ones).
- Start with the leftmost place value (hundreds). Compare the digits in this place value for both numbers. In this case, both numbers have a 3 in the hundreds place, so they are equal in this place value.
- Move to the next place value to the right (tens). Compare the digits in the tens place. Here, 342 has a 4, and 332 has a 3. Since 4 is greater than 3, we can conclude that 342 is greater than 332.
- There is no need to compare the ones place because we have already determined the larger number based on the tens place.
Step 3: Comparing Decimal Numbers
Now, let's compare decimal numbers. Consider the numbers 8.97 and 8.795. Follow these steps:
- Write down the numbers in a place value table, aligning the digits according to their place values (ones, tenths, hundredths, and thousandths).
- Start with the leftmost place value (ones). Compare the digits in this place value for both numbers. In this case, both numbers have an 8 in the ones place, so they are equal in this place value.
- Move to the next place value to the right (tenths). Compare the digits in the tenths place. Here, 8.97 has a 9, and 8.795 has a 7. Since 9 is greater than 7, we can conclude that 8.97 is greater than 8.795.
- There is no need to compare the hundredths and thousandths places because we have already determined the larger number based on the tenths place.
Step 4: General Rules for Comparing Numbers
When comparing numbers, whether they are whole numbers, decimals, or fractions, follow these general rules:
- Align the numbers according to their place values.
- Start with the leftmost place value and compare the digits in this place value for both numbers.
- If the digits are equal, move to the next place value to the right and compare the digits in this place value.
- Continue this process until you find a place value where the digits are different. The number with the larger digit in this place value is the larger number.
- If all the digits are equal, the numbers are equal.
Step 5: Practice with Examples
To solidify your understanding, practice comparing different sets of numbers. Here are a few examples to try:
- Compare 56.78 and 56.789
- Compare 123.45 and 123.456
- Compare 0.567 and 0.56
- Compare 45.6 and 45.60
By practicing these examples, you will become more comfortable with the process of comparing and ordering decimals and fractions.
FAQs
Here are some frequently asked questions about comparing and ordering decimals and fractions:
-
How do I compare decimals with different numbers of decimal places?
To compare decimals with different numbers of decimal places, first align the decimal points and add zeros to the right of the shorter decimal if needed. Then, compare the digits from left to right until you find a difference. For example, to compare 0.75 and 0.8, add a zero to 0.8 to make it 0.80, then compare 0.75 and 0.80.
-
What's the easiest way to compare fractions with different denominators?
One of the easiest ways to compare fractions with different denominators is to find a common denominator. Multiply both the numerator and denominator of each fraction by the denominator of the other fraction. Once you have a common denominator, you can directly compare the numerators. Alternatively, you can convert the fractions to decimals and compare the resulting decimal numbers.
-
How can I order a mix of decimals and fractions from least to greatest?
To order a mix of decimals and fractions, convert all numbers to the same form (either all decimals or all fractions). Converting to decimals is often easier. Once all numbers are in the same form, you can order them from least to greatest by comparing their values. Using a number line can be helpful for visualization.
-
What's the difference between comparing numbers and ordering numbers?
Comparing numbers involves determining which of two numbers is greater or if they are equal. Ordering numbers takes this a step further by arranging three or more numbers in a specific sequence, typically from least to greatest or greatest to least. Ordering requires multiple comparisons to determine the correct sequence.
-
How can I use a number line to compare and order fractions and decimals?
A number line is a great visual tool for comparing and ordering fractions and decimals. First, convert all numbers to the same form (decimals are often easier). Then, plot each number on the number line. Numbers further to the right are greater, while those to the left are lesser. Reading the plotted points from left to right gives you the order from least to greatest.
Prerequisite Topics
Understanding the foundation of mathematics is crucial when tackling more advanced concepts like comparing and ordering decimals and fractions. To excel in this area, it's essential to grasp several key prerequisite topics that form the building blocks of numerical comprehension.
One of the most fundamental concepts is place value. This concept is vital for comparing place values in both whole numbers and decimals. When you understand how each digit's position affects its value, you can more easily compare and order numbers, especially when dealing with decimals of different lengths.
Another important skill is simplifying fractions. This process helps in reducing fractions to their simplest form, making it easier to compare them with other fractions or decimals. Being able to simplify complex fractions is particularly useful when dealing with mixed numbers or improper fractions.
Speaking of mixed numbers, comparing mixed numbers is another crucial skill. Understanding how to work with mixed numbers, including converting them to improper fractions, is essential for accurately comparing and ordering fractions of different types.
When it comes to putting numbers in order, mastering the skill of ordering numbers on a number line is invaluable. This visual representation helps in understanding the relative positions of different numbers, whether they're whole numbers, fractions, or decimals.
Lastly, the ability to convert between different number representations is crucial. Specifically, converting repeating decimals to fractions is a key skill. This conversion allows for easier comparison between fractions and decimals, especially when dealing with recurring decimal expansions.
By mastering these prerequisite topics, students build a strong foundation for comparing and ordering decimals and fractions. Each concept contributes to a deeper understanding of number relationships and provides essential tools for mathematical problem-solving. As students progress, they'll find that these fundamental skills continually resurface, reinforcing their importance in more advanced mathematical concepts.

