Comparing and ordering large multi-digit integers
Topic Notes
In this lesson, we will learn:
- To compare integers—positive and negative whole numbers—up to millions place values
- To order a list of integers—positive and negative whole numbers—up to millions place values
Notes:
- When comparing numbers, we use the symbols:
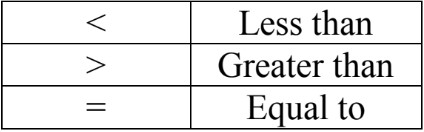
- For integers, use a number line to understand which numbers are bigger or smaller
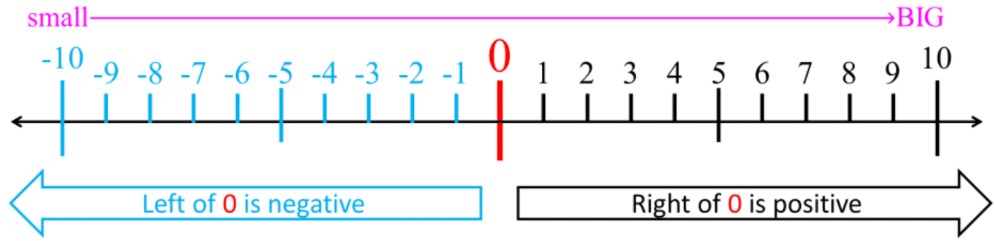
- Smaller numbers are to the left; bigger numbers are to the right
- Ex. Look at the pairs of opposite numbers: -5 < -2 vs. 5 > 2
- For negative numbers: the bigger the negative, the smaller the value (i.e. more negative means less value)

- The same rules apply for comparing multi-digit integers:
- Ex. Compare the number -5000 with: 6000, 5000, 0, and -6000

- -5000 < 6000
- -5000 < 5000
- -5000 < 0
- -5000 < 6000
- There are two ways to order a list of numbers, including multi-digit integers:
- From least to greatest (smallest to biggest)
- most negative to least negative
- From greatest to least (biggest to smallest)
- least negative to most negative
- Ex. -6000 < -5000 < 0 < 5000 < 6000
Introduction to Comparing and Ordering Multi-Digit Integers
Welcome to our lesson on comparing and ordering large multi-digit integers! This fundamental skill is crucial for advancing your mathematical abilities. To kick things off, we've prepared an introduction video that will give you a solid foundation for understanding these concepts. The video covers essential strategies for comparing numbers with multiple digits and arranging them in order. By watching it, you'll gain valuable insights into how to approach these problems efficiently. Remember, when dealing with multi-digit integers, we need to look at more than just the first digit. We'll explore techniques like comparing place values, using number lines, and applying logical reasoning to determine which number is greater or smaller. As we progress, you'll learn how to confidently order a series of large numbers, a skill that's incredibly useful in various mathematical applications and real-world scenarios. Let's dive in and master the art of comparing and ordering multi-digit integers together!
Understanding Integers and Number Lines
What Are Integers?
Integers are whole numbers that include both positive and negative numbers, as well as zero. They are a fundamental concept in mathematics and are used in countless real-world applications. Integers can be represented on a number line, which helps visualize their relationships and order.
Positive Integers
Positive integers are whole numbers greater than zero. They are located to the right of zero on a number line and include numbers like 1, 2, 3, and so on. These numbers represent quantities or values that are above or more than zero.
Negative Integers
Negative integers are whole numbers less than zero. They are located to the left of zero on a number line and include numbers like -1, -2, -3, and so on. Negative numbers represent quantities or values that are below or less than zero, such as temperatures below freezing or debts.
Zero: The Neutral Integer
Zero is a unique integer that is neither positive nor negative. It serves as the central point on the number line, separating positive and negative numbers. Zero represents the absence of quantity or a neutral value.
Using a Number Line to Visualize Integers
A number line is a powerful tool for understanding and comparing integers. It is a horizontal line with equally spaced markings representing integers. The number line extends infinitely in both directions, with positive numbers to the right of zero and negative numbers to the left.
Key Features of a Number Line:
- Zero is at the center
- Positive numbers increase to the right
- Negative numbers decrease to the left
- Equal intervals between consecutive integers
Comparing Integers on a Number Line
The number line makes it easy to compare integers visually. Numbers to the right are always greater than numbers to the left. This principle applies to both positive and negative numbers.
Examples of Comparing Integers:
- 5 > 3 (5 is to the right of 3 on the number line)
- -2 > -5 (-2 is to the right of -5)
- 0 > -7 (0 is to the right of all negative numbers)
- 4 > -1 (All positive numbers are to the right of negative numbers)
Absolute Value and Distance on the Number Line
The absolute value of integers is its distance from zero on the number line, regardless of whether it's positive or negative. For example, both 3 and -3 have an absolute value of integers of 3, as they are both 3 units away from zero on the number line.
Practical Applications of Integers
Understanding integers is crucial for many practical applications of integers:
- Banking: Account balances (positive for savings, negative for overdrafts)
- Temperature: Above and below freezing point
- Elevation: Above and below sea level
- Sports: Scoring and statistics
Conclusion
Integers, including positive and negative numbers, are essential components of mathematics. The number line serves as a valuable visual aid for understanding and comparing these numbers. By mastering the concept of integers and their representation on a number line, students build a strong foundation for more advanced mathematical concepts and practical applications of integers.
Comparing Large Multi-Digit Integers
Comparing large multi-digit integers, whether positive or negative, is an essential skill in mathematics. This process relies heavily on understanding place value and applying it systematically. Let's break down the steps and explore how to compare these numbers effectively.
First, let's review the concept of place value. In our number system, each digit's position determines its value. For example, in the number 3,456, we have:
- 3 in the thousands place
- 4 in the hundreds place
- 5 in the tens place
- 6 in the ones place
Understanding place value is crucial when comparing multi-digit integers. Now, let's look at the step-by-step process for comparing these numbers:
- Compare the signs: If one number is positive and the other is negative, the positive number is always greater. For example, 100 is greater than -1,000,000.
- Compare the number of digits: If both numbers have the same sign, look at the number of digits. The number with more digits is larger for positive numbers and smaller for negative numbers. For instance, 1,000 is greater than 999, while -1,000 is less than -999.
- Compare digits from left to right: If the numbers have the same number of digits, start comparing from the leftmost digit (the highest place value). The number with the larger digit in the first differing position is greater for positive numbers and smaller for negative numbers.
Let's practice with some examples:
Example 1: Compare 45,678 and 45,698
- Both numbers are positive and have the same number of digits.
- The first three digits (45,6) are the same.
- In the tens place, 7 < 9.
- Therefore, 45,678 < 45,698.
Example 2: Compare -123,456 and -123,654
- Both numbers are negative and have the same number of digits.
- The first three digits (-123) are the same.
- In the hundreds place, 4 < 6.
- For negative numbers, the smaller digit means a larger number.
- Therefore, -123,456 > -123,654.
Example 3: Compare 1,000,000 and 999,999
- Both numbers are positive.
- 1,000,000 has 7 digits, while 999,999 has 6 digits.
- The number with more digits is larger.
- Therefore, 1,000,000 > 999,999.
When dealing with very large numbers, it's helpful to use commas or spaces to separate groups of three digits. This makes it easier to identify place values quickly. For instance, 1,234,567,890 is more readable than 1234567890.
Remember, when comparing negative numbers, the rules are reversed. The number closer to zero is considered greater. For example, -100 is greater than -1,000, even though 100 is less than 1,000 when they're positive.
Practice is key to mastering the comparison of multi-digit integers. Start with smaller numbers and gradually work your way up to larger ones. As you become more comfortable, you'll find that you can quickly compare even very large numbers at a glance.
In real-world applications, comparing large multi-digit integers is crucial in various fields such as finance, science, and technology.
Ordering Large Multi-Digit Integers
Ordering large multi-digit integers is an essential skill in mathematics and everyday life. Whether you're dealing with positive or negative numbers, understanding how to arrange them from least to greatest or greatest to least is crucial. Let's explore various methods and examples to master this concept.
When ordering positive multi-digit integers from least to greatest:
- Compare the number of digits: Numbers with fewer digits are smaller.
- If the numbers have the same digit count, compare from left to right.
- The first differing digit determines the order.
Example: Order 1234, 987, 10001, 9999 from least to greatest
Result: 987 < 1234 < 9999 < 10001
For ordering positive integers from greatest to least, simply reverse this process.
When dealing with negative numbers, remember:
- Negative numbers are always less than positive numbers.
- For negative numbers, a larger absolute value means a smaller number.
Example: Order -5678, -123, -9999, -1 from least to greatest
Result: -9999 < -5678 < -123 < -1
Handling mixed lists of positive and negative integers requires extra attention:
- Separate positive and negative numbers.
- Order positive numbers from least to greatest.
- Order negative numbers from greatest to least (remember, -1 is greater than -10).
- Combine the lists, with negative numbers first.
Example: Order -100, 50, -25, 75, 0, -50 from least to greatest
Step 1: Separate: (-100, -25, -50) and (50, 75, 0)
Step 2: Order negatives: -100 < -50 < -25
Step 3: Order positives: 0 < 50 < 75
Step 4: Combine: -100 < -50 < -25 < 0 < 50 < 75
For greatest to least ordering of mixed lists:
- Follow the same separation process.
- Order positive numbers from greatest to least.
- Order negative numbers from least to greatest.
- Combine, with positive numbers first.
Example: Order -200, 150, -75, 225, 0, -100 from greatest to least
Result: 225 > 150 > 0 > -75 > -100 > -200
When working with very large numbers, it's helpful to use place value understanding:
- Compare the leftmost digits first.
- If they're the same, move to the next digit.
- Continue until you find a difference or reach the end.
Example: Order 1,234,567 and 1,234,765 from least to greatest
Compare: 1 = 1, 2 = 2, 3 = 3, 4 = 4, 5 = 5, 6 < 7
Result: 1,234,567 < 1,234,765
Strategies for Comparing and Ordering Negative Integers
Comparing and ordering negative integers can be a challenging concept for many students. Unlike positive numbers, where a larger number is considered "greater," negative numbers follow a different logic. Understanding how to navigate this realm of mathematics is crucial for developing a strong foundation in number sense and algebraic thinking.
When dealing with negative integers, it's essential to grasp the concepts of "more negative" and "less negative." A number that is more negative is actually smaller in value, while a less negative number is larger. For instance, -5 is more negative than -3, making -5 the smaller number. This counterintuitive relationship often confuses learners who are accustomed to thinking of larger numbers as greater.
One effective strategy for comparing negative numbers is to visualize them on a number line. Numbers to the left are always smaller than numbers to the right. This visual representation helps students understand that as we move further left into negative territory, the numbers become smaller (more negative). For example, -7 is to the left of -4 on the number line, so -7 is smaller than -4.
Another helpful tip is to focus on the absolute value of the numbers. The number with the larger absolute value is more negative when dealing with negative integers. For instance, when comparing -8 and -3, we can look at their absolute values: |-8| = 8 and |-3| = 3. Since 8 is greater than 3, -8 is more negative (and thus smaller) than -3.
When ordering a set of negative integers, it can be useful to arrange them from least negative to most negative (which is the same as arranging them from largest to smallest). For example, given the numbers -2, -9, -5, and -1, we would order them as follows: -1, -2, -5, -9. This order places the numbers from closest to zero (least negative) to furthest from zero (most negative).
To reinforce these concepts, let's consider some practice examples:
1. Compare -6 and -2: -6 is more negative than -2, so -6 < -2.
2. Order from least to greatest: -8, -3, -11, -5: -11, -8, -5, -3
3. Which is greater, -4 or -7? -4 is greater because it's less negative.
4. Find the smallest number: -1, -10, -5, -8: -10 is the smallest (most negative).
Remember, when working with negative numbers, terms like "greater than" and "less than" can be confusing. It's often helpful to rephrase questions using "more negative" or "less negative" to clarify the relationship between numbers. For instance, instead of asking "Which is greater, -9 or -2?" you could ask "Which is less negative, -9 or -2?"
As students become more comfortable with these concepts, they can apply them to more complex mathematical operations. Understanding how to compare and order negative integers is fundamental for solving equations, graphing functions, and working with coordinate planes in higher-level mathematics.
In conclusion, mastering the comparison and ordering of negative integers requires a shift in thinking from how we typically approach positive numbers. By utilizing strategies such as number line visualization, focusing on absolute values, and practicing with various examples, students can develop a strong intuition for working with negative numbers. This skill is not only crucial for academic success in mathematics but also for real-world applications in fields such as finance, physics, and data analysis.
Real-World Applications and Practice Problems
Comparing and ordering large multi-digit integers is a crucial skill with numerous real-world applications. From finance to science, this ability helps us make informed decisions and solve complex problems. Let's explore some scenarios and practice problems to enhance our understanding.
Real-World Applications
- Population Statistics: Comparing populations of different countries or cities.
- Financial Analysis: Ordering company revenues or stock prices.
- Scientific Research: Comparing distances in astronomy or particle sizes in physics.
- Sports Statistics: Ranking athletes based on performance metrics.
- Technology: Comparing processor speeds or storage capacities.
Practice Problems
Let's dive into some practice problems to hone our skills:
Problem 1: Population Comparison
Order these countries by population (largest to smallest):
- India: 1,393,409,038
- United States: 332,915,073
- Indonesia: 276,361,783
- Pakistan: 220,892,340
Solution: India > United States > Indonesia > Pakistan
Problem 2: Financial Analysis
Arrange these company revenues in ascending order:
- Company A: $78,945,621,300
- Company B: $78,945,621,301
- Company C: $78,945,621,299
- Company D: $78,945,621,302
Solution: Company C < Company A < Company B < Company D
Problem 3: Astronomical Distances
Which star is closest to Earth? (Distance in kilometers)
- Proxima Centauri: 40,000,000,000,000
- Alpha Centauri A: 41,320,000,000,000
- Sirius: 81,360,000,000,000
Solution: Proxima Centauri is the closest.
Problem 4: Sports Statistics
Rank these basketball players by total career points scored:
- Player A: 38,387
- Player B: 38,390
- Player C: 36,928
- Player D: 38,385
Try solving this one on your own!
Problem 5: Technology Comparison
Order these hard drive capacities from smallest to largest:
- 2 terabytes
- 1,500,000 megabytes
- 3,000,000,000,000 bytes
- 2,500 gigabytes
Hint: Convert all values to the same unit before comparing.
These practice problems cover various aspects of comparing and ordering multi-digit integers. Remember to align digits properly when comparing, and don't forget about place value. For large numbers, it can be helpful to compare digit by digit from left to right. Keep practicing to improve your skills in this essential mathematical concept!
Conclusion
In summary, this article has covered essential key points to enhance your understanding of the subject matter. The introduction video serves as a crucial foundation, providing visual and auditory explanations that complement the written content. We've explored various aspects of the topic, highlighting important concepts and practical applications. Remember, regular practice is key to mastering these skills. We encourage you to revisit the material, especially the introduction video, to reinforce your learning. As you progress, consider exploring additional resources for further learning and deeper insights. Don't hesitate to engage with our community, ask questions, and share your experiences. Your journey doesn't end here take the next step by applying these concepts in real-world scenarios. Stay curious, keep practicing, and continue to expand your knowledge in this fascinating field. We're excited to see how you'll apply these learnings in your future endeavors!
Introduction to Comparing and Ordering Large Multi-Digit Integers: How to Compare Two Large Multi-Digit Integers (Positive and Negative)
In this guide, we will explore the process of comparing and ordering large multi-digit integers, both positive and negative. This involves understanding the use of comparison symbols and the concept of negative and positive integers on a number line.
Step 1: Understanding Comparison Symbols
When comparing numbers, we use three primary symbols: less than (<), greater than (>), and equal to (=). These symbols help us determine the relationship between two numbers. The less than symbol (<) indicates that the number on the left is smaller than the number on the right. The greater than symbol (>) indicates that the number on the left is larger than the number on the right. The equal to symbol (=) is used when two numbers are exactly the same.
To remember how the less than and greater than symbols work, think of a hungry alligator that always wants to eat the bigger number. The open side of the symbol (the alligator's mouth) always points towards the larger number.
Step 2: Introduction to Integers
Integers include all positive and negative whole numbers, as well as zero. When we talk about integers, we often use a number line to visualize their positions. On a number line, negative numbers are to the left of zero, and positive numbers are to the right. The further left a number is, the smaller its value. Conversely, the further right a number is, the larger its value.
For example, on a number line from -10 to 10, -2 is to the left of 2, indicating that -2 is smaller than 2. Similarly, -5 is to the left of -2, indicating that -5 is smaller than -2.
Step 3: Comparing Positive Integers
When comparing positive integers, the process is straightforward. The number with more digits or the higher value is larger. For instance, comparing 2 and 5, we know that 5 is larger because it is further to the right on the number line.
Similarly, when comparing larger multi-digit integers, such as 1234 and 5678, we see that 5678 is larger because it has a higher value.
Step 4: Comparing Negative Integers
Comparing negative integers can be a bit counterintuitive. The more negative a number is, the smaller its value. For example, -5 is smaller than -2 because -5 is further to the left on the number line. This means that -5 is less than -2.
When comparing larger negative integers, such as -1000 and -500, -1000 is smaller because it is more negative and further to the left on the number line.
Step 5: Combining Positive and Negative Integers
When comparing a positive integer with a negative integer, the positive integer is always larger. For example, comparing 5 and -5, 5 is larger because it is on the right side of zero, while -5 is on the left side.
Similarly, comparing 1000 and -1000, 1000 is larger because it is a positive number, while -1000 is a negative number.
Step 6: Using a Number Line for Large Multi-Digit Integers
To compare large multi-digit integers, we can use a number line to visualize their positions. For example, if we have -5000 and 5000, we know that 5000 is larger because it is on the right side of zero, while -5000 is on the left side.
When comparing two large negative integers, such as -5000 and -6000, -6000 is smaller because it is more negative and further to the left on the number line.
Step 7: Summary
In summary, when comparing and ordering large multi-digit integers, remember the following key points:
- Use the less than (<), greater than (>), and equal to (=) symbols to compare numbers.
- Positive integers are always larger than negative integers.
- Among negative integers, the more negative a number is, the smaller its value.
- Use a number line to visualize the positions of integers and compare their values.
By following these steps, you can accurately compare and order large multi-digit integers, both positive and negative.
FAQs
-
Q: How do I compare two large multi-digit integers?
A: To compare large multi-digit integers, follow these steps:
- Compare the signs (positive or negative).
- If the signs are the same, compare the number of digits.
- If the number of digits is the same, compare digit by digit from left to right until you find a difference.
Remember, for positive numbers, the larger digit means a greater number. For negative numbers, the smaller digit means a greater number (closer to zero).
-
Q: What's the easiest way to order negative integers?
A: To order negative integers, remember that numbers closer to zero are greater. You can use these methods:
- Visualize them on a number line, with numbers to the right being greater.
- Compare their absolute values; the number with the smaller absolute value is greater.
- When ordering from least to greatest, arrange them from the most negative to the least negative.
-
Q: How does place value help in comparing large numbers?
A: Place value is crucial when comparing large numbers. Start by comparing the digits in the highest place value (leftmost digit). If these are the same, move to the next place value to the right. Continue this process until you find a difference. The number with the larger digit in the first differing place value is greater.
-
Q: Can you explain how to compare numbers with different numbers of digits?
A: When comparing numbers with different numbers of digits:
- For positive numbers, the number with more digits is always greater.
- For negative numbers, the number with more digits is always smaller (more negative).
- If comparing a positive and a negative number, the positive number is always greater, regardless of the number of digits.
-
Q: What are some real-world applications of comparing and ordering large integers?
A: Comparing and ordering large integers has many practical applications:
- Financial analysis: Comparing company revenues, stock prices, or national debts.
- Population statistics: Ranking countries or cities by population.
- Scientific research: Comparing astronomical distances or microscopic measurements.
- Technology: Evaluating computer processing speeds or data storage capacities.
- Sports: Ranking athletes based on performance statistics.
Prerequisite Topics
Understanding the foundation of mathematics is crucial when tackling more complex concepts like comparing and ordering large multi-digit integers. To excel in this area, it's essential to grasp several key prerequisite topics that form the building blocks of numerical comprehension.
One of the most fundamental concepts to master is place value. This principle is the cornerstone of our number system, determining the value of each digit based on its position within a number. When dealing with large multi-digit integers, a solid understanding of place value becomes even more critical. It allows students to accurately interpret the magnitude of each digit, which is essential for comparing and ordering these numbers effectively.
Building upon place value, the skill of comparing and ordering numbers is directly applicable to working with large integers. This prerequisite topic introduces the basic principles of numerical comparison, which are then scaled up when dealing with multi-digit numbers. Students learn to use greater than, less than, and equal to symbols, as well as strategies for systematically comparing numbers of different sizes.
While it may seem less obvious, understanding absolute value functions can also play a role in comparing large integers, especially when negative numbers are involved. The concept of absolute value helps students grasp the true magnitude of a number, regardless of its sign. This becomes particularly useful when ordering a mix of positive and negative large integers.
Lastly, the practical applications of integers provide context and relevance to the skill of comparing and ordering large numbers. By understanding how these concepts are used in real-world scenarios, such as in financial calculations, scientific measurements, or population statistics, students can better appreciate the importance of accurately working with multi-digit integers.
Mastering these prerequisite topics creates a strong foundation for students to confidently approach the challenge of comparing and ordering large multi-digit integers. Each concept builds upon the others, forming a comprehensive understanding that enables students to tackle more complex mathematical problems with ease. By recognizing the interconnectedness of these topics, learners can develop a more holistic view of mathematics and its applications in both academic and real-world contexts.

