Introduction to solving patterns in T-tables and equations
Topic Notes
In this lesson, we will learn:
- How to determine and write one-step and two-step relationships in T-tables as equations with variables
- How to solve equations: isolating variables in two-step relationships (opposite operation to both sides)
Notes:
- Recall that T-tables keep track of patterns and allow calculation of subsequent terms
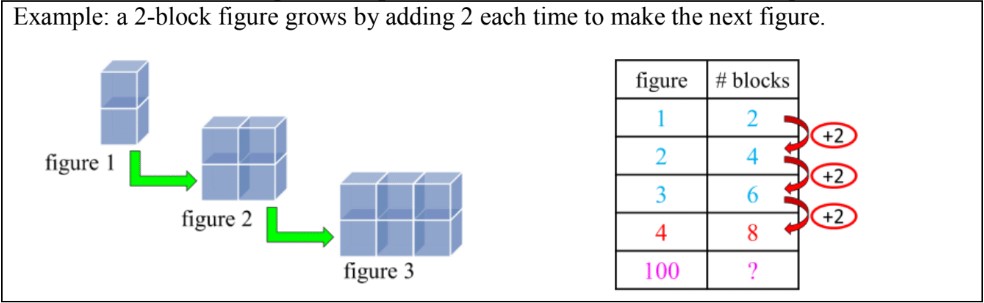
- What is a fast way to find the 100th term? Adding by 2 each time is not efficient.
- T-table columns have a relationship between them. By writing this relationship as an equation, you can put in any number and find information about that term quickly.
- Ask: how do you go from the left column to the right column?
- Find one-step relationships through trial and error (if numbers are getting bigger it is + or ×; if numbers are getting smaller it is - or ÷)
- Assign variables to each column and use these variables in your equation

- For more complicated patterns (two-step relationships) the equation will have two operations: the first step will be [× or ÷] and then the second step will be [+ or -]
- Similar to one-step relationships, they can be found through trial and error
- Isolating variables in two-step equations by “doing the opposite to both sides” in the backwards order of operations (solve by doing + or - first and then × or ÷ after)
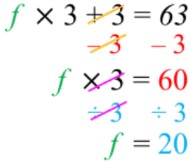
Introduction to Solving Patterns in T-Tables and Equations
Welcome to our lesson on identifying and solving patterns in equations. We'll begin with an introduction video that sets the stage for this crucial mathematical concept. T-tables and equations are fundamental tools in mathematics, and understanding how to recognize and manipulate patterns within them is essential for advancing your problem-solving skills. This lesson will guide you through the process of analyzing t-tables, identifying recurring patterns, and translating these observations into equations. You'll learn how to spot relationships between variables, predict future values, and express these patterns algebraically. By mastering these skills, you'll be better equipped to tackle more complex mathematical challenges in the future. The ability to work with t-tables and equations is not just about solving specific problems; it's about developing a logical approach to mathematical thinking that will serve you well in various academic and real-world scenarios.
Understanding T-Tables and Their Patterns
T-tables are powerful tools used in mathematics to visualize and analyze patterns in sequences. These simple yet effective tables help students and mathematicians alike to identify number rules and predict subsequent terms in a sequence. By organizing data in a clear, two-column format, t-tables make it easier to spot trends and relationships between numbers.
Let's explore how t-tables work using the building blocks example from the video. Imagine a sequence where we're adding building blocks to create a growing structure. The t-table would have two columns: one for the term number (n) and another for the number of blocks (y).
Here's a step-by-step guide to creating and interpreting a t-table using the building blocks example:
- Draw a table with two columns, labeling the left column "n" (for term number) and the right column "y" (for number of blocks).
- Start with the first term (n=1) and record the corresponding number of blocks (y).
- Continue filling in the table for subsequent terms, noting how the number of blocks changes.
- Observe the pattern in the "y" column as "n" increases.
- Look for a relationship between "n" and "y" to identify the number rule.
For example, if we start with 3 blocks and add 2 blocks each time, our t-table might look like this:
- n=1, y=3
- n=2, y=5
- n=3, y=7
- n=4, y=9
By examining this t-table, we can quickly identify the pattern: the number of blocks increases by 2 each time. The number rule can be expressed as y = 2n + 1, where n is the term number.
T-tables are particularly useful for showing patterns because they provide a visual representation of how values change from one term to the next. This makes it easier to spot linear relationships, quadratic, or other types of relationships between variables. In our building blocks example, the linear relationship is clear: for each increase in n, y increases by a constant amount (2).
When using t-tables to identify number rules and find the next term in a sequence, follow these steps:
- Examine the difference between consecutive y-values.
- Determine if the difference is constant (linear) or changing (non-linear).
- If linear, use the constant difference and the initial value to form an equation.
- If non-linear, look for patterns in how the difference changes.
- Once you've identified the rule, use it to predict the next term or any future term in the sequence.
T-tables help students develop pattern recognition skills, which are crucial in mathematics and many other fields. By practicing with t-tables, learners can improve their ability to analyze data, make predictions, and understand functional relationships. This skill is valuable not only in algebra and higher mathematics but also in real-world applications such as finance, science, and data analysis.
In conclusion, t-tables are invaluable tools for visualizing and understanding patterns in sequences. By organizing data systematically, they allow us to easily identify number rules and predict future terms. Whether you're working with simple linear relationships or more complex sequences, mastering the use of t-tables will enhance your mathematical problem-solving skills and deepen your understanding of numerical relationships.
Identifying Relationships Between Columns in T-Tables
T-tables are powerful tools for organizing and analyzing numerical data, but their true potential lies in understanding the relationships between columns in t-tables, not just within them. While it's common to focus on patterns within a single column, recognizing how columns interact with each other can unlock deeper insights and problem-solving abilities.
To find the relationships between columns in t-tables, we need to examine how the values in one column correspond to those in the other. This process involves looking for consistent patterns or operations that connect the two sets of numbers. One effective approach is to use variables to represent unknown numbers in each column, which can help us identify the underlying mathematical relationship.
Let's consider an example t-table:
| Column A | Column B |
|---|---|
| 2 | 6 |
| 3 | 9 |
| 4 | 12 |
| 5 | 15 |
To determine if the relationship is addition, subtraction, multiplication, or division, we can use variables like 'x' for Column A and 'y' for Column B. Then, we can test different operations:
- Addition: Is y = x + a constant?
- Subtraction: Is y = x - a constant?
- Multiplication: Is y = x × a constant?
- Division: Is y = x ÷ a constant?
In our example, we can see that y = 3x for each pair of values. This indicates a multiplication relationship where Column B is always three times Column A.
Here are some more examples of column relationships:
- Addition: If Column A is (1, 2, 3, 4) and Column B is (5, 6, 7, 8), the relationship is y = x + 4.
- Subtraction: If Column A is (10, 15, 20, 25) and Column B is (5, 10, 15, 20), the relationship is y = x - 5.
- Division: If Column A is (12, 18, 24, 30) and Column B is (4, 6, 8, 10), the relationship is y = x ÷ 3.
Understanding these relationships is crucial for predicting unknown values, solving word problems, and recognizing patterns in real-world data. It's a fundamental skill in algebra and data analysis.
To practice identifying column relationships, try these problems:
- Column A: (2, 4, 6, 8), Column B: (4, 8, 12, 16)
- Column A: (10, 20, 30, 40), Column B: (5, 15, 25, 35)
- Column A: (1, 2, 3, 4), Column B: (1, 4, 9, 16)
For each problem, determine the relationship between Column A and Column B. Is it addition, subtraction, multiplication, or division? Or is it a more complex relationship?
Remember, not all relationships will be simple arithmetic operations. Some might involve exponents, square roots, or even combinations of operations. The key is to approach each t-table with an open mind and systematically test different possibilities until you find the consistent relationship that applies to all pairs of values.
By mastering the skill of identifying relationships between columns in t-tables, you'll be better equipped to analyze data, solve complex problems, and understand the underlying patterns in
One-Step Relationships in T-Tables
One-step relationships in t-tables are fundamental concepts in mathematics that involve a single operation between two sets of numbers. These relationships are crucial for understanding basic algebraic concepts and developing problem-solving skills. In this section, we'll explore what one-step relationships are, how to identify them, and provide examples using various operations.
A one-step relationship in a t-table is characterized by a single mathematical operation that connects the input values (usually in the left column) to the output values (in the right column). The four basic operations that can create one-step relationships are addition, subtraction, multiplication, and division.
To identify if a relationship is one-step, examine the pattern between the input and output values. If you can describe the relationship using a single operation that consistently applies to all pairs of numbers, it's likely a one-step relationship. Let's look at some examples:
- Addition: Input + 3 = Output
- Subtraction: Input - 5 = Output
- Multiplication: Input × 2 = Output
- Division: Input ÷ 4 = Output
The trial and error method is an effective approach for finding one-step relationships in t-tables. This method involves testing different operations until you find the one that consistently works for all pairs of numbers in the table. Here's how to apply the trial and error method:
- Start with the first pair of numbers in the t-table.
- Try each of the four basic operations to see which one relates the input to the output.
- Once you find a potential relationship, test it with the other pairs in the table.
- If the relationship works for all pairs, you've found the one-step relationship.
- If not, continue trying other operations or combinations until you find the correct one.
Let's practice identifying one-step relationships with some examples:
Example 1:
| Input | Output |
|---|---|
| 2 | 7 |
| 5 | 10 |
| 8 | 13 |
In this example, the one-step relationship is addition: Input + 5 = Output
Example 2:
| Input | Output |
|---|---|
| 10 | 5 |
| 14 | 7 |
| 22 | 11 |
Here, the one-step relationship is division: Input ÷ 2 = Output
Now, let's try some practice problems. Identify the one-step relationship in each of the following t-tables:
Problem 1:
| Input | Output |
|---|---|
| 3 | 9 |
| 5 | 15 |
| 7 | 21 |
Problem 2:
| Input | Output |
|---|---|
| 12 | 8 |
| 15 | 11 |
| 20 | 16 |
Problem 3:
| Input | Output |
|---|---|
| 3 | 9 |
| 5 | 15 |
| 7 | 21 |
Two-Step Relationships in T-Tables
Two-step relationships in t-tables represent a more complex form of mathematical connection between input and output values. These relationships involve two distinct operations, typically a combination of multiplication or division followed by addition or subtraction. Understanding and identifying these relationships is crucial for problem-solving and developing analytical skills in mathematics.
In a two-step relationship, the input value undergoes two separate transformations before reaching the output value. This process adds an extra layer of complexity compared to single-step relationships, requiring a more nuanced approach to problem-solving. The concept of order of operations plays a vital role in correctly interpreting and solving two-step relationships.
To identify a two-step relationship using the trial and error method, one must carefully analyze the given data and test various combinations of operations. Let's walk through a detailed example to illustrate this process:
Suppose we have the following t-table:
- Input: 2, Output: 7
- Input: 3, Output: 9
- Input: 4, Output: 11
- Input: 5, Output: 13
To identify the two-step relationship, we start by examining the pattern between input and output values. We notice that as the input increases by 1, the output increases by 2. However, this alone doesn't explain the relationship fully.
We can begin our trial and error process by testing different combinations of operations. Let's start with multiplication followed by addition:
- Multiply the input by 2: 2 × 2 = 4, 3 × 2 = 6, 4 × 2 = 8, 5 × 2 = 10
- Add 3 to the result: 4 + 3 = 7, 6 + 3 = 9, 8 + 3 = 11, 10 + 3 = 13
We've successfully identified the two-step relationship: multiply the input by 2, then add 3. This can be expressed as the formula: output = (input × 2) + 3.
The order of operations is crucial in two-step relationships. In our example, if we were to add 3 first and then multiply by 2, we would get incorrect results. Always remember the PEMDAS rule (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) when working with two-step relationships.
Problem-solving in two-step relationships often involves working backwards from the output to the input. For instance, if we're given an output value and asked to find the corresponding input, we would first subtract 3 from the output, then divide the result by 2.
Mastering two-step relationships enhances one's ability to recognize patterns, think critically, and solve complex mathematical problems. It forms a foundation for understanding more advanced mathematical concepts and real-world applications in fields such as physics, engineering, and economics.
In conclusion, two-step relationships in t-tables represent an important concept in mathematical problem-solving. By understanding the process of identifying these relationships through trial and error, and recognizing the importance of order of operations, students can develop stronger analytical skills and a deeper appreciation for the interconnectedness of mathematical operations.
Creating Equations from T-Table Relationships
Understanding how to transform t-table relationships into equations is a crucial skill in mathematics. This process involves recognizing patterns and using variables to represent unknown values, allowing us to express mathematical relationships in a concise and powerful way. Let's explore how to turn t-tables into equations and why this skill is so important.
To begin, we need to understand the role of variables in equations. Variables are symbols, usually letters, that represent unknown numbers or quantities that can change. When we use variables in equations, we're creating a general rule that can apply to many different situations, not just the specific examples in our t-table.
Let's start with one-step relationships. These are the simplest type of equations we can create from t-tables. For example, consider this t-table:
| x | y |
|---|---|
| 1 | 3 |
| 2 | 6 |
| 3 | 9 |
Looking at this table, we can see that y is always 3 times x. We can express this as the equation: y = 3x. This is a one-step equation because it involves only one operation (multiplication) to get from x to y.
Now, let's look at two-step relationships. These involve two operations to get from the input to the output. Consider this t-table:
| x | y |
|---|---|
| 1 | 5 |
| 2 | 7 |
| 3 | 9 |
In this case, we can see that y is always 2 more than twice x. We can express this as the equation: y = 2x + 2. This is a two-step equation because it involves two operations: first multiplying x by 2, then adding 2.
The importance of using variables in these equations cannot be overstated. By using x and y, we create a general rule that works for any value of x, not just the ones in our table. This allows us to make predictions, solve problems, and understand the underlying relationship between the two quantities.
Now, let's practice creating equations from t-tables. Try to write equations for these relationships:
-
x y 2 8 3 12 4 16 -
x y 1 4 2 7 3 10
For the first table, you should notice that y is always 4 times x. The equation is y = 4x. For the second table, y is always 3 more than 3 times x. The equation is y = 3x + 3.
By practicing these skills, you'll become more proficient at recognizing patterns and expressing them as equations. This ability is fundamental in algebra and higher mathematics, allowing you to model real-world situations, solve complex problems, and understand the relationships between different quantities. Remember, the key is to look for the pattern, identify how the output relates to the input, and use variables to express this relationship in a general form.
Solving Equations Derived from T-Tables
Learning to solve equations derived from t-tables is a crucial skill in algebra. This process involves isolating variables and applying opposite operations to both sides of the equation. Let's explore how to tackle both one-step and two-step equations effectively.
Understanding T-Tables and Equation Formation
T-tables are visual tools that help organize information about two related variables. When we derive equations from t-tables, we're essentially creating a mathematical representation of the relationship between these variables. The goal is to solve for one variable in terms of the other.
Solving One-Step Equations
One-step equations are the simplest form of equations we encounter. To solve these, we need to isolate the variable by performing a single operation. The key principle is to do the opposite operation to both sides of the equation. For example:
- If the equation is x + 5 = 12, we subtract 5 from both sides: x = 12 - 5
- If the equation is 3x = 15, we divide both sides by 3: x = 15 ÷ 3
Tackling Two-Step Equations
Two-step equations require two operations to isolate the variable. The process involves:
- First, isolating the term with the variable by using inverse operations
- Then, solving for the variable itself
For example, let's solve 2x + 7 = 15:
- Subtract 7 from both sides: 2x = 15 - 7
- Simplify: 2x = 8
- Divide both sides by 2: x = 8 ÷ 2
- Solve: x = 4
The Concept of Opposite Operations
Opposite operations are fundamental in solving equations. They allow us to undo operations and isolate variables. Remember:
- The opposite of addition is subtraction
- The opposite of multiplication is division
- The opposite of squaring is taking the square root
Always apply the opposite operation to both sides of the equation to maintain balance.
Step-by-Step Example: Solving a Complex Two-Step Equation
Let's solve the equation 3(x - 2) = 21:
- First, distribute the 3: 3x - 6 = 21
- Add 6 to both sides to isolate the term with x: 3x = 27
- Divide both sides by 3: x = 9
Practice Problems
- x + 8 = 13
- 4y = 28
- 2z - 5 = 11
- 5(a + 3) = 40
Conclusion
Mastering the art of solving equations derived from t-tables is essential for success in algebra. Remember to always isolate the variable, use inverse operations, and apply the same operation to both sides of the equation. With practice, you'll become proficient in solving both one-step and two-step equations, paving the way for more advanced mathematical concepts.
Conclusion and Next Steps
In this lesson, we've covered essential concepts for solving linear equations. We began with the introduction video, which laid the groundwork for understanding t-tables and their role in identifying variable relationships. You learned how to create equations from these relationships, a crucial skill in mathematical problem-solving. We then delved into the step-by-step process of solving these equations, applying the principles we discussed. Remember, the ability to interpret t-tables, recognize patterns, and formulate equations is fundamental to many areas of mathematics and real-world applications. As you move forward, practice solving equations regularly to reinforce your understanding. Try creating your own t-tables, deriving equations from various scenarios, and solving them using the methods we've explored. Don't hesitate to revisit the introduction video if you need a refresher on any concepts. With consistent practice, you'll become more confident in your ability to tackle linear equations and related mathematical challenges.
Introduction to Solving Patterns in T-tables and Equations:
Finding one-step relationships between columns in a T-table
Step 1: Understanding T-tables and Patterns
In this lesson, we will be solving patterns in T-tables. First, let's review how T-tables show patterns. T-tables help us keep track of patterns and identify number rules to find the next term. By using a T-table, we can maintain a consistent pattern to find more terms in sequences.
A classic example involves building blocks. Imagine we have figures made of blocks. In the first figure, we have two blocks, in the second figure, we have four blocks, and in the third figure, we have six blocks. We take a snapshot of each step as we build it up. These snapshots are called figures. Between each step, we always add the same number of blocks, creating a pattern.
Step 2: Creating a T-table
To illustrate this pattern, we can create a T-table. The first column represents the figure number, and the second column represents the number of blocks. For example:
- Figure 1: 2 blocks
- Figure 2: 4 blocks
- Figure 3: 6 blocks
By examining the second column, we see the pattern: 2, 4, 6. We are adding 2 blocks each time. Therefore, the number rule is to start at 2 and add 2 for each subsequent figure.
Step 3: Extending the Pattern
Using the pattern, we can predict the number of blocks in future figures. For instance, the fourth figure will have 8 blocks because we add 2 to the number of blocks in the third figure (6 + 2 = 8).
Now, consider a more challenging question: How many blocks are in the 100th figure? Instead of drawing out each figure, we can use the pattern to find the answer more efficiently.
Step 4: Finding Relationships Between Columns
T-tables not only show patterns within columns but also relationships between columns. To find the relationship between the figure number (first column) and the number of blocks (second column), we need to identify a consistent rule.
Let's assign variables to each column: F for the figure number and B for the number of blocks. We need to determine how to go from F to B. By examining the pattern, we see that multiplying the figure number by 2 gives us the number of blocks. For example:
- Figure 1: 1 * 2 = 2 blocks
- Figure 2: 2 * 2 = 4 blocks
- Figure 3: 3 * 2 = 6 blocks
Therefore, the relationship between the columns can be expressed as an equation: F * 2 = B.
Step 5: Using the Equation
With the equation F * 2 = B, we can find the number of blocks for any figure number. For example, to find the number of blocks in the 100th figure, we substitute F with 100:
100 * 2 = 200 blocks
Thus, the 100th figure has 200 blocks.
Step 6: Solving for Different Variables
The equation F * 2 = B can also be used to find the figure number if we know the number of blocks. For example, if there are 86 blocks, we can find the figure number by solving the equation:
F * 2 = 86
To isolate F, we divide both sides by 2:
F = 86 / 2 = 43
Therefore, the 43rd figure has 86 blocks.
Step 7: Applying the Method
This method of finding relationships between columns in a T-table and expressing them as equations is very useful. It allows us to quickly find missing values in the table without having to manually extend the pattern. By understanding and applying these relationships, we can solve a wide range of problems involving patterns in T-tables and equations.
FAQs
1. What is a t-table and how is it used in mathematics?
A t-table is a two-column table used to organize and visualize relationships between two variables. In mathematics, it's primarily used to identify patterns, analyze sequences, and derive equations. The left column typically represents the input (often denoted as 'x'), while the right column shows the corresponding output ('y'). T-tables help students recognize linear, quadratic, or other types of relationships between variables, making them invaluable tools for problem-solving and pattern recognition.
2. How do I identify a one-step relationship in a t-table?
To identify a one-step relationship in a t-table, look for a single consistent operation that connects the input to the output values. This could be addition, subtraction, multiplication, or division. For example, if every output is 3 more than its corresponding input, the relationship is y = x + 3. Use trial and error to test different operations until you find one that works for all pairs in the table.
3. What's the difference between one-step and two-step relationships in t-tables?
One-step relationships involve a single operation (like addition or multiplication) to get from the input to the output. Two-step relationships require two distinct operations, typically a combination of multiplication/division followed by addition/subtraction. For example, y = 2x + 3 is a two-step relationship where you first multiply the input by 2, then add 3.
4. How do I create an equation from a t-table relationship?
To create an equation from a t-table, first identify the pattern between input (x) and output (y) values. Use variables to represent this relationship. For a one-step relationship like y = 3x, you'd recognize that each y-value is 3 times its corresponding x-value. For two-step relationships, identify both operations involved. Always verify your equation works for all pairs in the table.
5. Why is understanding t-tables and equations important in mathematics?
Understanding t-tables and equations is crucial because it develops critical thinking and pattern recognition skills. These concepts form the foundation for more advanced mathematical topics like algebra, calculus, and data analysis. They also have practical applications in fields such as physics, economics, and engineering, where relationships between variables need to be understood and quantified. Mastering these skills enhances problem-solving abilities and prepares students for more complex mathematical challenges.
Prerequisite Topics
Understanding the foundation of mathematics is crucial when delving into more complex topics like "Introduction to solving patterns in T-tables and equations." To excel in this area, it's essential to have a solid grasp of several key concepts.
First and foremost, a strong understanding of linear relationships is vital. These relationships form the backbone of many mathematical patterns and equations you'll encounter. By mastering this concept, you'll be better equipped to recognize and interpret the patterns that emerge in T-tables and equations.
Equally important is the skill of identifying variable relationships. This ability allows you to discern how different variables interact within an equation or T-table, which is crucial for solving patterns effectively.
When working with T-tables, you'll often need to translate the information into equations. This is where creating equations from t-tables comes into play. Understanding how to graph linear functions using various forms, particularly the slope-intercept form (y=mx+b), will greatly enhance your ability to visualize and solve patterns.
One cannot overstate the importance of mastering the order of operations PEMDAS. This fundamental concept is the key to solving equations correctly and consistently. Without a solid grasp of PEMDAS, you may find yourself making errors when solving complex patterns in T-tables and equations.
Lastly, the skill of expressing patterns algebraically is crucial. This involves translating visual or numerical patterns into algebraic expressions or inequalities. By mastering this skill, you'll be able to represent and manipulate patterns more effectively, leading to more efficient problem-solving.
Each of these prerequisite topics builds upon one another, creating a strong foundation for tackling more advanced concepts. By investing time in understanding these fundamental areas, you'll find that solving patterns in T-tables and equations becomes more intuitive and manageable. Remember, mathematics is a cumulative subject, and a solid grasp of these prerequisites will not only help you in this specific topic but will also serve you well throughout your mathematical journey.

