Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Introduction to Line Symmetry
Welcome to our exploration of line symmetry, also known as reflection symmetry! This fascinating concept is all around us in nature and design. Imagine folding a shape in half and having both sides match perfectly - that's line symmetry in action. Our introduction video is a great starting point to visualize this concept. It demonstrates how objects can be divided by a line, creating mirror images on either side. This video is crucial in laying the foundation for understanding more complex symmetrical patterns. As we delve deeper, you'll discover how line symmetry applies to various shapes and real-world objects. From butterflies to buildings, symmetry plays a significant role in our world. By mastering this concept, you'll enhance your spatial reasoning skills and gain a new appreciation for geometric patterns. Let's embark on this symmetrical journey together, and soon you'll be spotting line symmetry everywhere you look!
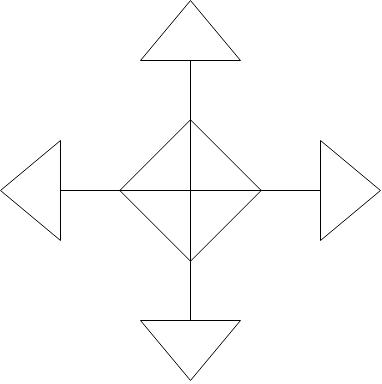
Find and draw all the lines of symmetry for each figure.

Step 1: Understanding Line Symmetry
Line symmetry, also known as reflection symmetry, occurs when a figure can be divided into two identical halves that are mirror images of each other. The line that divides the figure is called the line of symmetry. There are different types of lines of symmetry, including vertical, horizontal, and oblique (diagonal) lines. In this task, we will identify and draw all the lines of symmetry for the given figures.
Step 2: Identifying Vertical Lines of Symmetry
First, let's look for vertical lines of symmetry. A vertical line of symmetry divides the figure into two identical halves along a vertical axis. For the given figures, observe if drawing a vertical line through the center of the figure results in two mirror-image halves. If it does, then that line is a vertical line of symmetry.
Step 3: Identifying Horizontal Lines of Symmetry
Next, we need to check for horizontal lines of symmetry. A horizontal line of symmetry divides the figure into two identical halves along a horizontal axis. For the given figures, observe if drawing a horizontal line through the center of the figure results in two mirror-image halves. If it does, then that line is a horizontal line of symmetry.
Step 4: Identifying Oblique Lines of Symmetry
Finally, we need to check for oblique (diagonal) lines of symmetry. An oblique line of symmetry divides the figure into two identical halves along a diagonal axis. For the given figures, observe if drawing a diagonal line through the center of the figure results in two mirror-image halves. If it does, then that line is an oblique line of symmetry.
Step 5: Drawing the Lines of Symmetry
Once we have identified the lines of symmetry, the next step is to draw them on the figures. Use a ruler to draw straight lines through the center of the figures along the identified axes. Ensure that the lines are accurately placed to reflect the symmetry of the figures.
Step 6: Verifying the Symmetry
After drawing the lines of symmetry, verify that each line correctly divides the figure into two identical halves. Fold the figure along the drawn lines (mentally or physically) to check if the two halves match perfectly. If they do, the lines are correctly identified as lines of symmetry.
Step 7: Conclusion
In conclusion, identifying and drawing lines of symmetry involves understanding the concept of reflection symmetry and carefully observing the figures to find vertical, horizontal, and oblique lines that divide the figures into identical halves. By following the steps outlined above, you can accurately find and draw all the lines of symmetry for any given figure.
-
What is the difference between line symmetry and rotational symmetry?
Line symmetry, also known as reflection symmetry, occurs when a shape can be divided into two identical halves by a line. Rotational symmetry, on the other hand, is when a shape looks the same after being rotated around a central point. For example, a rectangle has line symmetry, while a square has both line and rotational symmetry.
-
How do you determine the order of rotational symmetry?
To determine the order of rotational symmetry, rotate the shape around its center point and count how many times it appears identical to its starting position during a complete 360-degree rotation. For instance, an equilateral triangle has an order of rotational symmetry of 3, as it looks the same three times during a full rotation.
-
Can a shape have both line symmetry and rotational symmetry?
Yes, many shapes can have both line and rotational symmetry. A square is a perfect example, having four lines of symmetry (two diagonal and two through the midpoints of opposite sides) and rotational symmetry of order 4. Regular polygons generally possess both types of symmetry.
-
What is the significance of symmetry in nature and design?
Symmetry is prevalent in nature and widely used in design due to its aesthetic appeal and functional benefits. In nature, symmetry often indicates genetic health and efficiency. In design and architecture, symmetry creates balance, harmony, and visual appeal. It's also crucial in fields like physics and chemistry for understanding molecular structures and physical laws.
-
How is the angle of rotational symmetry calculated?
The angle of rotational symmetry is calculated by dividing 360 degrees by the order of rotational symmetry. For example, if a shape has rotational symmetry of order 5 (like a regular pentagon), the angle of rotational symmetry would be 360° ÷ 5 = 72°. This means the shape looks identical every 72 degrees of rotation.
Understanding line symmetry is a fundamental concept in geometry that builds upon several basic mathematical principles. While there are no specific prerequisite topics listed for this subject, it's important to recognize that a strong foundation in general mathematical concepts can greatly enhance your comprehension of line symmetry.
Line symmetry, also known as reflection symmetry, is a concept that appears in various aspects of mathematics and everyday life. It involves the idea that a shape or object can be divided into two identical halves by a line, called the line of symmetry. To fully grasp this concept, students should have a solid understanding of basic geometric shapes, spatial awareness, and the ability to visualize transformations.
Although not explicitly listed as prerequisites, familiarity with concepts such as points, lines, and planes can be beneficial when studying line symmetry. These fundamental geometric elements form the basis for understanding how shapes can be reflected across a line. Additionally, a basic grasp of coordinate geometry can be helpful when working with line symmetry in a coordinate plane.
Another important aspect that contributes to understanding line symmetry is the ability to recognize patterns and relationships between shapes. This skill is developed through various mathematical experiences and can be enhanced by practicing with puzzles, tangrams, and other visual-spatial activities.
While not a direct prerequisite, having a basic understanding of fractions and proportions can also be advantageous when exploring line symmetry. These concepts can help students appreciate the equal distribution of parts on either side of the line of symmetry and understand how symmetrical shapes maintain their proportions.
It's worth noting that many of these foundational skills are developed naturally through a well-rounded mathematics education. As students progress through their mathematical journey, they build upon previous knowledge, creating a strong framework for understanding more complex concepts like line symmetry.
Even though there are no specific prerequisites listed for line symmetry, it's crucial for students to approach the topic with an open mind and a willingness to connect it to their existing mathematical knowledge. Teachers and educators can help by drawing connections between line symmetry and previously learned concepts, making the learning process more intuitive and engaging.
In conclusion, while line symmetry doesn't have explicit prerequisites, a strong foundation in basic geometry, spatial reasoning, and pattern recognition can significantly enhance a student's ability to grasp and apply this concept. By building upon their existing mathematical knowledge and experiences, students can develop a deeper appreciation for the beauty and practicality of line symmetry in both mathematics and the world around them.