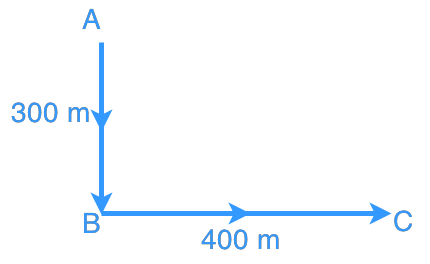
- An aeroplane flew from point A to point B, and then to Point C. How far is the plane from point A? Refer to the diagram below.
- A 2.5 m long ladder is put against a wall. If the base of the ladder is 1.25 m away from the wall, what is the length from the ground to the point where the top of ladder touches the wall?
- Which triangle has a longer perimeter?
Triangle A
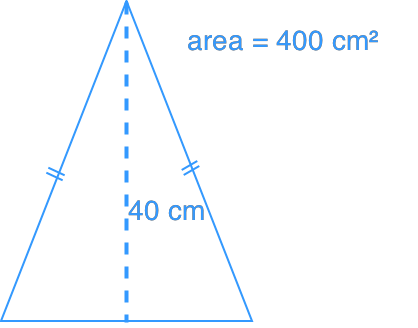 Triangle B
Triangle B
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Introduction to Applying the Pythagorean Theorem
Welcome to our exploration of the Pythagorean theorem and its real-world applications! This fundamental principle in geometry states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of squares of the other two sides. As we dive into applying the Pythagorean theorem, you'll discover its incredible versatility. From calculating distances and heights to solving complex engineering problems, this theorem is a powerful tool in mathematics and beyond. Our introduction video will guide you through the basics, making it easier to grasp this essential concept. You'll see how the Pythagorean theorem comes to life in architecture, navigation, and even in your smartphone's GPS! Understanding the applications of the Pythagorean theorem will not only boost your math skills but also help you appreciate its significance in everyday scenarios. Let's embark on this exciting journey to uncover the practical uses of this ancient yet timeless mathematical principle!
-
How is the Pythagorean theorem applied?
The Pythagorean theorem is applied in various fields, including architecture, engineering, and navigation. It's used to calculate unknown lengths in right triangles, determine distances between points, and verify if angles are right angles. In construction, it helps ensure walls are perpendicular and in calculating roof slopes. In navigation, it's crucial for determining the shortest route between two points.
-
How do I solve using the Pythagorean theorem?
To solve using the Pythagorean theorem, follow these steps: 1. Identify the right triangle in the problem. 2. Label the sides: a and b for the two shorter sides, c for the hypotenuse. 3. Use the formula a² + b² = c². 4. Plug in the known values and solve for the unknown side. For example, if a = 3 and b = 4, then 3² + 4² = c², so c = (9 + 16) = 25 = 5.
-
What are 3 different real-life uses of the Pythagorean theorem?
1. Architecture: Calculating roof slopes and ensuring walls are perpendicular. 2. Navigation: Determining the shortest distance between two points for GPS and flight paths. 3. Sports: Measuring field dimensions and calculating trajectories in games like baseball or golf.
-
What is the Pythagorean theorem only used on?
The Pythagorean theorem is specifically used on right triangles, where one angle is 90 degrees. It establishes the relationship between the lengths of the three sides in these triangles. While it's most directly applicable to right triangles, its principles can be extended to solve problems involving any shape that can be broken down into right triangles.
-
How can the Pythagorean theorem be applied in everyday situations?
In everyday life, the Pythagorean theorem can be applied in various situations: 1. Home improvement: Measuring diagonal distances for flooring or wallpaper. 2. Technology: Calculating screen sizes of TVs and monitors. 3. Outdoor activities: Determining distances in hiking or planning garden layouts. 4. DIY projects: Ensuring furniture or structures are square and level. These applications demonstrate how this ancient mathematical principle remains relevant in modern daily life.
Understanding the Applications of the Pythagorean Theorem requires a solid foundation in basic mathematical concepts. While there are no specific prerequisite topics provided for this subject, it's important to recognize that a strong grasp of fundamental geometry and algebra is essential for fully appreciating and applying this powerful mathematical tool.
The Pythagorean Theorem, a cornerstone of geometry, has numerous practical applications in various fields. To effectively utilize this theorem, students should be comfortable with basic geometric principles, including the properties of triangles, particularly right triangles. A clear understanding of square roots and exponents is also crucial, as these concepts are integral to the theorem's formula.
Additionally, familiarity with algebraic equations and problem-solving techniques is beneficial when working with the Pythagorean Theorem. This knowledge allows students to manipulate the theorem's equation (a² + b² = c²) to solve for unknown side lengths in right triangles.
While not explicitly listed as prerequisites, topics such as coordinate geometry and trigonometry often intersect with applications of the Pythagorean Theorem. For instance, calculating distances between points in a coordinate plane or understanding the relationship between the theorem and trigonometric functions can enhance one's ability to apply the concept in diverse scenarios.
Real-world applications of the Pythagorean Theorem span various disciplines, including architecture, engineering, and navigation. Students with a solid understanding of measurement units and scale will find it easier to relate the theorem to practical situations, such as determining the length of a ladder needed to reach a certain height or calculating the diagonal of a rectangular room.
Moreover, basic problem-solving skills and logical thinking are invaluable when approaching applications of the Pythagorean Theorem. The ability to visualize spatial relationships and translate word problems into mathematical equations is crucial for successfully applying the theorem in both academic and real-world contexts.
As students delve into the applications of the Pythagorean Theorem, they may find that revisiting fundamental concepts in geometry and algebra strengthens their overall understanding. This reinforcement not only aids in mastering the theorem itself but also builds a robust foundation for more advanced mathematical topics.
In conclusion, while specific prerequisites are not listed, a strong background in basic geometry, algebra, and problem-solving skills is essential for fully grasping and applying the Pythagorean Theorem. By ensuring a solid understanding of these foundational concepts, students will be well-equipped to explore the diverse and fascinating applications of this timeless mathematical principle.



