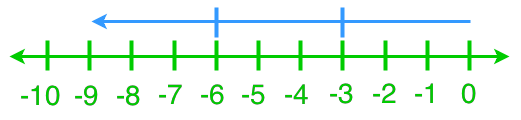
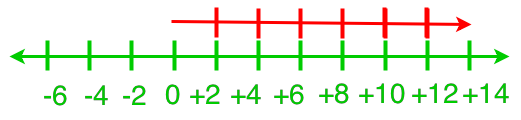In this lesson, we will learn:
- Understanding Division Using a Number Line
- Solving Division Statements Using a Number Line
- Division Statements With Integer Quotients
- Division Statements With Non-Integer Quotients
- Word Problems of Dividing Integers
Notes:
- Recurring/ repeating decimals: decimal numbers whose digits repeat forever.
- For the recurring decimals, we put either a bar or dots above the recurring parts.