Number patterns

In this lesson, we will learn:

• How to find the rule for a number sequence and write an expression for it
• How to predict the next term in a number sequence

Notes:

• Number patterns can also be called number sequences
• A number sequence is a list of numbers (or terms) in order
• The order of number is decided by a mathematical rule
• The same operation (+, –, ×, ÷) is used between each term.


• An expression can be written for any number pattern/sequence
• The expression states what the first number in the list is, and what the rule is
• “start at _[#]_ and _[operation]_by_[#]_ each time.”
• For example,

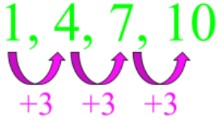
• The rule is to add 3 and the expression is to “start at 1 and add by 3 each time”

• If a rule for a number pattern/sequence is known, you can predict the next terms
• Using the previous example,

• The next two terms in the sequence are 13 and 16

• Always find the rule by using two consecutive numbers (right next to each other) in the sequence
• For example,

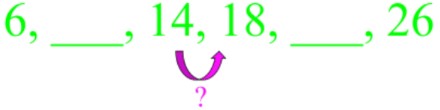
• The rule is to add 4, therefore the entire sequence should be completed as: 6, 10, 14, 18, 22, 26