Operations with metric units
Topic Notes
In this lesson, we will learn:
- Adding mixed metric units
- Subtracting mixed metric units
Notes:
Metric Units of Length:
1km = 1000 m
1 m = 100 cm
1 cm = 10 mm
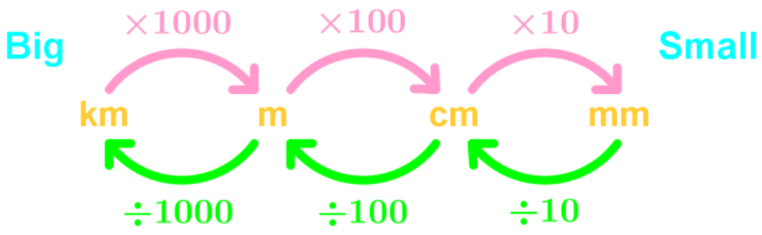
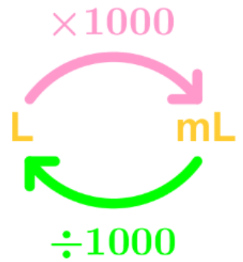
Metric Units of Volume
1L = 1000 mL
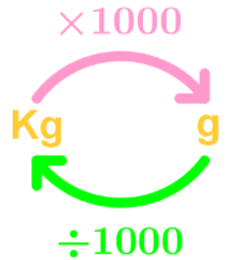
Metric Units of Weight
1kg = 1000 g
-to add or subtract measurements measurements must be in the SAME units
Adding Mixed Metric Units Steps
- Group together like units
- Add like units (starting with smaller units)
- Rename and Regroup units (if you need to)
Subtracting Metric Units Steps
- Group together like units
- Rename and regroup units (if you need to)
- Subtract like units
Introduction to Operations with Metric Units
Welcome to our exploration of operations with metric units! This fundamental topic is crucial for understanding measurement in science, engineering, and everyday life. Our introduction video serves as an excellent starting point, providing a clear and engaging overview of the metric system and how to perform basic operations with these units. As your math tutor, I'm excited to guide you through this journey. We'll cover everything from simple conversions to more complex calculations involving metric units. The video will help you visualize these concepts, making them easier to grasp and remember. Remember, mastering metric units is like learning a new language it opens up a world of possibilities in mathematics and beyond. So, let's dive in and discover how these units work together. With practice, you'll soon be confidently handling metric measurements in various real-world scenarios.
Adding and Subtracting Metric Units with Same Units
When it comes to working with metric units, one of the most fundamental operations is adding and subtracting measurements. However, it's crucial to remember that these operations can only be performed when the units are the same. Let's dive into this concept and explore how to add and subtract metric units correctly.
First and foremost, the golden rule: you can only add or subtract measurements that have the same units. For instance, you can add meters to meters, or subtract grams from grams, but you cannot add meters to grams. This principle is essential for maintaining the accuracy and meaning of your calculations.
Let's take a simple example: 8 meters + 3 meters. In this case, both measurements are in meters, so we can proceed with the addition. The process is straightforward:
- Identify the units (meters in this case)
- Ensure both measurements have the same units
- Perform the addition: 8 + 3 = 11
- Keep the original unit (meters) in the result
So, 8 meters + 3 meters = 11 meters. The same principle applies to subtraction. For example, 15 kilometers - 7 kilometers = 8 kilometers.
Here's a step-by-step guide for adding or subtracting metric units:
- Check the units of all measurements involved
- Confirm that all units are the same
- If units differ, convert them to the same unit before proceeding
- Perform the addition or subtraction as you would with regular numbers
- Write the result with the common unit
It's important to note that if you encounter measurements with different units, you must convert them to the same unit before adding or subtracting. For example, you can't directly add 5 meters to 20 centimeters. You would first need to convert either the meters to centimeters or the centimeters to meters.
Remember, this principle applies to all metric units, not just length measurements. Whether you're working with volume (liters, milliliters), mass (grams, kilograms), or any other metric quantity, always ensure you're dealing with the same units before performing addition or subtraction.
By following these guidelines, you'll ensure accurate calculations and avoid common mistakes when working with metric units. Practice with various examples to become comfortable with this concept, and you'll find that adding and subtracting metric units becomes second nature in no time!
Converting Units for Addition and Subtraction
When working with metric units, it's crucial to understand the importance of converting different units, especially when adding or subtracting quantities with different units. This concept is fundamental in mathematics and science, and mastering it will make your calculations much more accurate and meaningful. Let's dive into why unit conversion is necessary and how to do it effectively.
Imagine you're trying to solve a problem like "8 meters + 3 centimeters." At first glance, you might be tempted to simply add the numbers together and get 11. However, this would be incorrect because we're dealing with different units. Meters and centimeters are both units of length, but they represent different scales. One meter is equal to 100 centimeters, so we can't just add them together without converting first.
To properly add or subtract metric units with different units, we need to follow a simple process:
- Choose a common unit to convert to (usually the larger unit)
- Convert all measurements to this common unit
- Perform the addition or subtraction
- Express the final answer in the most appropriate unit
Let's apply this process to our example of "8 meters + 3 centimeters":
- We'll choose meters as our common unit since it's the larger unit in this case.
- We need to convert 3 centimeters to meters. Since 1 meter = 100 centimeters, we divide 3 by 100: 3 ÷ 100 = 0.03 meters.
- Now we can add: 8 meters + 0.03 meters = 8.03 meters.
- Our final answer is 8.03 meters, which is the most appropriate unit for this result.
This process works the same way when subtracting. For example, if we had "10 meters - 50 centimeters," we would convert 50 centimeters to 0.5 meters and then subtract: 10 - 0.5 = 9.5 meters.
Remember, converting different units is not just about getting the right answer; it's about understanding the relationships between different units of measurement. In the metric system, these relationships are based on powers of 10, which makes conversions relatively straightforward once you get the hang of it.
Here's a quick reference for common metric length conversions:
- 1 meter = 100 centimeters
- 1 meter = 1000 millimeters
- 1 centimeter = 10 millimeters
By practicing unit conversions and always being mindful of the units you're working with, you'll become more confident in your ability to solve problems involving different metric units. This skill is invaluable in many fields, including science, engineering, and everyday life situations where precise measurements are important.
So, the next time you encounter a problem with different units, don't panic! Take a deep breath, identify the units involved, choose a common unit, convert as needed, and then perform your calculations. With practice, this process will become second nature, and you'll be handling complex unit conversions with ease.
Working with Mixed Measurements
Hey there! Let's dive into the fascinating world of mixed measurements. You know, those tricky problems where you have to work with different units at the same time? Don't worry, I'm here to guide you through it step by step!
Imagine you're in the kitchen, following a recipe, and you come across measurements like "3 kilograms, 200 grams" or "4 liters, 200 milliliters." These are perfect examples of mixed measurements. They combine larger units (like kilograms or liters) with smaller units (like grams or milliliters) in the same expression. It might seem confusing at first, but I promise you'll get the hang of it!
Let's start with a simple addition problem: "3 kilograms, 200 grams + 2 kilograms, 600 grams." Now, how do we tackle this? The key is to break it down into manageable steps:
1. First, let's group like units together. We have kilograms and grams, so we'll work with each separately.
2. For the kilograms: 3 kg + 2 kg = 5 kg
3. For the grams: 200 g + 600 g = 800 g
4. Now, we combine our results: 5 kg and 800 g
But wait! Remember that 1000 grams make a kilogram. So, we can simplify this further:
5. Convert 800 g to kg: 800 g = 0.8 kg
6. Add this to our kilogram total: 5 kg + 0.8 kg = 5.8 kg
And there you have it! 3 kilograms, 200 grams + 2 kilograms, 600 grams = 5.8 kilograms.
Now, let's try a subtraction problem with liquids: "4 liters, 200 milliliters - 1 liter, 150 milliliters." We'll use the same step-by-step approach:
1. Group like units: liters and milliliters
2. For liters: 4 L - 1 L = 3 L
3. For milliliters: 200 mL - 150 mL = 50 mL
4. Combine results: 3 L and 50 mL
In this case, we don't need to convert milliliters to liters because 50 mL is less than 1 L (1000 mL). So our final answer is 3 liters, 50 milliliters.
The key to mastering mixed measurements is practice and patience. Remember these tips:
- Always group like units together first
- Perform calculations within each unit group
- Combine results, converting smaller units to larger ones when possible
- Double-check your work to avoid simple mistakes
As you work with mixed measurements more often, you'll find it becomes second nature. Whether you're cooking, doing science experiments, or solving math problems, these skills will come in handy. Don't get discouraged if it takes a bit of time to get comfortable with the process. Everyone learns at their own pace!
Mixed measurements are a great way to understand how different units relate to each other. They help us appreciate the flexibility of our measurement systems and how we can express quantities in various ways. Plus, they're super useful in real-life situations. Imagine trying to measure ingredients for a large batch of cookies or calculating the total volume of liquid in different containers. Mixed measurements make these tasks much easier!
Remember, if you ever feel stuck, don't hesitate to ask for help or look up additional examples. There are plenty of resources available to support your learning journey. Keep practicing, and soon you'll be a pro at handling mixed measurements of all kinds!
Addition with Mixed Measurements: A Detailed Example
Welcome to our step-by-step guide on adding mixed measurements! Today, we'll walk you through the process using a practical example: '2 liters, 900 milliliters + 1 liter, 100 milliliters'. This common scenario often arises in cooking, science experiments, or everyday life situations. Don't worry if it seems tricky at first we'll break it down into easy-to-follow steps!
Step 1: Identify and Group Like Units
First, let's organize our measurements by grouping like units together. In our example, we have:
Liters: 2 liters and 1 liter
Milliliters: 900 milliliters and 100 milliliters
This simple step makes the addition process much more manageable.
Step 2: Add the Smaller Units First
We'll start by adding the milliliters:
900 milliliters + 100 milliliters = 1000 milliliters
Great job! We've successfully combined the smaller units.
Step 3: Add the Larger Units
Now, let's add the liters:
2 liters + 1 liter = 3 liters
Excellent progress! We've now added both the smaller and larger units separately.
Step 4: Combine the Results
At this point, we have:
3 liters and 1000 milliliters
We're almost there, but we need one more step to express this in standard form.
Step 5: Rename and Regroup if Necessary
Here's where our knowledge of unit conversion comes in handy. We know that 1000 milliliters equal 1 liter. So, we can convert our 1000 milliliters to 1 liter:
3 liters + 1 liter (from 1000 milliliters) = 4 liters
Congratulations! We've successfully added our mixed measurements and simplified the result.
Final Answer: 2 liters, 900 milliliters + 1 liter, 100 milliliters = 4 liters
Let's recap the key steps in adding mixed measurements: 1. Group like units together 2. Add smaller units first 3. Add larger units 4. Combine the results 5. Rename and regroup if necessary
Remember, the key to success with mixed measurements is to take it step by step. Always start with the smaller units, then move to the larger ones. Don't forget to check if you need to convert any units at the end to simplify your answer.
This method works for various types of measurements, not just volume. You can apply the same principles to length (e.g., meters and centimeters), weight (e.g., kilograms and grams), or any other measurement system with multiple units.
Practice makes perfect! Try creating your own mixed measurement addition problems. Start with simple ones and gradually increase the complexity. You'll find that with each problem you solve, your confidence and speed will improve.
Remember, working with mixed measurements is a valuable skill that extends beyond math class. It's useful in cooking, construction, science experiments, and many other real-world applications. By mastering this skill, you're equipping yourself with practical knowledge that will serve you well in various aspects of life.
If you ever feel stuck, don't hesitate to review these steps or seek help from a teacher or tutor. Math skills, including working with mixed measurements, develop over time with practice and patience. Keep up the great work, and soon you'll be adding mixed measurements with ease!
Subtraction with Mixed Measurements: A Comprehensive Guide
Subtracting mixed measurements can seem daunting at first, but with a systematic approach, it becomes much more manageable. Let's walk through the process using the example '4 meters, 300 centimeters - 2 meters, 400 centimeters'. This guide will help you understand the steps for subtracting mixed measurements, including grouping like units, renaming, and regrouping when necessary.
Step 1: Align like units
First, we need to align the measurements so that like units are in the same column. In our example:
4 meters, 300 centimeters
- 2 meters, 400 centimeters
Step 2: Check if regrouping is necessary
In subtraction, we need to ensure that each part of the top number (minuend) is larger than or equal to the corresponding part of the bottom number (subtrahend). In our case, 300 centimeters is smaller than 400 centimeters, so we need to regroup.
Step 3: Regroup and rename
To regroup, we'll borrow 1 meter from the 4 meters and convert it to centimeters. Remember, 1 meter = 100 centimeters. So our new arrangement looks like this:
3 meters, 1300 centimeters
- 2 meters, 400 centimeters
Step 4: Perform the subtraction
Now that we've regrouped, we can subtract each column:
Meters: 3 - 2 = 1 meter
Centimeters: 1300 - 400 = 900 centimeters
Step 5: Write the final answer
Our result is 1 meter, 900 centimeters.
It's important to note the differences between addition and subtraction of mixed measurements. In addition, we simply add like units and then convert if necessary. In subtraction, we often need to regroup before we can perform the operation, especially when the top number in any unit is smaller than the bottom number.
Remember, patience is key when working with mixed measurements. Take your time to align the units properly and don't hesitate to regroup when needed. It's also helpful to double-check your work by adding the result to the subtrahend it should equal the minuend.
Practice is essential for mastering this skill. Try creating your own mixed measurement subtraction problems, gradually increasing in complexity. Start with simple problems where regrouping isn't necessary, then move on to problems that require borrowing from larger units.
As you become more comfortable with the process, you'll find that subtracting mixed measurements becomes second nature. Don't get discouraged if you make mistakes at first they're a natural part of the learning process. Keep at it, and you'll soon be handling these problems with confidence and ease.
In summary, the key steps for subtracting mixed measurements are:
- Align like units
- Check if regrouping is necessary
- Regroup and rename if needed
- Perform the subtraction
- Write the final answer
By following these steps and practicing regularly, you'll develop a strong foundation in handling mixed measurements. This skill is invaluable in many real-world applications, from construction and engineering to cooking and crafting. Keep practicing, stay patient with yourself, and soon you'll be tackling even the most complex mixed measurement subtractions with ease!
Common Challenges and Tips for Operations with Metric Units
Working with metric units can be tricky for many students, but don't worry! We're here to help you overcome these challenges. One of the most common issues is forgetting to align like units when performing calculations. Remember, you can't add apples and oranges, and the same goes for meters and centimeters! Always make sure you're working with the same unit before adding or subtracting.
Another frequent stumbling block is making errors during unit conversion. It's easy to get confused when moving between different metric prefixes. Here's a helpful tip: think of the metric system as a ladder. Each step up or down the ladder represents a change by a factor of 10. To move up (to a smaller unit), multiply by 10. To move down (to a larger unit), divide by 10.
A great strategy to avoid conversion errors is to use a place value chart. Draw columns for each metric prefix (kilo-, hecto-, deka-, base unit, deci-, centi-, milli-) and practice moving numbers across these columns. This visual aid can really help cement the concept in your mind.
When it comes to remembering the order of metric prefixes, try this mnemonic: "King Henry Died By Drinking Chocolate Milk." Each word represents a prefix in order: Kilo-, Hecto-, Deka-, Base unit, Deci-, Centi-, Milli-. This fun phrase can be a lifesaver during exams!
Don't forget about estimation skills! Before diving into calculations, take a moment to estimate what your answer should roughly be. This can help you catch major errors early on. For example, if you're converting 5 km to m, you know the answer should be larger than 5, not smaller.
Practice is key to mastering metric operations. Try creating your own real-life scenarios with metric units. This not only makes learning more engaging but also helps you understand how these concepts apply in everyday situations.
Lastly, don't be discouraged if you make mistakes. Every error is an opportunity to learn and improve. Keep a "error log" where you note down common mistakes and how to avoid them in the future. This personalized reference can be incredibly valuable as you progress.
Remember, everyone learns at their own pace. With persistence and these strategies, you'll soon find metric operations becoming second nature. Keep up the great work, and don't hesitate to ask for help when needed!
A great strategy to avoid conversion errors is to use a place value chart. Draw columns for each metric prefix (kilo-, hecto-, deka-, base unit, deci-, centi-, milli-) and practice moving numbers across these columns. This visual aid can really help cement the concept in your mind.
Practice is key to mastering metric operations. Try creating your own real-life scenarios with metric units. This not only makes learning more engaging but also helps you understand how these concepts apply in everyday situations.
Conclusion and Practice Recommendations
In conclusion, this comprehensive overview has covered essential aspects of the subject matter. We've explored key concepts, methodologies, and best practices that are crucial for success in this field. Remember to apply these principles consistently in your work. It's important to stay updated with the latest trends and developments, as this area is constantly evolving. Practice regularly to hone your skills and gain practical experience. Don't hesitate to seek feedback from peers or mentors to improve your performance. Networking and collaboration can also provide valuable insights and opportunities. Set realistic goals and track your progress to maintain motivation. Continuous learning and adaptation are vital for long-term success. By implementing these strategies and maintaining a proactive approach, you'll be well-equipped to excel in your endeavors. Stay curious, remain open to new ideas, and always strive for excellence in your practice.
Introduction to Operations with Metric Units
In this guide, we will explore the basics of adding metric units. Understanding how to properly add metric units is essential for solving various mathematical problems involving measurements. Let's dive into the step-by-step process.
Step 1: Understanding the Basics
Before we start adding metric units, it's important to understand the fundamental concept. Metric units are a standard of measurement used globally, and they include units such as meters, centimeters, kilograms, grams, liters, and milliliters. When adding metric units, the units must be the same. For example, you can add meters to meters or grams to grams, but you cannot directly add meters to centimeters without converting one of the units.
Step 2: Simple Addition of Same Units
Let's start with a simple example: adding 8 meters and 3 meters. Since both measurements are in meters, you can directly add them together:
8 meters + 3 meters = 11 meters
This is straightforward because the units are the same. The result is 11 meters.
Step 3: Adding Different Units
Now, let's consider a more complex example: adding 8 meters and 3 centimeters. Since the units are different, you cannot directly add them together. You need to convert one of the units so that both measurements are in the same unit. You can either convert meters to centimeters or centimeters to meters. Heres how you can do it:
1 meter = 100 centimeters
So, 8 meters = 8 * 100 = 800 centimeters
Now, add the converted measurements:
800 centimeters + 3 centimeters = 803 centimeters
Alternatively, you could convert centimeters to meters:
3 centimeters = 3 / 100 = 0.03 meters
Now, add the converted measurements:
8 meters + 0.03 meters = 8.03 meters
Step 4: Working with Mixed Measurements
Sometimes, you may encounter mixed measurements, which include different units within the same measurement. For example, consider the following addition problem:
3 kilograms 200 grams + 2 kilograms 600 grams
To solve this, you need to add the kilograms and grams separately:
3 kilograms + 2 kilograms = 5 kilograms
200 grams + 600 grams = 800 grams
So, the result is 5 kilograms 800 grams.
Step 5: Subtracting Mixed Measurements
Subtraction of mixed measurements follows a similar process. Consider the following example:
4 liters 200 milliliters - 1 liter 150 milliliters
Subtract the liters and milliliters separately:
4 liters - 1 liter = 3 liters
200 milliliters - 150 milliliters = 50 milliliters
So, the result is 3 liters 50 milliliters.
Step 6: Ensuring Consistency in Units
Always ensure that the units are consistent before performing any addition or subtraction. If the units are different, convert them to the same unit. This is crucial for obtaining accurate results.
Step 7: Practice Problems
To reinforce your understanding, practice with the following problems:
1. Add 5 meters and 250 centimeters.
2. Subtract 3 kilograms 500 grams from 7 kilograms 200 grams.
3. Add 2 liters 300 milliliters and 1 liter 750 milliliters.
4. Subtract 6 meters 150 centimeters from 10 meters 50 centimeters.
By practicing these problems, you will become more proficient in adding and subtracting metric units.
FAQs
-
What is the most important rule when adding or subtracting metric units?
The most important rule when adding or subtracting metric units is to ensure that all measurements have the same unit. You can only perform these operations on quantities with identical units. For example, you can add meters to meters or subtract grams from grams, but you cannot add meters to grams.
-
How do you convert between different metric units?
To convert between metric units, remember that each step up or down the metric scale represents a change by a factor of 10. To convert to a smaller unit (e.g., meters to centimeters), multiply by 10 for each step. To convert to a larger unit (e.g., milliliters to liters), divide by 10 for each step. For example, to convert 5 meters to centimeters, multiply by 100 (10 x 10) to get 500 centimeters.
-
What is the process for adding mixed measurements?
To add mixed measurements, follow these steps: 1) Group like units together, 2) Add smaller units first, 3) Add larger units, 4) Combine the results, and 5) Rename and regroup if necessary. For example, when adding 2 liters, 900 milliliters + 1 liter, 100 milliliters, you would first add 900 mL + 100 mL = 1000 mL, then add 2 L + 1 L = 3 L, and finally combine to get 4 L (3 L + 1 L from 1000 mL).
-
How does subtraction with mixed measurements differ from addition?
Subtraction with mixed measurements often requires regrouping before performing the operation, especially when the top number in any unit is smaller than the bottom number. You may need to borrow from larger units and convert them to smaller units. For example, when subtracting 2 meters, 400 centimeters from 4 meters, 300 centimeters, you'd need to regroup 1 meter into 100 centimeters first.
-
What are some common challenges when working with metric units and how can they be overcome?
Common challenges include forgetting to align like units, making errors during unit conversion, and difficulty remembering the order of metric prefixes. To overcome these, always check that you're working with the same units before calculations, use a place value chart for conversions, and employ mnemonics like "King Henry Died By Drinking Chocolate Milk" to remember prefix order. Regular practice and creating real-life scenarios can also help master these concepts.
Prerequisite Topics for Operations with Metric Units
Understanding operations with metric units is crucial in various fields, from science and engineering to everyday life. To master this topic, it's essential to have a solid foundation in several prerequisite areas. One of the most fundamental skills is adding and subtracting decimals. This ability is directly applicable when working with metric measurements, as most metric units are based on the decimal system.
When performing operations with metric units, you'll often need to add or subtract measurements. For instance, calculating the total length of multiple objects or finding the difference between two distances requires proficiency in decimal arithmetic. Being comfortable with adding and subtracting decimals allows you to manipulate metric measurements accurately and efficiently.
Another crucial prerequisite topic is conversions involving squares and cubic units. This skill becomes particularly important when dealing with area and volume measurements in the metric system. Understanding how to convert between square meters and square centimeters, or cubic meters and cubic millimeters, is essential for solving complex problems involving metric units.
Visual aids can be incredibly helpful when learning about metric conversions. They provide a clear representation of the relationships between different units and can make the conversion process more intuitive. Mastering these conversions allows you to work seamlessly across different scales of measurement, which is often necessary in scientific and engineering applications.
Lastly, the ability to convert radicals to entire radicals may seem less directly related, but it's a valuable skill when working with metric units, especially in more advanced applications. This concept becomes relevant when dealing with square roots or cube roots of measurements, which can occur in various scientific and mathematical contexts involving metric units.
For example, when calculating the side length of a square given its area in square meters, you might encounter square roots. Similarly, finding the edge length of a cube given its volume in cubic meters would involve cube roots. Being able to manipulate these expressions efficiently can greatly simplify calculations involving metric units.
By mastering these prerequisite topics, you'll build a strong foundation for understanding and working with operations involving metric units. This knowledge will enable you to solve a wide range of problems, from simple everyday calculations to complex scientific and engineering challenges. Remember, each of these skills contributes to your overall proficiency in handling metric measurements, making your journey through more advanced mathematical and scientific concepts smoother and more intuitive.

