Describing patterns using tables and solving variables
Topic Notes
In this lesson, we will learn:
- How to describe number patterns using a function table (input output table)
- How to write formulas with variables for function tables and solve for variables
- The steps for solving the rule (one-step and two-step) or formula for a function table
Notes:
- We can think of the relationship between numbers in a pattern as a machine
- The machine takes the number you give it (the “input”), applies a function (the “rule” or math operations), and gives you a resulting number (the “output”)
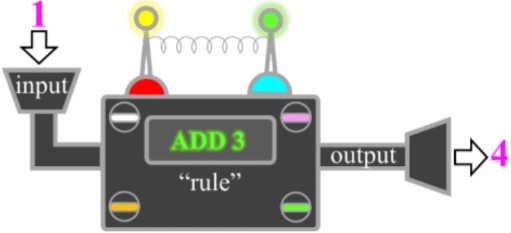
- The input output table (or function table) keeps track of these inputs and outputs
- Unlike the number sequence, order is not necessary for a function table
- Ex. for the number sequence/pattern “start at 1 and add 3 each time” it would be:

- Ex. but for the function table with a rule of “add 3” it could be:
- It is also possible to have two-step rules for function tables
- The first step is to either multiply or divide (× or ÷)
- The second step is to either add or subtract (+ or –)
- Instead of writing “input” and “output” in the function table, variables can be written instead
- Variables are symbols (letters) that represent values that can change (“varying”)
- Variables can be used to write a formula for the function table using the format:
- Or more commonly written as
- To solve for the variables in function tables:
- If solving for an output: plug the input value into the formula
- If solving for an input: plug the output value in and solve backwards (algebra)
- If you are given a complete function table and asked to solve for the formula:
- Check horizontally across input/output for one-step rules
- If it is not a one-step rule:
- If the inputs are consecutive, the multiplier m (in formula ) is the difference between outputs
- If the inputs are random, the formula can be either found by:
- (#1) trial and error
- OR (#2) using two pairs of input/output and m is the ratio of
Introduction to Patterns in Mathematics
Welcome to our exploration of patterns in mathematics! In this section, we'll dive into the fascinating world of mathematical patterns, focusing on how to describe them using tables and solve for variables. Our introduction video sets the stage for understanding these concepts, so be sure to watch it carefully. Patterns are everywhere in math, from simple number sequences to complex algebraic expressions. By learning to recognize and analyze patterns, you'll develop crucial problem-solving skills. Tables are powerful tools for organizing and visualizing patterns, making it easier to spot trends and relationships. We'll also explore how to use variables to represent unknown values in patterns, allowing us to solve more complex problems. Whether you're new to patterns or looking to deepen your understanding, this section will provide you with the foundation you need to succeed in mathematics. Let's embark on this exciting journey together!
Understanding Number Patterns and Sequences
Number sequences and patterns are fascinating aspects of mathematics that help us understand the order and logic behind numbers. These patterns are like puzzles waiting to be solved, and once you grasp the concept, you'll find them everywhere in the world around you!
So, what exactly are number sequences? They're simply a series of numbers that follow a specific rule or order. Think of them as a mathematical dance, where each number knows its next step based on a particular rhythm. For example, the sequence 2, 4, 6, 8, 10 follows the simple rule of adding 2 to each number to get the next one.
Identifying patterns in numbers is a crucial skill that helps develop logical thinking and problem-solving abilities. To spot a pattern, start by looking at how the numbers change from one to the next. Are they increasing? Decreasing? By how much? Is there a consistent operation happening between the numbers?
Let's look at some simple examples to help you understand better:
- 1, 3, 5, 7, 9 - This sequence increases by 2 each time.
- 2, 4, 8, 16, 32 - Each number is doubled to get the next one.
- 1, 1, 2, 3, 5, 8 - This is the famous Fibonacci sequence, where each number is the sum of the two before it.
To continue a pattern, you need to figure out the rule. Once you've identified how the numbers are changing, you can apply that rule to find the next numbers in the sequence. For instance, if we have the sequence 3, 6, 9, 12, and we know the rule is "add 3," we can easily continue it to 15, 18, 21, and so on.
Determining the rule of a sequence can be like being a detective. You need to observe carefully and look for clues. Here are some steps to help you crack the code:
- Look at the difference between consecutive numbers.
- Check if the numbers are being multiplied or divided by a constant value.
- See if there's a combination of operations happening.
- Consider if the pattern alternates or repeats after a certain number of terms.
For example, in the sequence 1, 4, 9, 16, 25, you might notice that these are all square numbers. The rule here is "square the position number" - so the 1st number is 1², the 2nd is 2², and so on.
Number patterns aren't just fun puzzles; they're incredibly useful in real life too! They help us predict trends, understand growth, and even create beautiful designs in art and architecture. By practicing with number sequences, you're training your brain to recognize patterns in all aspects of life.
Remember, the key to mastering number patterns is practice and curiosity. Don't be afraid to experiment and make mistakes - that's how we learn! Start with simple sequences and gradually move to more complex ones. Before you know it, you'll be spotting patterns everywhere and impressing everyone with your mathematical superpowers!
So, next time you encounter a series of numbers, take a moment to look for the hidden pattern. Who knows? You might just uncover a fascinating mathematical secret hiding in plain sight!
Introduction to Function Tables
Function tables are powerful tools in mathematics that help us understand and visualize the relationship between inputs and outputs in a systematic way. Unlike number sequences, which focus on a single series of numbers, function tables allow us to explore how one value (the input) affects another value (the output) based on a specific rule or pattern.
To understand function tables, let's start with a simple example. Imagine we have a rule that says "add 3 to the input." We can create a function table to show how this rule works:
| Input (x) | Output (y) |
|---|---|
| 1 | 4 |
| 2 | 5 |
| 3 | 6 |
In this table, we can see that for each input value, the output is always 3 more than the input. This is different from a number sequence, which might just list the outputs: 4, 5, 6. The function table gives us more information by showing both the inputs and outputs.
Here's how to fill out a function table step-by-step:
- Identify the rule or pattern that relates the input to the output.
- Create a table with two columns: one for input (often labeled x) and one for output (often labeled y).
- Choose a set of input values, usually starting with small, easy-to-work-with numbers.
- For each input value, apply the rule to find the corresponding output.
- Record both the input and output in the table.
Let's try another example. Suppose our rule is "multiply the input by 2 and then add 1." We can create a function table like this:
| Input (x) | Output (y) |
|---|---|
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
Function tables are excellent for spotting patterns in function tables. In this case, we can see that the output increases by 2 each time the input increases by 1. This pattern might not be as obvious if we only looked at the sequence of outputs (1, 3, 5, 7).
Function tables can also help us predict values for inputs we haven't calculated. If we understand the pattern, we can often figure out what the output would be for a larger input without having to do all the steps.
As students become more comfortable with function tables, they can tackle more complex rules and even use them to solve real-world problems with function tables. For instance, a function table could show how the cost of a taxi ride changes based on the distance traveled, or how the height of a plant changes over time.
To practice using function tables, try these steps:
- Start with a simple rule like "add 5 to the input" and create a function table.
- Try a slightly more complex rule, such as "double the input and subtract 1."
- Look for patterns in the outputs. Can you predict the next few outputs without calculating them?
- Create your own rule and challenge a friend to figure it out based on your function table.
Remember, function tables are all about exploring the relationship between inputs and outputs. They are excellent for spotting patterns in function tables and can be used to solve real-world problems with function tables.
Using Variables in Patterns
Let's dive into the exciting world of variables in mathematical patterns! Variables are like magic boxes that can hold different values, making them incredibly useful for describing understanding changing values in patterns and relationships. When we use variables, we can represent numbers that might change or values we don't know yet, which is super helpful in understanding changing values in patterns.
Imagine you're creating a function table to show how the cost of movie tickets changes based on the number of people in your group. Instead of writing out every possible number of people, we can use a variable like 'x' to represent the number of people. This variable can take on any value, allowing us to describe the pattern for any group size!
In patterns, we often talk about two types of variables: input variables and output variables. The input variable is like the question we're asking, while the output variable is the answer we get. For our movie ticket example, the number of people (x) would be the input variable, and the total cost (let's call it y) would be the output variable.
Here's a fun way to think about it: input variables are like the ingredients you put into a recipe, and output variables are like the delicious dish you get at the end. Just as changing the ingredients affects your final dish, changing the input variable affects the output variable in a pattern.
Using variables to describe patterns is like having a superpower in math! Instead of listing out every single possibility, we can write a simple expression or equation that works for any value. For example, if each movie ticket costs $10, we could describe the pattern as y = 10x. This tells us that no matter how many people are in the group (x), we can always find the total cost (y) by multiplying by 10.
Variables are incredibly versatile. They can represent all sorts of changing values in patterns. Maybe you're tracking how tall a plant grows each week, or how far a car travels at different speeds. By using variables, you can create models that work for any situation within the pattern.
Don't worry if it seems a bit tricky at first with practice, using variables in patterns becomes second nature. The more you play around with them, the more you'll see how they can simplify complex relationships and help you spot patterns more easily. Remember, variables are your friends in the math world, always ready to help you describe and understand changing values in patterns!
So next time you encounter a pattern, try identifying what's changing and give it a variable name. You might be surprised at how quickly you can uncover the underlying relationship and predict new values. With variables by your side, you're well-equipped to tackle any pattern that comes your way. Keep exploring, and have fun discovering the power of variables in mathematical patterns!
Writing Formulas for Patterns
Understanding how to write formulas to represent patterns in function tables is a crucial skill in mathematics. This ability allows students to analyze and predict relationships between variables efficiently. In this section, we'll explore the process of deriving formulas from function tables and understanding their components.
The General Formula Format: y = mx + b
The most common form of a linear function formula is y = mx + b, where:
- y represents the dependent variable (output)
- x represents the independent variable (input)
- m represents the slope (rate of change)
- b represents the y-intercept (starting point)
Steps to Determine the Formula from a Function Table
- Identify the pattern: Look for consistent changes between x and y values.
- Calculate the slope (m): Find the rate of change between y-values for each unit change in x.
- Determine the y-intercept (b): Use the slope and a point from the table to solve for b.
- Write the formula: Combine the slope and y-intercept in the y = mx + b format.
Example 1: Simple Linear Pattern
Consider this function table:
| x | y |
|---|---|
| 0 | 2 |
| 1 | 5 |
| 2 | 8 |
| 3 | 11 |
Step 1: The y-value increases by 3 for each increase in x.
Step 2: Calculating slope from table (m) = 3
Step 3: When x = 0, y = 2, so b = 2
Step 4: Formula: y = 3x + 2
Example 2: Negative Slope
Let's analyze this table:
| x | y |
|---|---|
| 0 | 10 |
| 1 | 7 |
| 2 | 4 |
| 3 | 1 |
Step 1: The y-value decreases by 3 for each increase in x.
Step 2: Calculating slope from table (m) = -3
Step 3: When x = 0, y = 10, so b = 10
Step 4: Formula: y = -3x + 10
Example 3: Fractional Slope
Consider this more complex table:
| x | y |
|---|---|
| 0 | 4 |
| 2 | 5 |
| 4 | 6 |
| 6 | 7 |
Step 1: The y-value increases by 1 for every 2 increases in x.
Step 2: Slope (m) = 1/2
Step 3: When x = 0, y = 4, so b = 4
Step 4: Formula: y = 1/2x + 4
Solving Problems with Pattern Tables
Pattern tables are powerful tools for problem-solving in mathematics, especially when dealing with sequences and functions. In this section, we'll explore various techniques to solve problems using pattern tables, including one-step rules, two-step rules, trial and error method, and the change in y over change in x method.
One-Step Rules
One-step rules involve a single operation to transform the input (x) into the output (y). Let's look at an example:
| x | y |
|---|---|
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
To find the rule, we observe that each y-value is 2 more than the corresponding x-value. Thus, the one-step rule is: y = x + 2
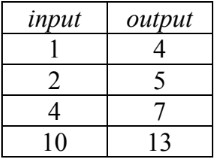
Two-Step Rules
Two-step rules involve two operations to transform x into y. Consider this example:
| x | y |
|---|---|
| 1 | 4 |
| 2 | 7 |
| 3 | 10 |
| 4 | 13 |
Here, we first multiply x by 3, then add 1. The two-step rule is: y = 3x + 1
Trial and Error Method
When the pattern isn't immediately obvious, we can use trial and error. Let's practice with this table:
| x | y |
|---|---|
| 2 | 6 |
| 3 | 11 |
| 4 | 18 |
| 5 | 27 |
Step 1: Try a one-step rule. We see it's not addition or multiplication alone.
Step 2: Try a two-step rule. Let's test y = x² + 2:
For x = 2: 2² + 2 = 6 (matches)
For x = 3: 3² + 2 = 11 (matches)
For x = 4: 4² + 2 = 18 (matches)
For x = 5: 5² + 2 = 27 (matches)
We've found our rule: y = x² + 2
Change in y over Change in x Method
This method is useful for linear relationships. Let's use this table:
| x | y |
|---|---|
| 1 | 4 |
| 2 | 7 |
| 3 | 10 |
| 4 | 13 |
Step 1: Calculate the change in y for each step: 3, 3, 3
Step 2: Calculate the change in x for each step: 1, 1, 1
Step 3: Divide change in y by change in x: 3/1 = 3
Step 4: This gives us a linear relationship.
Conclusion
In this lesson, we explored the essential skills of describing patterns using tables and solving variables. The introduction video laid a crucial foundation for understanding these concepts, emphasizing their importance in mathematical problem-solving. We learned how to identify and analyze patterns using tables, construct tables to represent data, and use variables to express relationships. These skills are fundamental in various mathematical applications and real-world scenarios. To reinforce your learning, it's vital to practice with diverse pattern problems, ranging from simple sequences to more complex algebraic expressions. Challenge yourself with different types of patterns and table representations to strengthen your analytical abilities. Remember, mastering these concepts opens doors to advanced mathematical thinking. We encourage you to continue exploring patterns and variables in your studies and daily life. For further engagement, try creating your own pattern problems or join online math forums to discuss and solve challenging examples with peers.
Introduction to Describing Patterns using Tables and Solving Variables: What is a function machine and what is a function table?
Step 1: Understanding Patterns and Number Sequences
In this lesson, we start by understanding the concept of patterns, specifically focusing on number sequences. Patterns are essentially things that repeat over and over again. By observing these patterns, we can predict what happens next. For number patterns, we look at the sequence of numbers, understand the rule that governs the sequence, and use this rule to predict the next number. For example, if we start at one and the rule is to add three each time, we can predict the next numbers in the sequence.
Step 2: Introduction to Functions
Next, we delve into the concept of functions. A function is a relationship between two numbers. This relationship can be represented using a function machine. A function machine is a conceptual tool that helps us understand how functions work. You provide an input number to the machine, it performs a mathematical operation (the function), and then it gives you an output number. This process helps us visualize the relationship between the input and output numbers.
Step 3: The Function Machine in Action
To understand how a function machine works, consider a simple rule: adding three to the input number. If you input the number one into the machine, it adds three and outputs the number four. If you input the number four, it adds three and outputs the number seven. This demonstrates the predictable nature of functions, as the same rule is applied consistently to any input number.
Step 4: Transition to Function Tables
After understanding the function machine, we move on to function tables. A function table, also known as an input-output table, is a way to represent the operations of a function machine in a tabular format. The table has two columns: one for the input numbers and one for the output numbers. This table helps us keep track of the inputs and their corresponding outputs, making it easier to see the pattern.
Step 5: Creating a Function Table
To create a function table, we take the inputs and outputs from the function machine and list them in the table. For example, if the input is one and the output is four, we write this pair in the table. If the input is four and the output is seven, we add this pair to the table as well. This process continues for any number of inputs and outputs, allowing us to see the pattern clearly.
Step 6: Advantages of Function Tables
Function tables offer several advantages over simple number sequences. One key advantage is that the inputs do not have to be in sequential order. You can input any number, and the function will still apply the same rule to give you the output. This flexibility allows for a broader range of inputs and makes it easier to see the overall pattern. For example, you can input the number 50, and the function will add three to give you 53. Similarly, you can input the number two, and the function will add three to give you five.
Step 7: Conclusion
In conclusion, understanding function machines and function tables is crucial for describing patterns using tables and solving variables. A function machine helps us visualize the relationship between input and output numbers, while a function table provides a clear and organized way to represent this relationship. By using these tools, we can better understand and predict number patterns, making it easier to solve problems involving variables.
FAQs
Here are some frequently asked questions about patterns, tables, and variables:
-
What is the difference between a number sequence and a function table?
A number sequence is a list of numbers that follow a specific pattern, while a function table shows the relationship between input (x) and output (y) values based on a rule. Function tables provide more information by displaying both inputs and outputs, whereas number sequences typically only show the output values.
-
How do I identify the rule in a pattern?
To identify the rule in a pattern, look for consistent changes between consecutive terms or between input and output values. Observe if numbers are being added, subtracted, multiplied, or divided. For more complex patterns, try to express the relationship using algebraic expressions or equations.
-
What is the purpose of using variables in patterns?
Variables in patterns allow us to represent unknown or changing values. They help us describe general relationships between inputs and outputs, making it possible to create formulas that work for any value within the pattern. This is especially useful for predicting future values or solving for specific inputs or outputs.
-
How can I write a formula for a pattern in a function table?
To write a formula for a pattern in a function table, first identify the relationship between x and y. Calculate the slope (rate of change) and y-intercept (starting point). Then, use the general form y = mx + b, where m is the slope and b is the y-intercept. Adjust this formula as needed for more complex patterns.
-
What methods can I use to solve problems with pattern tables?
Several methods can be used to solve problems with pattern tables: 1. One-step rules for simple patterns involving a single operation. 2. Two-step rules for patterns requiring two operations. 3. Trial and error method for more complex patterns. 4. Change in y over change in x method for linear relationships. Choose the method that best fits the complexity of the pattern you're analyzing.
Prerequisite Topics
Understanding patterns and describing them using tables while solving variables is a crucial skill in mathematics. To master this topic, it's essential to have a solid foundation in several prerequisite concepts. Let's explore how these fundamental topics contribute to your understanding of patterns and tables.
First and foremost, a strong grasp of number sequences is vital. Number sequences form the basis of many patterns, and recognizing these sequences helps in identifying and describing more complex patterns. By understanding how numbers progress in a sequence, you'll be better equipped to analyze and predict patterns in tables.
Another crucial prerequisite is understanding the relationship between two variables. This concept is fundamental when working with patterns in tables, as it allows you to see how changes in one variable affect another. Recognizing these relationships is key to describing patterns accurately and solving for unknown variables.
When dealing with patterns in tables, you'll often encounter linear relationships. Knowledge of graphing from slope-intercept form is invaluable here. This skill helps you visualize the pattern and understand how to calculate slope from a table, which is essential in describing linear patterns.
Understanding the domain and range of a function is also crucial. This knowledge helps you identify the possible input and output values in a pattern, which is particularly useful when working with tables and solving for variables. It provides context for the pattern and helps in determining reasonable solutions.
When it comes to solving variables in patterns, experience with distance and time related questions in linear equations can be incredibly helpful. These types of problems often involve patterns and tables, and the skills learned here directly apply to solving variables in various pattern-based scenarios.
Lastly, a solid foundation in understanding tables of values of linear relationships is essential. This skill directly relates to describing patterns using tables and helps in recognizing how values change within patterns. It's the cornerstone of working with tabular data and identifying underlying patterns.
By mastering these prerequisite topics, you'll be well-prepared to tackle more complex problems involving patterns, tables, and variable solving. Each of these concepts builds upon the others, creating a comprehensive understanding that will serve you well in your mathematical journey. Remember, a strong foundation in these basics is key to success in more advanced mathematical concepts.

