What is SohCahToa?
When you hear SohCahToa, it may sound like a different language entirely. But it's actually an easier way for you to remember how to use sine, cosine and tangent. These three are the main functions that you'll deal with in trigonometry problems.
SohCahToa stands for:
It can help you find the length of a side of a right triangle as long as you have an angle and some info on the other sides of the triangle.
Is SohCahToa only for right triangles
Yes, SohCahToa is only for right triangles. That's because only right triangles have a hypotenuse. Depending on which angle (whichever angle it is, it's called the angle ) you're using, you'd then figure out what the opposite or the adjacent is.
The adjacent side is always next to the angle. It's the side next to the angle that is not the hypotenuse. The opposite side is simply the side that's opposite of the angle.
Once you have several of the components given to you in a question, you'll be able to figure out unknowns that aren't given! You should also review how to find hypotenuse before we proceed. We'll try a question below to put Soh Cah Toa into use.
how to use SohCahToa
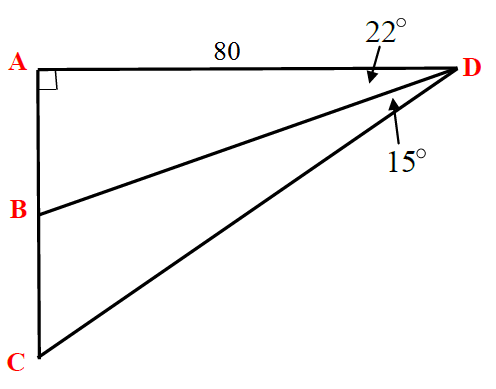
Question 1:
Find the length of
Solution:
ABD is a right angle triangle by itself. This means we can look for using tan. Tan takes the opposite over the hypotenuse (Toa in SohCahToa).
°
Now that we've got , we can look for using tan. ACD is also a right angle triangle, so we can use SohCahToa. Again, we're making use of Toa in SohCahToa.
°
We know the lengths of and , which means we can subtract the length of from in order to just get the length of .
= 28 cm
A lot of the questions you'll be given require you to put to use several of the trig ratios. You'll always be working with right triangles, so make sure to keep a note of that when you start the question. For example, this question seemed to require you to use BCD at first, but you know that can't be right because it is not a right triangle. Without that 90 degree right angle, you won't be able to use SohCahToa to help you find the unknowns.
Always base your answers around the right triangles in the question and you'll be able to find the answer.
Up for a challenge? Try out this online math test to see if you can answer these trigonometry questions quizzing you on Soh Cah Toa.
A lesson to review that deals with sine, cosine, and tangent includes the ASTC rule. You can also look into these lessons that covers how to find unknowns using the law of sines and the law of cosines. Studying how to find exact values of trigonometric ratios and trig ratios of angles in radians will also advance you further in trig problems