Arcs of a circle
Topic Notes
Introduction to Arcs of a Circle
Welcome to our exploration of arcs of a circle! This fundamental concept in circle terminology is crucial for understanding more advanced geometric principles. An arc is simply a portion of the circumference of a circle, and it's a key element in many mathematical calculations. In our introduction video, we'll dive deep into what arcs are, how they're measured, and their relationship to other parts of a circle. This video is an essential starting point for grasping the concept fully. As we progress, you'll see how arcs play a vital role in various real-world applications, from architecture to engineering. Remember, mastering arcs is like unlocking a new level in your geometry skills! Don't worry if it seems challenging at first with practice and patience, you'll soon become comfortable working with arcs. So, let's get started on this exciting journey through circle terminology, beginning with these fascinating curved segments!
Understanding Circle Terminology
Circles are fundamental geometric shapes that play a crucial role in mathematics and various real-world applications. To fully grasp the concepts related to circles, it's essential to understand the basic terminology associated with them. In this section, we'll explore key terms such as radius, diameter, circumference of a circle, central angle of a circle, and arcs, providing clear examples and explanations to illustrate these concepts.
Radius
The radius is a line segment that extends from the center of a circle to any point on its circumference. It is one of the most fundamental measurements of a circle and is typically denoted by the letter "r". The radius is crucial for calculating circle properties, including its area and circumference. For example, in a circle with a radius of 5 units, any straight line from the center to the edge would measure 5 units in length.
Diameter
The diameter is a line segment that passes through the center of the circle and has its endpoints on the circumference. It is the longest chord of the circle and is always twice the length of the radius. The diameter is usually represented by the letter "d". Using our previous example, if the radius is 5 units, the diameter would be 10 units. The relationship between radius and diameter can be expressed as d = 2r.
Circumference
The circumference of a circle is the distance around the circle, or the length of the circular boundary. It is analogous to the perimeter of other shapes. The circumference is directly related to both the radius and diameter of the circle. The formula for calculating the circumference is C = 2πr or C = πd, where π (pi) is approximately 3.14159. For a circle with a radius of 5 units, the circumference would be approximately 31.4 units.
Central Angle
A central angle of a circle is an angle formed by two radii of a circle, with its vertex at the center of the circle. Central angles are measured in degrees or radians and play a crucial role in understanding arcs and sectors of a circle. The measure of a central angle is directly proportional to the length of the arc it subtends on the circumference. For instance, a central angle of 90° (a quarter of a full rotation) would correspond to a quarter of the circle's circumference.
Arcs
An arc is a portion of the circumference of a circle. Arcs are typically defined by two points on the circle's circumference and the central angle that subtends them. There are two types of arcs:
Minor Arc
A minor arc is the smaller of the two possible arcs between two points on a circle's circumference. It is always less than or equal to 180°. For example, if we have a central angle of 60°, the minor arc would be the portion of the circumference that corresponds to this 60° angle.
Major Arc
A major arc is the larger of the two possible arcs between two points on a circle's circumference. It is always greater than 180° but less than 360°. Using the same example, if we have a central angle of 60°, the major arc would be the remaining portion of the circumference, corresponding to a 300° angle.
Relationships Between Circle Terms
Understanding the relationships between these terms is crucial for solving problems involving circles:
- The radius is half the diameter: r = d/2
- The diameter is twice the radius: d = 2r
- The circumference is π times the diameter: C = πd
- The circumference is 2π times the radius: C = 2πr
- The arc length formula is proportional to its central angle: Arc length = (θ/360°) × C, where θ is the central angle in degrees
These relationships allow us to calculate various properties of a circle when given limited information. For instance, if we
Types of Angles in a Circle
Circles are fundamental geometric shapes that contain various types of angles, each with unique properties and relationships. Two of the most important types of angles found in circles are central angles and inscribed angles. Understanding these angles and their relationship to arcs is crucial for mastering circle geometry.
A central angle is an angle formed by two radii of a circle that intersect at the center. The vertex of a central angle is always at the circle's center, and its sides are radii. Central angles play a significant role in measuring arcs and determining the portion of a circle's circumference they subtend. The measure of a central angle is equal to the measure of the arc it intercepts on the circle's circumference. For example, a 90-degree central angle intercepts a quarter of the circle's circumference, while a 180-degree central angle intercepts half of the circumference.
Inscribed angles, on the other hand, are angles formed by two chords of a circle that intersect on the circle's circumference. The vertex of an inscribed angle lies on the circle itself, unlike central angles. One of the most important properties of inscribed angles is that an inscribed angle is always half the measure of the central angle that subtends the same arc. This relationship is known as the Inscribed Angle Theorem and is fundamental to many geometric proofs and problem-solving techniques involving circles.
The relationship between central angles, inscribed angles, and arcs is crucial for understanding angle measurement in circles. An arc is a portion of a circle's circumference, and its measure is directly related to the central angle that subtends it. The measure of an arc is typically expressed in degrees and is equal to the measure of the central angle that intercepts it. For instance, if a central angle measures 60 degrees, the arc it intercepts will also measure 60 degrees.
When working with inscribed angles, it's important to remember that an inscribed angle is always half the measure of the central angle subtending the same arc. This means that if an inscribed angle intercepts an arc of 60 degrees, the inscribed angle itself will measure 30 degrees. This relationship holds true regardless of where the vertex of the inscribed angle is located on the circle's circumference, as long as it intercepts the same arc.
To illustrate these concepts, consider a circle with a central angle of 120 degrees. This central angle will intercept an arc measuring 120 degrees on the circle's circumference. If we draw an inscribed angle that intercepts the same arc, it will measure 60 degrees, which is half the measure of the central angle. This example demonstrates the direct relationship between central angles, inscribed angles, and the arcs they intercept.
Understanding these relationships is essential for solving various geometric problems involving circles. For instance, when given the measure of an inscribed angle, one can easily determine the measure of the arc it intercepts by doubling the angle's measure. Conversely, if the measure of an arc is known, the measure of any inscribed angle intercepting that arc can be found by halving the arc's measure.
In conclusion, central angles and inscribed angles are two fundamental types of angles found in circles, each with distinct properties and relationships to arcs. Central angles have their vertex at the circle's center and measure the same as the arc they intercept, while inscribed angles have their vertex on the circle's circumference and measure half the central angle subtending the same arc. These relationships form the basis for many geometric principles and problem-solving techniques involving circles, making them essential concepts in the study of circle geometry.
Chords and Tangents
In geometry, circles are fundamental shapes that possess unique properties, particularly when it comes to chords and tangents. Understanding these concepts is crucial for solving various geometric problems and appreciating the elegance of circular geometry.
A chord is a line segment that connects two points on a circle's circumference. It essentially "cuts" through the circle, creating two arcs on either side. The longest chord in a circle is its diameter, which passes through the center and divides the circle into two equal halves. Chords have several interesting properties:
- The perpendicular bisector of a chord always passes through the center of the circle.
- Equal chords in a circle are equidistant from the center.
- Chords of equal length subtend equal angles at the center.
On the other hand, a tangent is a line that touches the circle at exactly one point, called the point of tangency. This point of contact is unique, and the tangent line is perpendicular to the radius drawn to that point. Key properties of tangents include:
- A tangent line is perpendicular to the radius at the point of tangency.
- Two tangents drawn from an external point to a circle are always equal in length.
- The line joining the center of the circle to the external point bisects the angle between the two tangents.
The relationship between chords and tangents is fascinating. As a chord moves closer to the edge of the circle, it becomes shorter. In the limit, when the chord reaches the edge, it becomes a tangent, touching the circle at a single point. This transition illustrates the continuous nature of geometric relationships.
Arcs, which are portions of the circle's circumference, are intimately related to both chords and tangents. A chord defines two arcs on a circle, while a tangent can be thought of as defining an arc of zero length at the point of tangency. The measure of an arc is directly related to the central angle it subtends, which in turn is related to the length of the chord that connects its endpoints.
To illustrate these concepts, consider a circle with center O and radius r. Draw a chord AB and a tangent line touching the circle at point T. The perpendicular bisector of chord AB will pass through the center O. If we draw a radius OT to the point of tangency, it will be perpendicular to the tangent line. The angle formed between the tangent and a chord drawn from the point of tangency is equal to the angle in the alternate segment.
These relationships have numerous practical applications. In engineering, tangent lines are crucial for designing roads, as they represent the ideal path for a vehicle to follow when entering or exiting a curved section. In physics, the concept of tangents is fundamental to understanding motion along curved paths. Chords find applications in music theory, where they represent combinations of notes played simultaneously.
Understanding chords and tangents also provides a foundation for more advanced geometric concepts. For instance, the power of a point theorem relates the lengths of segments of intersecting chords or secants. The alternate segment theorem connects tangents and chords in a beautiful way, showing how angles in different parts of the circle are related.
In conclusion, chords and tangents are essential elements of circle geometry, each with unique properties and relationships to arcs. Their study not only enhances our understanding of geometric principles but also provides valuable tools for solving real-world problems in various fields. By mastering these concepts, we gain a deeper appreciation for the elegant symmetry and harmony inherent in circular shapes.
Calculating Arc Length
Understanding how to calculate the length of an arc in a circle is a fundamental skill in geometry. An arc is a portion of the circumference of a circle, and its length can be determined using various methods. In this comprehensive guide, we'll explore different approaches to finding the length of an arc, including proportional methods and formulas involving the central angle.
Method 1: Using Proportions
One straightforward way to calculate the length of an arc is by using proportions. This method relies on the relationship between the central angle, the full circle (360 degrees), and the circumference of the circle.
Step 1: Determine the central angle of the arc in degrees.
Step 2: Calculate the circumference of the entire circle using the formula C = 2πr, where r is the radius.
Step 3: Set up the proportion: (Central Angle / 360°) = (Arc Length / Circumference)
Step 4: Solve for the arc length.
Example:
Given: A circle with a radius of 5 units and a central angle of 45°
Step 1: Central angle = 45°
Step 2: Circumference = 2π(5) = 10π units
Step 3: 45° / 360° = Arc Length / 10π
Step 4: Arc Length = (45 / 360) * 10π 3.93 units
Method 2: Arc Length Formula
A more direct approach to finding the length of an arc is by using the arc length formula. This formula combines the radius of the circle and the measure of the central angle to calculate the arc length efficiently.
The arc length formula is: L = (θ / 360°) * 2πr
Where:
L = Length of the arc
θ = Measure of the central angle in degrees
r = Radius of the circle
Example using the same circle as before:
Given: Radius = 5 units, Central angle = 45°
L = (45° / 360°) * 2π(5)
L = 0.125 * 10π 3.93 units
Method 3: Using Radians
When working with radians instead of degrees, the arc length formula becomes even simpler. Radians are a natural unit for measuring angles in a circle, where 2π radians equal a full circle (360°).
The arc length formula using radians is: L = θr
Where:
L = Length of the arc
θ = Measure of the central angle in radians
r = Radius of the circle
To convert degrees to radians: θ (in radians) = θ (in degrees) * (π / 180°)
Example:
Given: Radius = 5 units, Central angle = 45°
Step 1: Convert 45° to radians: 45° * (π / 180°) = π/4 radians
Step 2: Apply the formula: L = (π/4) * 5 = 5π/4 3.93 units
Practical Applications
Understanding how to find the length of a circle's arc is crucial in various real-world scenarios. Architects might use this knowledge when designing arched doorways or windows. Engineers apply these calculations in the construction of circular structures like stadiums or amphitheaters. Even in everyday life, knowing how to calculate arc length can be useful for tasks such as measuring curved paths or determining the amount of material needed for a arc length in real-world scenarios.
Applications of Arcs in Real-World Scenarios
Arcs of a circle play a crucial role in various fields, including architecture, engineering, and design. Understanding these geometric shapes is essential for creating functional and aesthetically pleasing structures and objects. In architecture, arcs are widely used in the construction of bridges, domes, and archways. The famous St. Louis Gateway Arch, for instance, is a prime example of how arcs can be utilized to create iconic landmarks. This 630-foot tall structure is formed by a weighted catenary arch, which distributes the load evenly and provides stability to the monument.
In engineering, arcs are fundamental in the design of load-bearing structures. The arch bridge, one of the oldest types of bridges, relies on the principles of arcs to distribute weight and pressure effectively. The Pont du Gard in France, an ancient Roman aqueduct, showcases how arcs can be used to create sturdy and long-lasting structures. Modern suspension bridges also incorporate arcs in their design, with the main cables forming catenary curves to support the deck.
The automotive industry also benefits from the application of arcs. Car designers use arcs to create aerodynamic shapes that reduce drag and improve fuel efficiency. The curved windshields and body panels of vehicles are carefully designed using arc segments to optimize performance and aesthetics. In aerospace engineering, the wings of aircraft often incorporate arc shapes to generate lift and improve maneuverability.
In the field of design, arcs are essential elements in creating visually appealing products and graphics. Logo designers frequently use arcs to convey motion, unity, or completeness. The Nike swoosh, for example, is a simple yet powerful arc that has become one of the most recognizable logos worldwide. In product design, arcs are used to create ergonomic shapes that fit comfortably in the human hand, such as the curved handles of tools and utensils.
The construction of sports facilities also relies heavily on the principles of arcs. Stadium roofs often feature large-scale arches that provide both structural support and an impressive visual impact. The Wembley Stadium in London boasts a massive 133-meter-high arch that not only supports the roof but also serves as an iconic landmark. In conclusion, the real-world applications of arcs of a circle are vast and varied, demonstrating the importance of this geometric concept in shaping our built environment and everyday objects.
Common Mistakes and Misconceptions
When dealing with arcs of a circle, students often encounter several common mistakes and misconceptions. Understanding these errors and learning strategies to avoid them is crucial for mastering this important geometric concept. One frequent misconception is confusing arc length with chord length. Students may mistakenly measure the straight-line distance between the endpoints of an arc instead of calculating the curved distance along the circle's circumference. To avoid this, it's essential to visualize the arc as part of the circle's curved boundary rather than a straight line.
Another common error is misinterpreting central angles and their relationship to arcs. Students might assume that the measure of an arc is always equal to its central angle, forgetting that arc measure is typically expressed in degrees while arc length is a linear measurement. To reinforce correct understanding, practice converting between degrees and length units, emphasizing the difference between these two aspects of arcs.
Confusion often arises when dealing with major and minor arcs. Students may struggle to identify which arc is being referred to when given two points on a circle. A helpful strategy is to always specify whether you're discussing the major or minor arc, and to remember that a major arc is greater than 180 degrees while a minor arc is less than or equal to 180 degrees.
Many students also have difficulty with the concept of inscribed angles and their relationship to central angles and arcs. A common misconception is thinking that an inscribed angle has the same measure as the arc it intercepts. In reality, an inscribed angle is half the measure of the central angle that subtends the same arc. To reinforce this concept, practice drawing diagrams and comparing inscribed and central angles that intercept the same arc.
When calculating arc length, a frequent error is using the wrong formula or forgetting to convert degree measures to radians when necessary. To avoid this, always double-check which formula is appropriate for the given information and remember to use π radians = 180 degrees for conversions. Additionally, students often struggle with sector area calculations, confusing them with arc length formulas. A helpful tip is to remember that sector area involves squaring the radius, while arc length does not.
Lastly, a common problem-solving mistake is not sketching diagrams or labeling given information clearly. Encourage students to always draw and label diagrams, even for seemingly simple problems. This visual representation can help identify key relationships and prevent errors in calculations. By addressing these common mistakes and misconceptions, students can develop a stronger understanding of arcs of a circle and improve their problem-solving skills in geometry.
Conclusion
In this article, we've explored the fascinating world of arcs of a circle, a fundamental concept in circle geometry. We've covered key points such as the definition of arcs, their types, and how to calculate their length and area. The introduction video provided a visual and interactive way to grasp these concepts, making them more accessible to learners of all levels. Understanding arcs of a circle is crucial for various applications in mathematics, engineering, and real-world problem-solving. To truly master this topic, we encourage you to practice problems regularly, applying the formulas and techniques discussed. Don't hesitate to explore further resources on circle geometry to deepen your knowledge. Remember, mastering arcs of a circle opens doors to more advanced geometric concepts and enhances your overall mathematical skills. Keep exploring, practicing, and expanding your understanding of this essential aspect of circle geometry.
Find the length of the arc in red.
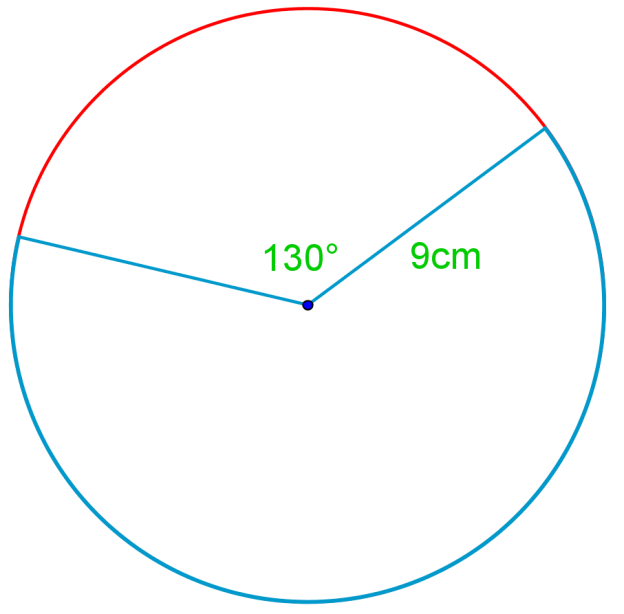
Step 1: Understand the Problem
The problem requires us to find the length of the arc highlighted in red. To solve this, we need to use the formula for arc length. The arc length formula is given by:
Arc Length (A) = θ × r
where θ is the angle in radians and r is the radius of the circle.
Step 2: Identify the Given Information
From the problem, we have the following information:
- The angle θ is given as 130 degrees.
- The radius r of the circle is 9 centimeters.
Step 3: Convert the Angle to Radians
The formula for arc length requires the angle to be in radians. Therefore, we need to convert the given angle from degrees to radians. The conversion formula is:
Radians = Degrees × (π / 180)
Applying this formula:
θ (in radians) = 130 × (π / 180)
Step 4: Calculate the Arc Length
Now that we have the angle in radians, we can use the arc length formula. Plug in the values of θ (in radians) and r into the formula:
Arc Length (A) = θ × r
Substitute θ with the converted radian value and r with 9 centimeters.
Step 5: Perform the Calculation
Use a calculator to perform the multiplication. Ensure that you use the value of π (pi) accurately to get the correct result. The calculation will give you the length of the arc in centimeters.
Step 6: Include the Units
After calculating the arc length, don't forget to include the units in your final answer. Since the radius was given in centimeters, the arc length will also be in centimeters.
Conclusion
By following these steps, you can accurately determine the length of the arc in red. Remember to always convert the angle to radians when using the arc length formula and to include the correct units in your final answer.
FAQs
Here are some frequently asked questions about arcs of a circle:
1. What is the formula for the arc length of a circle?
The formula for arc length is L = (θ / 360°) × 2πr, where L is the arc length, θ is the central angle in degrees, and r is the radius of the circle. For angles in radians, the formula simplifies to L = θr.
2. How do you find the length of the arc of a circle?
To find the length of an arc, you need to know the radius of the circle and the central angle that subtends the arc. Use the formula L = (θ / 360°) × 2πr, where θ is the central angle in degrees. If you have the angle in radians, use L = θr.
3. What is the formula for the area of an arc?
The area of a sector (region bounded by an arc and two radii) is given by A = (θ / 360°) × πr², where θ is the central angle in degrees and r is the radius. This isn't the area of the arc itself, but the area of the sector it defines.
4. What are the three types of arcs?
The three main types of arcs are: 1) Minor arc: less than half the circumference, 2) Major arc: more than half the circumference, and 3) Semicircle: exactly half the circumference. Each type is defined by the central angle it subtends.
5. How many arcs are there in a circle?
There are infinitely many arcs in a circle. Any two points on a circle's circumference define two arcs - a minor arc and a major arc. As you can choose any two points on the circumference, there are infinitely many possible arcs.
Prerequisite Topics
Understanding the arcs of a circle is a crucial concept in geometry, but to fully grasp this topic, it's essential to have a solid foundation in several prerequisite areas. These fundamental concepts not only provide the necessary background knowledge but also help in developing a deeper understanding of circular arcs and their properties.
One of the most important prerequisites is circles and circumference. Knowing how to calculate the circumference of a circle is vital because arcs are portions of the circle's circumference. This knowledge allows students to relate the length of an arc to the overall circumference, providing a crucial context for understanding arc measurements.
Another key concept to master is central and inscribed angles in circles. The central angle of a circle directly corresponds to the arc it subtends, making this relationship fundamental to working with arcs. Understanding how central angles relate to arc measures is essential for solving problems involving circular arcs.
Chord properties are also closely related to arcs. Chords are line segments that connect two points on a circle's circumference, and their properties often intersect with arc-related concepts. For instance, the perpendicular bisector of a chord always passes through the center of the circle and bisects the arc subtended by the chord.
Similarly, tangent properties play a role in understanding arcs. Tangents are lines that touch the circle at exactly one point, and their properties can be useful in solving problems that involve both tangents and arcs, especially in more advanced geometric constructions.
For those delving deeper into calculus applications, knowledge of the arc length of polar curves becomes relevant. While this may seem advanced, understanding the arc length formula in simpler contexts can provide valuable insights into how arcs behave and are measured in more complex scenarios.
Lastly, proficiency in converting between degrees and radians is crucial when working with arcs. Arcs can be measured in both degrees and radians, and the ability to convert between these units is essential for solving a wide range of problems involving circular arcs.
By mastering these prerequisite topics, students will find themselves well-equipped to tackle the complexities of arcs in circles. Each of these concepts contributes to a comprehensive understanding of circular geometry, allowing for a smoother transition into more advanced topics and applications involving arcs. Remember, a strong foundation in these areas will not only make learning about arcs easier but will also enhance overall problem-solving skills in geometry and related fields.

