Classifying polygons
Topic Notes
In this lesson, we will learn:
- How to name polygons: triangles, quadrilaterals, pentagons, hexagons, heptagons, and octagons
- How to classify regular vs. irregular polygons
- How to read markings on polygons: hashmarks for congruent sides, semicircles for congruent angles, arrows for parallel sides, and squares (right angles) for perpendicular sides
Notes:
- Polygons are 2D shapes with straight sides only. All polygons have sides (straight lines/edges) and vertices (corners/points where sides meet).
- Polygons are named by the number of sides they have:
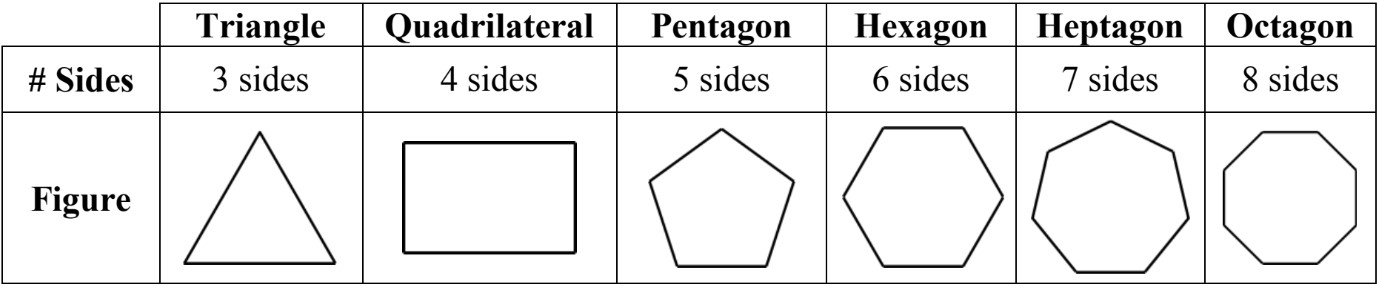
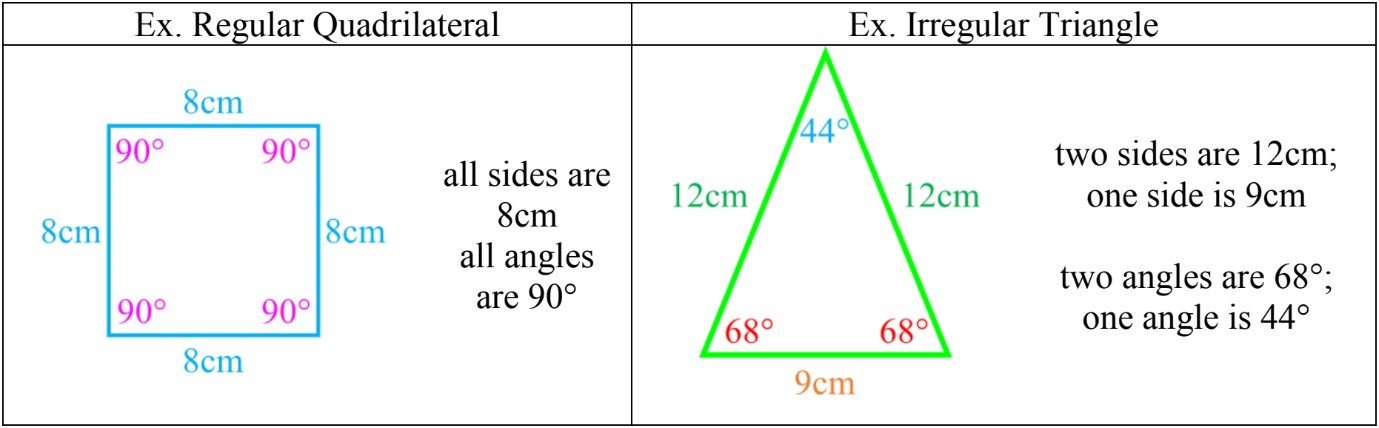
- Polygons can be regular or irregular. Regular polygons have congruent sides and angles; all sides and all angles are equal. Irregular polygons do not have same size sides and angles.
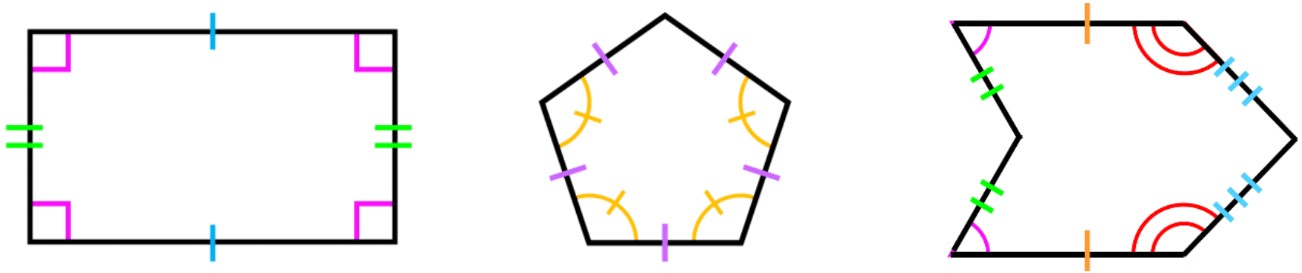
- Congruent sides can be shown with hashmarks (matching lines on the sides that are equal)
- Congruent angles can be shown with either semicircles with hashmarks, or with concentric circles
Introduction to Classifying Polygons
Welcome to our lesson on classifying polygons, an essential topic in geometry. We'll begin with an introductory video that provides a visual foundation for understanding these fascinating 2D shapes. This video is crucial as it demonstrates the key concepts we'll explore throughout the lesson. Polygons are closed, two-dimensional figures with straight sides, and learning to classify them is a fundamental skill in geometry. Our lesson will cover the precise definition of polygons, delving into their various attributes such as sides, angles, and vertices. We'll then explore how these characteristics are used to classify polygons into different categories. By the end of this lesson, you'll be able to identify and categorize various polygons based on their unique features. This knowledge forms the basis for more advanced geometric concepts and real-world applications in fields like architecture and design.
Understanding Polygons and Their Attributes
Polygons are fascinating two-dimensional shapes that play a crucial role in geometry and everyday life. By definition, polygons are 2D shapes composed exclusively of straight sides. This unique characteristic sets them apart from other shapes like circles or curved figures. The word "polygon" itself comes from the Greek language, where "poly" means "many" and "gon" means "angle" or "corner."
Two key attributes define polygons: sides and vertices. Sides are the straight lines that form the boundary of the polygon, while vertices are the points where these sides meet, commonly referred to as corners. To illustrate these concepts, let's consider the example from the video: a simple triangle. In this case, the triangle has three straight sides and three vertices where these sides intersect.
Counting the sides and vertices of a polygon is a fundamental skill in geometry. To count the sides, simply tally up the number of straight lines that make up the shape's perimeter. For vertices, count the number of points where these lines meet. In our triangle example, we can easily identify three sides and three vertices.
As we explore more complex polygons, such as squares, pentagons, or hexagons, this counting principle remains the same. A square has four sides and four vertices, a pentagon has five of each, and so on. This brings us to an important rule in polygon geometry: the number of sides in a polygon always equals the number of vertices.
This one-to-one correspondence between sides and vertices is a defining characteristic of polygons. It holds true regardless of the polygon's complexity or the number of sides it possesses. Whether you're dealing with a simple triangle or a complex 20-sided icosagon, you'll find that the number of straight lines forming the shape's boundary matches the number of corners where these lines meet.
Understanding this relationship is crucial for various applications, from basic geometry problems to more advanced mathematical concepts. It also helps in recognizing and classifying polygons in the world around us. Buildings, road signs, and many everyday objects often incorporate polygonal shapes in their design.
As you encounter polygons in your studies or daily life, remember to observe their straight sides and count both the sides and vertices. This practice will reinforce your understanding of these 2D shapes and their fundamental properties. Whether you're analyzing a simple geometric figure or a complex architectural design, the principles of sides and vertices in polygons remain constant.
In conclusion, polygons are 2D shapes defined by their straight sides and vertices. The number of sides always equals the number of vertices, creating a perfect balance in these geometric figures. This fundamental concept forms the basis for more advanced studies in geometry and helps us appreciate the structured beauty of polygonal shapes in our environment.
Types of Polygons Based on Number of Sides
Polygons are fascinating geometric shapes that surround us in both nature and human-made structures. The naming convention for polygons is based on the number of sides they possess, with each name having a unique etymology rooted in ancient Greek. Let's explore these shapes, starting with the simplest polygon and progressing to more complex ones.
The triangle, with its three sides, is the most fundamental polygon. The word "triangle" comes from the Latin "triangulus," meaning "three-cornered." Triangles are the only polygon that cannot be pushed inward or outward at a corner, making them inherently stable. This stability is why triangles are often used in construction, such as in roof trusses or bridge supports. In nature, triangles can be found in the shape of pine trees or in the facets of a cut diamond.
Moving to four sides, we encounter quadrilaterals. The term combines the Latin "quadri-" (four) with "latus" (side). Squares and rectangles are the most common quadrilaterals, but this category also includes rhombuses and trapezoids. Quadrilaterals are abundant in our daily lives, from the screens of our devices to the pages of books and the shape of most rooms.
Pentagons, with five sides, derive their name from the Greek "pente" (five) and "gonia" (angle). The most famous pentagon is likely the U.S. Department of Defense headquarters. In nature, many flowers have five petals arranged in a pentagonal shape, and starfish typically have five arms forming a pentagon.
Hexagons, six-sided polygons, come from the Greek "hex" (six). These shapes are incredibly efficient in terms of space usage, which is why bees construct their honeycombs in hexagonal patterns. Hexagons are also found in the molecular structure of graphene and in the shape of snowflakes.
Heptagons, with seven sides, are less common but no less interesting. The name combines "hepta" (seven) in Greek with "gonia." While not as prevalent in nature, heptagons can be found in some architectural designs and in certain crystals.
Octagons, eight-sided polygons, derive from the Greek "okto" (eight). The most recognizable octagon for many is the stop sign, chosen for its distinct shape that's easily identifiable from various angles. In architecture, octagonal towers and gazebos are popular for their aesthetic appeal and panoramic views.
It's worth noting that three sides is the minimum number required to form a polygon. This is because a polygon, by definition, is a closed shape made up of straight lines. With only two sides, it's impossible to enclose a space. The triangle, therefore, represents the simplest possible polygon, forming the foundation for all other polygonal shapes.
As we progress beyond octagons, the naming convention continues with Greek numerical prefixes: nonagon (9 sides), decagon (10 sides), hendecagon (11 sides), dodecagon (12 sides), and so on. While these higher-order polygons are less common in everyday life, they play important roles in mathematics, crystallography, and advanced architectural designs.
Understanding the naming convention of polygons not only helps in geometry but also enhances our appreciation of the world around us. From the triangular stability of bridges to the hexagonal efficiency of honeycombs, polygons demonstrate how mathematical principles underpin both natural phenomena and human innovation. By recognizing these shapes in our environment, we can gain a deeper understanding of the geometric patterns that shape our world and the language used to describe them.
Regular vs. Irregular Polygons
Polygons are closed, two-dimensional shapes with straight sides. They come in various forms, but can be broadly categorized into two main types: regular polygons and irregular polygons. Understanding the difference between these two categories is crucial in geometry and many real-world applications.
Regular polygons are characterized by two key features: all sides are of equal length, and all interior angles have the same measure. This uniformity gives regular polygons a symmetrical and balanced appearance. Some common examples of regular polygons include equilateral triangles, squares, and regular pentagons. In an equilateral triangle, all three sides are the same length, and all three angles measure 60 degrees. Similarly, a square has four equal sides and four right angles (90 degrees each).
On the other hand, irregular polygons do not have this consistency in their sides or angles. They may have sides of different lengths or angles of varying measures. Irregular polygons are more diverse in their appearance and can take on a wide range of shapes. For instance, a rectangle is an irregular polygon because, while its opposite sides are equal, all four sides are not necessarily the same length. Similarly, a trapezoid, with its two parallel sides of unequal length, is another example of an irregular polygon.
To illustrate the difference, consider a regular hexagon and an irregular hexagon. A regular hexagon has six equal sides and six equal angles, each measuring 120 degrees. It looks perfectly symmetrical from any angle. An irregular hexagon, however, might have sides of varying lengths and angles of different measures, resulting in an asymmetrical shape.
The concept of congruence is closely related to the discussion of regular and irregular polygons. In geometry, congruent figures have the same size and shape. In the context of polygons, congruence refers to the equality of corresponding sides and angles. In a regular polygon, all sides are congruent to each other, and all angles are congruent as well. This congruence is what gives regular polygons their distinctive symmetry and balance.
For irregular polygons, while they may not have overall congruence, they can still have congruent elements. For example, a rectangle has two pairs of congruent sides and four congruent right angles, even though it's classified as an irregular polygon due to its unequal side lengths.
Understanding the distinction between regular and irregular polygons is important in various fields. In architecture and design, regular polygons are often used for their aesthetic appeal and structural stability. Irregular polygons, with their versatility, are frequently encountered in nature and are useful in representing complex shapes in mapping and computer graphics.
In conclusion, regular polygons are defined by their equal sides and equal angles, exhibiting perfect symmetry and congruence among all their elements. Irregular polygons, while still closed shapes with straight sides, lack this uniform consistency in their sides and angles. Both types play significant roles in geometry and have numerous practical applications in the real world. Recognizing and understanding these differences enhances our ability to analyze and work with various shapes in both mathematical and practical contexts.
Marking Conventions in Polygons
Understanding the marking conventions used in polygon diagrams is essential for interpreting geometric shapes and their properties. These visual cues provide valuable information about the relationships between sides and angles within a polygon. Let's explore the key marking conventions and their significance in geometric representations.
One of the most common markings you'll encounter in polygon diagrams is the use of hash marks to indicate equal sides. These small, parallel lines are placed on the sides of a polygon to show that they have the same length. For example, in an equilateral triangle, you might see two sides marked with a single hash mark each, indicating that these sides are equal in length. In a square, all four sides would typically have the same number of hash marks, signifying that all sides are equal.
Similarly, arc marks are used to denote equal angles within a polygon. These curved lines are drawn inside the angles of the shape, with equal angles receiving the same number of arc marks. In an equilateral triangle, for instance, all three angles would be marked with a single arc, indicating that they are all 60 degrees. This convention helps quickly identify symmetry and regular shapes without the need for explicit angle measurements.
Parallel sides in polygons are another important feature that is often marked in diagrams. The convention for indicating parallel sides is to use arrows pointing in the same direction on the parallel sides. These arrows are typically drawn as small, single-headed arrows near the middle of the sides they represent. In a parallelogram, you would see two pairs of sides marked with these parallel arrows, clearly showing the defining characteristic of this quadrilateral.
Perpendicular sides, which meet at right angles, have their own special marking convention. The standard symbol for a right angle is a small square drawn in the corner where the perpendicular sides meet. This square represents the familiar "L" shape of a right angle and is instantly recognizable in geometric diagrams. In a rectangle, you would see this right angle symbol in all four corners, indicating that all its angles are 90 degrees.
These marking conventions are not just arbitrary symbols; they play a crucial role in conveying important information about the properties of polygons at a glance. By using hash marks, arc marks, parallel arrows, and right angle symbols, geometers can communicate complex relationships without relying solely on written descriptions or numerical measurements. This visual language of geometry allows for quick and intuitive understanding of shapes and their characteristics.
In practice, you might encounter these markings in various combinations. For example, a rhombus would typically show equal side lengths with hash marks on all sides, while also indicating two pairs of parallel sides with arrows. An isosceles right triangle would combine hash marks on two sides to show their equality, along with a right angle symbol in one corner.
It's important to note that the absence of these markings doesn't necessarily mean the properties they represent are not present. Sometimes, diagrams may be simplified or certain properties may be stated in accompanying text. However, when present, these markings provide valuable visual cues that can greatly aid in problem-solving and geometric reasoning.
As you become more familiar with these conventions, you'll find that you can quickly assess the properties of a polygon just by glancing at its diagram. This skill is invaluable in geometry, as it allows for rapid identification of shape types and properties, which is often the first step in solving more complex geometric problems.
Remember, these marking conventions are standardized across most geometric texts and resources, making them a universal language for communicating about shapes and their properties. By mastering the interpretation of hash marks, arc marks, parallel side indicators, and right angle symbols, you'll be well-equipped to tackle a wide range of geometric challenges and to communicate your own geometric ideas effectively.
Practical Applications of Polygon Classification
Polygon classification plays a crucial role in various real-world applications, spanning architecture, design, and nature. Understanding and identifying different types of polygons enhances problem-solving skills and spatial reasoning abilities, making it an essential concept in many fields. In architecture, polygons form the foundation of building design and structural integrity. Architects use triangles, rectangles, and more complex polygons to create aesthetically pleasing and structurally sound buildings. For instance, the hexagonal shape of honeycomb-inspired structures provides both strength and efficiency in modern architectural designs. In urban planning, city layouts often incorporate polygonal shapes to optimize space utilization and traffic flow. Design professionals rely heavily on polygon classification in their work. Graphic designers use polygons to create logos, illustrations, and user interfaces. The simplicity of triangles and squares often conveys stability and trustworthiness in branding, while more complex polygons can add visual interest and uniqueness. In product design, understanding polygons helps in creating ergonomic and functional objects, from furniture to electronic devices. Nature itself is a master of polygon utilization. From the hexagonal cells of a beehive to the pentagonal structure of many flowers, polygons are abundant in the natural world. The study of these natural polygons has inspired biomimicry in engineering and design, leading to more efficient and sustainable solutions. For example, the tessellating hexagons found in a turtle's shell have inspired lightweight yet strong materials for protective gear. Problem-solving and spatial reasoning skills are significantly enhanced through the study of polygons. In mathematics and geometry, polygon classification forms the basis for more advanced concepts like tessellations and transformations. These skills translate directly into real-world problem-solving, such as optimizing packaging designs or creating efficient storage solutions. Understanding polygons also aids in map reading and navigation, essential skills in fields like geography and urban planning. Students are encouraged to observe and identify polygons in their everyday environment. From the octagonal shape of a stop sign to the rectangular tiles on a floor, polygons are everywhere. This awareness not only reinforces learning but also helps in developing a keen eye for patterns and shapes. In technology, polygon classification is fundamental in computer graphics and 3D modeling. Video game designers use polygons to create realistic environments and characters, while CAD (Computer-Aided Design) software relies on polygonal structures for precision in engineering and manufacturing. The applications of polygon classification extend even to fields like agriculture, where precision farming techniques use polygonal field mapping for efficient crop management. By understanding the ubiquity and importance of polygons in the world around us, students can develop a deeper appreciation for geometry and its practical applications in various aspects of life and career paths.
Conclusion
In this lesson on classifying polygons, we've covered essential concepts that form the foundation of geometry. The introduction video provided a crucial visual understanding of these shapes, helping to solidify your grasp on the subject. Remember, polygons are classified based on their number of sides and angles, with key categories including triangles, quadrilaterals, pentagons, and beyond. We explored regular and irregular polygons, emphasizing the importance of equal sides and angles in regular shapes. To reinforce your learning, practice identifying and classifying polygons in your everyday surroundings from street signs to architectural elements. This real-world application will deepen your understanding and sharpen your skills. For continued learning, explore online geometry tools, solve polygon-related puzzles, or create your own polygon art project. By actively engaging with these concepts, you'll develop a strong foundation in polygon classification that will serve you well in future mathematical endeavors.
FAQs
-
What is the difference between regular and irregular polygons?
Regular polygons have all sides of equal length and all interior angles of equal measure. For example, a square is a regular polygon. Irregular polygons, on the other hand, have sides of different lengths or angles of different measures. A rectangle with unequal sides is an example of an irregular polygon.
-
How do you determine the number of sides in a polygon?
To determine the number of sides in a polygon, simply count the straight line segments that make up its perimeter. Each unbroken line segment counts as one side. For instance, a triangle has 3 sides, a square has 4 sides, and a pentagon has 5 sides.
-
What are the marking conventions used in polygon diagrams?
Common marking conventions include hash marks to indicate equal sides, arc marks to denote equal angles, arrows to show parallel sides, and small squares to represent right angles. These visual cues help quickly identify properties of polygons without needing explicit measurements.
-
Can a polygon have fewer than three sides?
No, a polygon must have at least three sides. By definition, a polygon is a closed, two-dimensional figure with straight sides. It's impossible to enclose a space with fewer than three straight lines, which is why a triangle is the simplest polygon.
-
What are some real-world applications of polygon classification?
Polygon classification has numerous practical applications. In architecture, polygons are used for building design and structural integrity. In graphic design, they're used to create logos and user interfaces. In nature, polygons are found in structures like honeycombs and snowflakes. Understanding polygons is also crucial in fields like computer graphics, urban planning, and even precision agriculture.
Prerequisite Topics
Understanding the foundations of geometry is crucial when delving into the topic of classifying polygons. While there are no specific prerequisite topics listed for this subject, it's important to recognize that a solid grasp of basic geometric concepts forms the bedrock for comprehending polygon classification.
Classifying polygons is a fundamental skill in geometry that builds upon several key concepts. For instance, familiarity with basic shapes and their properties is essential. Understanding what defines a polygon - a closed, two-dimensional figure made up of straight lines - is the starting point for classification.
Moreover, knowledge of angles plays a significant role in polygon classification. The number and types of angles within a polygon contribute to its classification. For example, recognizing right angles is crucial for identifying rectangles and squares within the broader category of quadrilaterals.
Another important aspect is the concept of symmetry. Many polygons exhibit various forms of symmetry, which can be a defining characteristic in their classification. Understanding rotational and reflective symmetry can help students identify regular polygons and appreciate the geometric beauty of shapes like equilateral triangles and regular hexagons.
The ability to measure and compare side lengths is also vital. This skill enables students to distinguish between different types of triangles (equilateral, isosceles, scalene) and recognize special quadrilaterals like rhombuses and parallelograms.
Furthermore, a basic understanding of geometric proofs and logical reasoning can enhance a student's ability to justify polygon classifications. While not always explicitly required, this skill can deepen comprehension and foster critical thinking in geometry.
Although there are no specific prerequisite topics listed, it's clear that a strong foundation in basic geometry is invaluable. Students who are comfortable with concepts such as lines, angles, and basic shapes will find themselves well-prepared to tackle the classification of polygons.
As students progress in their study of classifying polygons, they'll discover how this knowledge applies to more advanced geometric concepts and real-world applications. From architecture to computer graphics, the ability to recognize and classify polygons is a skill that extends far beyond the mathematics classroom.
In conclusion, while there may not be a formal list of prerequisites, the journey to mastering polygon classification is built upon a solid understanding of fundamental geometric principles. Students are encouraged to review these basic concepts if they feel unsure, as a strong foundation will greatly facilitate their learning and appreciation of polygon classification.

