Classifying triangles
Topic Notes
In this lesson, we will learn:
- How to classify triangles by their side lengths
- How to classify triangles by their angles
Notes:
- A triangle is a 2-dimensional (2D) shape with 3 straight sides and 3 angles
- A triangle’s angles always add up to 180° degrees
- Triangles can be classified in 2 ways:
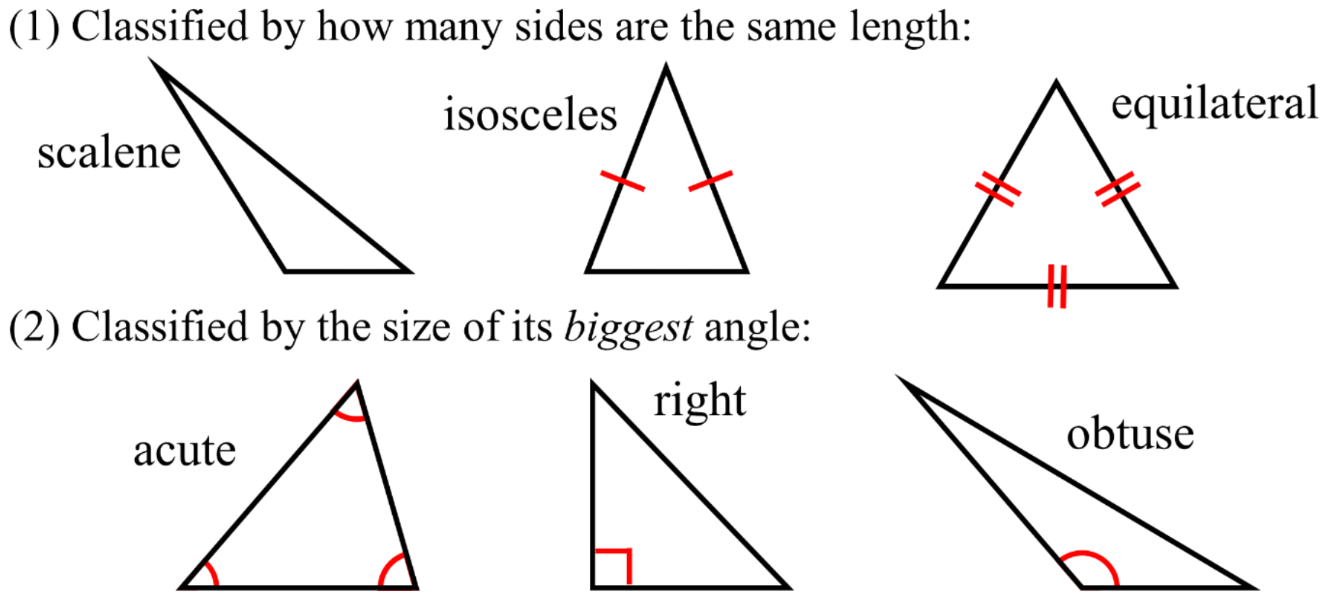
- By their side lengths
- By the size of their angles
- When looking at side lengths, we classify triangles by how many sides are the same length (how many sides are “congruent”)
- If no sides are the same, it is a scalene triangle
- If two sides are the same, it is an isosceles triangle
- If all three sides are the same, it is an equilateral triangle
- When looking at the angles, we classify triangles by its biggest angle and comparing it with the right angle (are the angles smaller than, equal to, or greater than 90° degrees?)
- If all of the angles are smaller than 90° , it is an acute triangle
- If one of the angles is exactly 90° , it is a right triangle
- If one of the angles is bigger than 90° , it is an obtuse triangle
Introduction to Classifying Triangles
Triangle classification is a fundamental concept in geometry that helps us understand and categorize different types of triangles. Our introduction video serves as an essential starting point for grasping this topic, providing a visual and engaging overview of triangle classification. As you'll learn, triangles can be classified based on two primary characteristics: their side lengths and angles. These classifications allow us to identify and describe triangles more precisely, which is crucial for various mathematical applications and real-world problem-solving. By understanding how to classify triangles according to their side lengths, you'll be able to distinguish between equilateral, isosceles triangles, and scalene triangles. Similarly, classifying triangles by their angles will introduce you to acute, right triangles, and obtuse triangles. This knowledge forms the foundation for more advanced geometric concepts and helps develop critical thinking skills in mathematics.
Understanding the properties of isosceles triangles is essential for solving various geometric problems. These triangles have two sides of equal length, which leads to two equal angles opposite those sides. This symmetry can simplify many calculations and proofs in geometry. On the other hand, right triangles are crucial in trigonometry, as they form the basis for defining trigonometric ratios such as sine, cosine, and tangent. Mastering the classification and properties of these triangles will significantly enhance your mathematical toolkit.
Understanding Triangle Basics
A triangle is a fundamental geometric shape that plays a crucial role in mathematics and various real-world applications. As a 2D shape, a triangle is defined by its three straight sides and three angles. This simple yet versatile figure is one of the most basic and important shapes in geometry. The unique properties of triangles make them essential in fields such as architecture, engineering, and design.
One of the key characteristics of a triangle is that it always has exactly three sides and three angles. These sides are straight lines that intersect at three points, called vertices. The shape is closed, meaning that the sides form a continuous boundary. This property distinguishes triangles from other geometric figures and contributes to their stability and strength in structural designs.
A fascinating and consistent feature of all triangles is that the sum of their interior angles sum is always 180 degrees. This property holds true regardless of the triangle's size or shape, whether it's an equilateral, isosceles, or scalene triangle. This constant interior angles sum is a fundamental principle in geometry and trigonometry, often used in calculations and proofs.
Triangles belong to a larger category of shapes known as polygons. A polygon is a closed 2D shape with straight sides. In this classification, triangles are the simplest polygons, having the fewest possible sides for a closed shape. Other polygons include quadrilaterals (four sides), pentagons (five sides), and so on. The triangle's position as the most basic polygon makes it a building block for understanding more complex geometric shapes and concepts.
The study of triangles extends beyond basic geometry. Their properties are essential in trigonometry, where the relationships between a triangle's sides and angles are explored in depth. These relationships form the basis for solving complex problems in physics, engineering, and navigation. Additionally, triangles are often used in art and design for their aesthetic appeal and structural integrity.
Understanding the basic properties of triangles is crucial for anyone studying geometry or related fields. The concept of a triangle as a 2D shape with three straight sides and three angles, along with the constant 180-degree sum of its angles, provides a foundation for more advanced mathematical concepts. As part of the polygon family, triangles serve as an introduction to more complex shapes, making them an essential starting point in the study of geometry and spatial relationships.
Classifying Triangles by Side Lengths
Triangles are fascinating geometric shapes that can be classified in various ways. One of the most fundamental methods of categorizing triangles is based on the lengths of their sides. This classification system gives us three distinct types of triangles: scalene, isosceles, and equilateral. Understanding these types is crucial for anyone studying geometry or working with triangular shapes in real-world applications.
Let's start with the scalene triangle. The term "scalene" comes from the Greek word "skalenos," meaning uneven or unequal. A scalene triangle is characterized by having all three sides of different lengths. In other words, no two sides of a scalene triangle are congruent. This type of triangle is the most common in nature and everyday objects. Visually, a scalene triangle appears asymmetrical, with no two angles being the same. When drawing or identifying a scalene triangle, each side is typically marked with a different symbol or length to emphasize their uniqueness.
Next, we have the isosceles triangle. The word "isosceles" is derived from the Greek "isoskeles," where "isos" means equal and "skelos" means leg. An isosceles triangle has two sides of equal length, also known as congruent sides. The third side, called the base, is of a different length. This type of triangle is symmetrical along the line that bisects the angle formed by the two equal sides. In geometric diagrams, isosceles triangles are often depicted with two sides marked with the same symbol to indicate their congruence. The base is usually marked differently to show its unique length.
The third type is the equilateral triangle, which is perhaps the most recognizable. "Equilateral" comes from the Latin words "aequus," meaning equal, and "latus," meaning side. As the name suggests, an equilateral triangle has all three sides of equal length. This perfect symmetry results in all three angles also being equal, each measuring exactly 60 degrees. Equilateral triangles are often used in architecture and design due to their aesthetic appeal and structural stability. When representing an equilateral triangle in diagrams, all three sides are typically marked with the same symbol to indicate their equal lengths.
Understanding how to identify these triangles using side markings is essential in geometry. In mathematical diagrams and textbooks, congruent sides are usually indicated by the same number of hash marks or by using the same letter to denote their length. For example, in an isosceles triangle, you might see two sides marked with a single hash mark each, while the third side has no mark or a different symbol. In an equilateral triangle, all three sides would have the same marking, such as a single hash mark on each side or the same letter (e.g., 'a') denoting their length.
The classification of triangles based on side lengths has practical applications beyond geometry class. In construction and engineering, understanding these triangle types is crucial for designing stable structures. Equilateral triangles, for instance, are often used in truss designs due to their inherent strength and load distribution properties. Isosceles triangles frequently appear in roof designs, while scalene triangles can be found in various architectural elements where asymmetry is desired.
It's worth noting that these classifications are not mutually exclusive with other triangle categorizations. For example, a right triangle (defined by having one 90-degree angle) can also be isosceles if two of its sides are equal. Similarly, an obtuse triangle (with one angle greater than 90 degrees) could be scalene if all its sides are of different lengths.
In conclusion, the three types of triangles based on side lengths - scalene, isosceles, and equilateral - form a fundamental part of geometric understanding. By recognizing the Greek and Latin origins of these terms, students can better remember their characteristics. The ability to identify these triangles through side markings is a valuable skill in geometry and related fields. Whether you're a student, an architect, or simply someone fascinated by shapes, understanding these triangle classifications provides a solid foundation for exploring more complex geometric concepts and their real-world applications.
Classifying Triangles by Angles
When it comes to understanding triangles, one of the most fundamental aspects is classifying them based on their angles. There are three main types of triangles defined by their angles: acute triangles, right triangles, and obtuse triangles. Each of these types has unique characteristics that set them apart, and understanding these differences is crucial in geometry and various real-world applications.
Let's start with the acute triangle. An acute triangle is a triangle where all three of its angles are less than 90 degrees. This means that each angle in an acute triangle is "sharp" or pointed. To visualize an acute triangle, imagine a slice of pizza with a very narrow point. The key feature to remember is that all angles in an acute triangle are less than a right angle.
Speaking of right angles, let's move on to the right triangle. A right triangle is defined by having one angle that measures exactly 90 degrees. This 90-degree angle is called the right angle, and it forms the cornerstone of trigonometry and many architectural designs. The right angle is often represented by a small square in the corner of the triangle. A helpful memory aid for right triangles is to think of the corner of a room where two walls meet the floor that's a right angle!
The third type is the obtuse triangle. An obtuse triangle has one angle that measures more than 90 degrees. This larger angle gives the triangle a somewhat "stretched out" appearance compared to acute or right triangles. To remember what an obtuse triangle looks like, think of the word "obtuse" as meaning "wider" or "more open" than a right angle.
The right angle, measuring 90 degrees, serves as a crucial reference point in distinguishing these three types of triangles. It's the dividing line between acute and obtuse angles. Any angle less than 90 degrees is acute, while any angle greater than 90 degrees is obtuse. This 90-degree benchmark is essential in various fields, from construction to engineering.
To accurately measure the angles in a triangle and determine its type, you'll need a tool called a protractor. A protractor is a semicircular or circular measuring instrument marked with degrees, typically from 0 to 180 or 0 to 360. Here's how to use a protractor to measure angles in a triangle:
- Place the center point of the protractor on the vertex of the angle you want to measure.
- Align the 0-degree mark with one side of the angle.
- Read where the other side of the angle intersects the protractor's scale.
- The number at this intersection point is the measure of the angle in degrees.
By measuring all three angles of a triangle with a protractor, you can easily determine whether it's acute, right, or obtuse. Remember, the sum of all angles in any triangle is always 180 degrees!
To help you visualize and remember these triangle types, consider these memory aids:
- Acute Triangle: Think "A" for Acute and "All angles less than 90°"
- Right Triangle: Visualize the "R" in Right as the right angle itself
- Obtuse Triangle: Remember "O" for Obtuse and "One angle Over 90°"
Understanding these three types of triangles acute, right, and obtuse is fundamental in geometry and has practical applications in various fields. Whether you're studying mathematics, working in construction, or simply appreciating the shapes around you, being able to identify and classify triangles based on their angles is a valuable skill. With practice and the use of tools like protractors, you'll soon find yourself easily recognizing these triangle types in both academic settings and the world around you.
Combining Side Length and Angle Classifications
Triangles can be classified using two distinct methods: by their side lengths and by their angles. When we combine these classification systems, we create a more comprehensive description of a triangle's properties, known as dual classification. This approach provides a deeper understanding of triangular shapes and their unique characteristics.
Let's first review the individual classification methods. By side length, triangles are categorized as equilateral (all sides equal), isosceles (two sides equal), or scalene (no sides equal). By angles, they are classified as acute (all angles less than 90°), right (one 90° angle), or obtuse (one angle greater than 90°). When we merge these systems, we can describe triangles with greater precision.
For example, an isosceles acute triangle combines properties from both classification methods. It has two equal sides and all angles less than 90°. This dual classification provides a clear picture of the triangle's shape and proportions. Similarly, a scalene right triangle has no equal sides and one angle greater than 90°, offering a distinct visual representation.
An equilateral acute triangle is a special case where all sides are equal, and all angles measure exactly 60°. This dual classification emphasizes the triangle's perfect symmetry and unique angular properties. It's important to note that all equilateral triangles are also acute triangles, demonstrating how some classifications naturally overlap.
When applying dual classification, it's crucial to understand that a triangle can only have one classification from each method. For instance, a triangle cannot be both isosceles and scalene, or both acute and obtuse. This principle ensures clarity and consistency in geometric descriptions.
Other examples of dual classifications include scalene right triangles (no equal sides, one 90° angle) and isosceles obtuse triangles (two equal sides, one angle greater than 90°). Each combination provides unique insights into the triangle's structure and properties.
By mastering dual classification, students and professionals can communicate more effectively about triangular shapes, enhancing their understanding of geometry and its applications in various fields such as architecture, engineering, and design. This comprehensive approach to triangle classification serves as a foundation for more advanced geometric concepts and problem-solving techniques.
Practical Applications of Triangle Classification
Triangle classification plays a crucial role in various real-world applications, particularly in architecture, engineering, and design. Understanding the different types of triangles and their properties is essential for problem-solving and construction in these fields. In architecture, triangles are fundamental to structural integrity and aesthetic design. The equilateral triangle, for instance, is often used in roof trusses due to its balanced distribution of forces. This application ensures stability and longevity in building structures. Right-angled triangles are indispensable in calculating dimensions and angles in construction plans, utilizing the Pythagorean theorem for precise measurements.
In engineering, triangle classification is vital for designing and analyzing structures. Bridge construction heavily relies on triangular shapes for their inherent strength and ability to distribute loads effectively. The Warren truss, a series of equilateral triangles, is commonly used in bridge design for its efficiency in load-bearing. Isosceles triangles find applications in the design of aircraft wings, where their symmetry contributes to aerodynamic performance. In mechanical engineering, cam mechanisms often employ triangular shapes for precise motion control in machinery.
The field of design also benefits significantly from triangle classification. Graphic designers use triangles to create dynamic and visually appealing compositions. The golden triangle, based on the golden ratio, is frequently employed in logo design and layout planning to achieve aesthetically pleasing proportions. In product design, understanding triangle types helps in creating ergonomic and functional objects. For example, the design of handheld tools often incorporates triangular grips for better comfort and control.
Problem-solving in various disciplines often involves triangle classification. In surveying and cartography, triangulation techniques use the properties of triangles to determine distances and positions accurately. This method is crucial in GPS technology and mapping. In computer graphics and 3D modeling, triangles are the basic building blocks for creating complex shapes and surfaces. The ability to classify and manipulate these triangles is essential for realistic rendering and efficient computation in video games and animation.
Understanding triangle types also plays a role in optimizing space and materials. In packaging design, triangular shapes can be used to create sturdy and space-efficient containers. In solar panel installation, the angle and orientation of panels, often determined using triangular calculations, are crucial for maximizing energy capture. These practical applications demonstrate how triangle classification, far from being a purely academic exercise, is a fundamental tool in shaping our built environment and solving complex real-world problems across multiple disciplines.
Conclusion
In summary, triangle classification is a fundamental concept in geometry that categorizes triangles based on their side lengths and angle measurements. The introduction video provides a comprehensive overview of the different types of triangles, including equilateral, isosceles, scalene, right, acute, and obtuse triangles. Understanding these classifications is crucial for solving geometric problems and analyzing shapes in various real-world applications. To reinforce your knowledge, it's essential to practice identifying triangle types using different examples and diagrams. This will help solidify your understanding and improve your ability to recognize triangles quickly. As you continue your geometry journey, explore additional resources such as interactive geometry tools, textbooks, and online tutorials to deepen your understanding of isosceles triangles and other geometric concepts. Remember, mastering triangle classification is a stepping stone to more advanced topics in geometry, making it a valuable skill for students and professionals alike.
FAQs
-
What are the three main types of triangles based on side lengths?
The three main types of triangles based on side lengths are:
- Equilateral: All three sides are equal in length.
- Isosceles: Two sides are equal in length.
- Scalene: No sides are equal in length.
-
How are triangles classified based on their angles?
Triangles are classified into three types based on their angles:
- Acute: All angles are less than 90 degrees.
- Right: One angle is exactly 90 degrees.
- Obtuse: One angle is greater than 90 degrees.
-
What is a right triangle and why is it important?
A right triangle is a triangle with one 90-degree angle. It's important because:
- It forms the basis for trigonometry.
- It's used in the Pythagorean theorem.
- It has numerous applications in construction and engineering.
-
Can a triangle be both isosceles and right-angled?
Yes, a triangle can be both isosceles and right-angled. This occurs when:
- Two sides are equal in length.
- One angle is 90 degrees.
- The other two angles are each 45 degrees.
-
What is the sum of angles in any triangle?
The sum of angles in any triangle is always 180 degrees. This is true for all triangles, regardless of their classification by sides or angles.
Prerequisite Topics for Classifying Triangles
Understanding the classification of triangles is a fundamental skill in geometry, but to truly master this concept, it's crucial to have a solid grasp of several prerequisite topics. These foundational elements not only enhance your understanding but also provide the necessary tools to analyze and categorize triangles effectively.
One of the most important prerequisites is the study of polygons. Triangles are the simplest polygons, and understanding the general properties of polygons, such as the sum of interior angles, lays the groundwork for triangle classification. This knowledge helps in recognizing how triangles fit into the broader context of geometric shapes.
Delving deeper into specific triangle types, familiarity with isosceles and equilateral triangles is essential. Understanding the properties of equilateral triangles, for instance, is crucial when classifying triangles based on their side lengths and angle measures. This knowledge forms the basis for identifying special cases within triangle classifications.
For more advanced classifications, particularly those involving right triangles, a strong foundation in trigonometry is invaluable. Knowing how to use cosine ratios to calculate angles and sides can be extremely helpful. These trigonometric ratios provide powerful tools for analyzing triangle properties, especially when dealing with non-right triangles or when indirect measurements are needed.
Similarly, the ability to use sine ratios to calculate angles and sides complements the cosine knowledge. Understanding how to use a protractor to measure angles accurately is a practical skill that directly applies to triangle classification, especially when dealing with physical measurements or constructions.
No discussion of triangle classification would be complete without mentioning the Pythagorean theorem. This fundamental principle is crucial for identifying right triangles and understanding the relationships between side lengths in various triangle types. Its applications extend far beyond simple classification, making it an indispensable tool in geometry.
By mastering these prerequisite topics, students gain a comprehensive toolkit for classifying triangles. Each concept builds upon the others, creating a robust understanding of triangle properties and relationships. This interconnected knowledge not only aids in classification but also enhances problem-solving skills and geometric reasoning abilities. As students progress in their geometry studies, they'll find that this strong foundation in triangle classification serves as a springboard for more advanced geometric concepts and applications.

