Introduction to volume of rectangular prisms

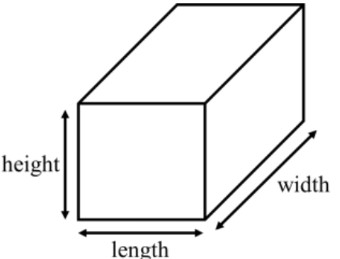
Introduction to Volume of Rectangular Prisms

Welcome to our lesson on the volume of rectangular prisms, a fundamental concept in 3D geometry. We'll begin with an engaging introduction video that sets the stage for our exploration of this important topic. This video will highlight the significance of understanding volume in real-world applications and everyday life. Building on your previous knowledge of cubic measure, we'll delve deeper into how volume applies specifically to rectangular prisms formula. These 3D shapes are all around us, from cereal boxes to shipping containers, making this lesson both practical and relevant. We'll learn how to calculate the volume of rectangular prisms formula using a simple formula, and understand why this measurement is crucial in fields like architecture, engineering, and packaging design. By the end of this lesson, you'll have a solid grasp of volume calculation for these common 3D shapes, setting a strong foundation for more advanced geometric concepts.

Understanding Dimensions and Geometric Properties

In geometry, dimensions play a crucial role in defining and understanding various shapes and objects. The three primary dimensions - length, width, and height - form the foundation of geometric properties and measurements. These dimensions are fundamental in describing the size and shape of objects in space, from simple lines to complex three-dimensional structures.

Length is the first dimension, representing the distance between two points in a straight line. Width, the second dimension, measures the breadth or side-to-side extent of an object. Height, the third dimension, describes the vertical distance from the base to the top of an object. Together, these three dimensions allow us to fully describe the spatial characteristics of any geometric shape.

The relationship between these dimensions and geometric properties becomes evident when we consider different types of measurements: one-dimensional (1D), two-dimensional (2D), and three-dimensional (3D). Each type of measurement corresponds to a specific geometric property and utilizes different combinations of the three dimensions.

One-dimensional measurements, such as perimeter, focus solely on length. The perimeter is the distance around the outer edge of a shape. For example, in a rectangular prism, the perimeter of any face would be calculated by adding up the lengths of all sides of that face. This measurement only considers the length dimension, making it a 1D property.

Two-dimensional measurements introduce the concept of area, which combines length and width. Area represents the amount of space covered by a flat surface. In the case of a rectangular prism, the area of any face would be calculated by multiplying its length by its width. This 2D property provides information about the size of surfaces but does not account for depth or height.

Three-dimensional measurements bring in the concept of volume, which incorporates all three dimensions: length, width, and height. Volume represents the amount of space occupied by a 3D object. For a rectangular prism, the volume is calculated by multiplying its length, width, and height. This 3D property gives us a complete understanding of the object's size in space.

To illustrate these concepts, let's consider a rectangular prism with dimensions of 5 units in length, 3 units in width, and 2 units in height. The perimeter of the front face would be 2(5 + 3) = 16 units, a 1D measurement. The area of the same face would be 5 × 3 = 15 square units, a 2D measurement. The volume of the entire prism would be 5 × 3 × 2 = 30 cubic units, a 3D measurement.

The concept of a unit cube is particularly useful in understanding these properties. A unit cube has dimensions of 1 × 1 × 1, making its volume exactly one cubic unit. We can think of our rectangular prism as being composed of 30 such unit cubes stacked together. This visualization helps in grasping how volume relates to the three dimensions and how it differs from area and perimeter.

Understanding these dimensional properties is essential in various fields, from architecture and engineering to physics and computer graphics. Architects use these concepts to design buildings, considering not just the floor area but also the volume of spaces. Engineers apply these principles in calculating material requirements and structural integrity. In computer graphics, 3D modeling relies heavily on manipulating objects in three-dimensional space, utilizing all aspects of length, width, and height.

In conclusion, the three dimensions of length, width, and height are fundamental in defining geometric properties. They allow us to progress from simple 1D measurements like perimeter to more complex 2D and 3D properties such as area and volume. By understanding how these dimensions interact and contribute to different geometric properties, we gain a deeper appreciation of the spatial world around us and the mathematical principles that govern it.

Calculating Volume of Rectangular Prisms

Understanding how to calculate the volume of rectangular prisms is an essential skill in mathematics and various real-world applications. The volume of rectangular prisms formula is a simple yet powerful tool that allows us to determine the amount of space occupied by three-dimensional objects. In this guide, we'll explore the volume formula, break down its components, and walk through the process of using it effectively.

The Volume Formula: V = l × w × h

The volume formula for a rectangular prism is expressed as V = l × w × h, where:

• V represents the volume
• l stands for length
• w represents width
• h denotes height

Step-by-Step Instructions for Using the Volume Formula

1. Identify the dimensions: Before applying the formula, it's crucial to correctly identify the length, width, and height of the rectangular prism. Remember that a rectangular prism has six faces, with opposite faces being identical rectangles.
2. Measure the length: The length is typically the longest dimension of the prism. Use a ruler, measuring tape, or any appropriate measuring tool to determine the length accurately.
3. Measure the width: The width is usually the second-longest dimension, perpendicular to the length. Measure it carefully, ensuring you're not confusing it with the height.
4. Measure the height: The height is the dimension perpendicular to both the length and width. It's often the vertical dimension when the prism is resting on its largest face.
5. Apply the formula: Once you have all three measurements, simply multiply them together using the formula V = l × w × h.
6. Include units: Remember to express your final answer in cubic units. If you measured in centimeters, your result would be in cubic units (cm³). If you used inches, the volume would be in cubic inches (in³).

Example Calculation

Let's walk through an example to illustrate how to use the volume formula:

Problem: Calculate the volume of a rectangular box with a length of 10 cm, a width of 5 cm, and a height of 3 cm.

Step 1: Identify the dimensions
Length (l) = 10 cm
Width (w) = 5 cm
Height (h) = 3 cm

Step 2: Apply the volume formula
V = l × w × h
V = 10 cm × 5 cm × 3 cm

Step 3: Perform the calculation
V = 150 cm³

Explanation: By multiplying the length (10 cm) by the width (5 cm) and then by the height (3 cm), we determine that the box has a volume of 150 cubic centimeters. This means it can hold 150 cubic centimeters of material or liquid.

Practical Applications

Understanding and applying the volume formula is crucial in various fields and everyday situations:

• Architecture and construction for calculating building material quantities
• Shipping and logistics for determining package sizes and cargo space
• Manufacturing for designing product packaging
• Home improvement for estimating paint or flooring needs
• Science experiments involving liquid or gas measurements

By mastering the volume formula and the process

Visualizing Volume with Unit Cubes

Visualizing volume using unit cubes is an effective way to understand the concept of three-dimensional space and measurement. Unit cubes are small, uniform blocks that represent one cubic unit of volume. By arranging these cubes in a 3D space, we can create tangible representations of volume that are easy to comprehend and calculate.

To begin visualizing volume with unit cubes, imagine a rectangular prism volume filled with these small cubes. Each cube touches its neighbors on all sides, creating a solid structure. This arrangement allows us to see how space is occupied in three dimensions: length, width, and height.

Counting unit cubes to determine volume is a straightforward process. Simply tally the total number of cubes used to fill the entire space. This method provides a concrete way to understand volume before introducing abstract formulas. For instance, if you have a structure that is 3 cubes long, 2 cubes wide, and 4 cubes tall, you would count a total of 24 unit cubes (3 × 2 × 4 = 24).

This counting method directly relates to the volume formula for rectangular prism volume: V = l × w × h (Volume equals length times width times height). By counting the cubes along each dimension and multiplying these numbers, we arrive at the same result as counting each cube individually. This connection helps students bridge the gap between concrete manipulation and abstract mathematical concepts.

In the video example, a rectangular prism is constructed using unit cubes. The base of the prism is 4 cubes long and 3 cubes wide, creating a foundation of 12 cubes (4 × 3 = 12). This base is then built up to a height of 2 cubes. By applying the volume formula, we can quickly calculate that the total volume is 24 cubic units (4 × 3 × 2 = 24). This result can be verified by physically counting all the unit cubes used in the structure.

Visualizing volume with unit cubes offers several benefits. It provides a tactile and visual representation of abstract concepts, making it easier for learners to grasp the idea of volume. This method also helps in understanding the relationship between area and volume, as students can see how the area of the base relates to the overall volume when height is added. Additionally, it lays a strong foundation for more complex volume calculations involving irregular shapes and curved surfaces.

By mastering the visualization of volume using unit cubes, students develop a solid understanding of 3D space and measurement. This skill is invaluable in various fields, including architecture, engineering, and design, where spatial reasoning and volume calculations are essential. The ability to mentally manipulate and understand 3D structures is a crucial skill that extends far beyond basic mathematics, making the unit cube method a powerful tool in spatial education.

Solving for Missing Dimensions

Algebra is a powerful tool for solving real-world problems, especially when it comes to finding missing dimensions in geometric shapes. One common application is using algebra to solve for an unknown dimension when given the volume of rectangular prism and two other dimensions of a three-dimensional object. This process involves manipulating the volume formula and applying algebraic principles to isolate the unknown variable. Let's explore how to use algebra to solve for a missing dimension, complete with a step-by-step example and guidance on handling units in calculations.

To begin, it's essential to understand the basic volume formula for the shape you're working with. For this example, we'll use a rectangular prism, where the volume (V) is calculated by multiplying length (l), width (w), and height (h): V = l × w × h.

Step 1: Identify the known and unknown variables
Let's say we know the volume of a rectangular prism is 120 cubic inches, its length is 6 inches, and its width is 5 inches. Our goal is to find the height.

Step 2: Write the equation using the known values
V = l × w × h
120 in³ = 6 in × 5 in × h

Step 3: Simplify the known dimensions
120 in³ = 30 in² × h

Step 4: Isolate the unknown variable (h) using algebra
To solve for h, we need to divide both sides of the equation by 30 in²:
120 in³ ÷ 30 in² = h
4 in = h

Step 5: Check the units
It's crucial to ensure that the units make sense throughout the calculation. In this case, we started with cubic inches (in³) and divided by square inches (in²), resulting in inches (in) for the height, which is correct.

This algebraic approach can be applied to various shapes and scenarios. For instance, if you're working with a cylinder and know its volume and radius but need to find its height, you would use the formula V = πr²h and solve for h using similar steps.

When solving for missing dimensions, it's important to pay attention to units and unit conversions. Sometimes, you may need to convert between different unit systems or scales. For example, if the volume is given in cubic feet but the length and width are in inches, you'll need to convert all measurements to the same unit before solving the equation.

Here's a quick guide for handling units in these calculations:

1. Ensure all measurements are in the same unit system (e.g., metric or imperial).
2. Convert all linear measurements (length, width, height) to the same unit (e.g., all in inches or all in centimeters).
3. Make sure the volume unit is the cube of the linear unit (e.g., cubic inches if working in inches).
4. Perform the calculation, keeping track of units throughout.
5. If necessary, convert the final answer to the desired unit.

Practicing these algebraic techniques for solving missing dimensions will enhance your problem-solving skills and spatial reasoning. It's a valuable skill in fields such as engineering, architecture, and design, where understanding and manipulating three-dimensional spaces is crucial.

Remember, the key to successfully solving for missing dimensions using algebra lies in clearly identifying the known and unknown variables, correctly applying the volume formula for the given shape, and carefully manipulating the equation to isolate the unknown dimension. By following these steps and paying close attention to units, you can confidently tackle a wide range of geometric problems and find missing dimensions with ease.

Real-World Applications of Volume

Understanding the volume of rectangular prisms has numerous practical applications in everyday life and various professional fields. This knowledge is essential for determining the capacity of containers, rooms, and objects, making it a valuable skill in both personal and professional contexts. Let's explore some real-world applications of volume calculations for rectangular prisms.

In the realm of home organization and storage, calculating volume helps in efficient space utilization. For instance, when purchasing storage containers for a closet or garage, knowing the volume allows you to select appropriately sized boxes that maximize available space. Similarly, when moving to a new home, understanding volume helps in estimating the number of moving boxes needed and determining if furniture will fit in specific rooms.

The food and beverage industry heavily relies on volume calculations. Manufacturers use this knowledge to design packaging for products like cereal boxes, milk cartons, and juice containers. Restaurants and bakeries apply volume calculations to determine portion sizes, recipe scaling, and ingredient storage. Even at home, understanding volume aids in meal planning and food storage, ensuring efficient use of refrigerator and pantry space.

In construction and architecture, volume calculations are crucial for various aspects of building design and material estimation. Architects use volume to determine room sizes, ensuring comfortable living spaces. Contractors calculate the volume of concrete needed for foundations or the amount of insulation required for walls. HVAC specialists use volume calculations to design efficient heating and cooling systems for buildings.

The shipping and logistics industry heavily relies on volume calculations. Courier services use these calculations to determine shipping costs based on package dimensions. Warehouses optimize their storage capacity by efficiently arranging boxes and containers based on their volumes. Even in personal scenarios, understanding volume helps in packing suitcases efficiently for travel.

In the field of environmental science, volume calculations are essential for water management. Engineers use this knowledge to design water tanks, reservoirs, and drainage systems. Conservationists apply volume calculations to estimate water usage in households and industries, promoting sustainable practices.

The automotive industry utilizes volume calculations in various ways. Car manufacturers design trunk spaces and fuel tanks based on volume considerations. Mechanics use volume calculations when dealing with engine components, such as determining oil capacity or coolant volume.

Understanding volume is also crucial in the medical field. Pharmacists use volume calculations for precise medication dosing. Medical equipment designers apply this knowledge when creating devices like IV bags or syringes. Even in everyday health practices, volume calculations help in maintaining proper hydration by tracking water intake.

These examples demonstrate the wide-ranging applications of volume of rectangular prisms in our daily lives and various professional fields. From organizing our homes to designing buildings, managing resources, and ensuring our health, the ability to calculate and understand volume plays a vital role in numerous aspects of our world.

Conclusion

In this lesson, we've explored the fundamental concept of volume and its practical applications. We learned the essential volume formula for rectangular prisms: V = l × w × h. This formula serves as the foundation for calculating the volume of more complex shapes. The introduction video played a crucial role in visualizing the concept and understanding its real-world relevance. Remember, volume is not just a mathematical concept but a practical tool used in various fields. To solidify your understanding, it's important to practice calculating volumes of different objects around you. Challenge yourself by exploring more complex shapes and their volume formulas. As you progress, you'll discover how this knowledge applies to fields like engineering, architecture, and manufacturing. Keep experimenting and don't hesitate to ask questions. Your journey into the world of volume has just begun, and there's so much more to discover!