Tangent Planes
Recall that in Calc I, linear approximation is about finding a linear equation tangent to a curve at a point, and using it to estimate values of the curve "near" that point. The equation of the tangent line at point would be:
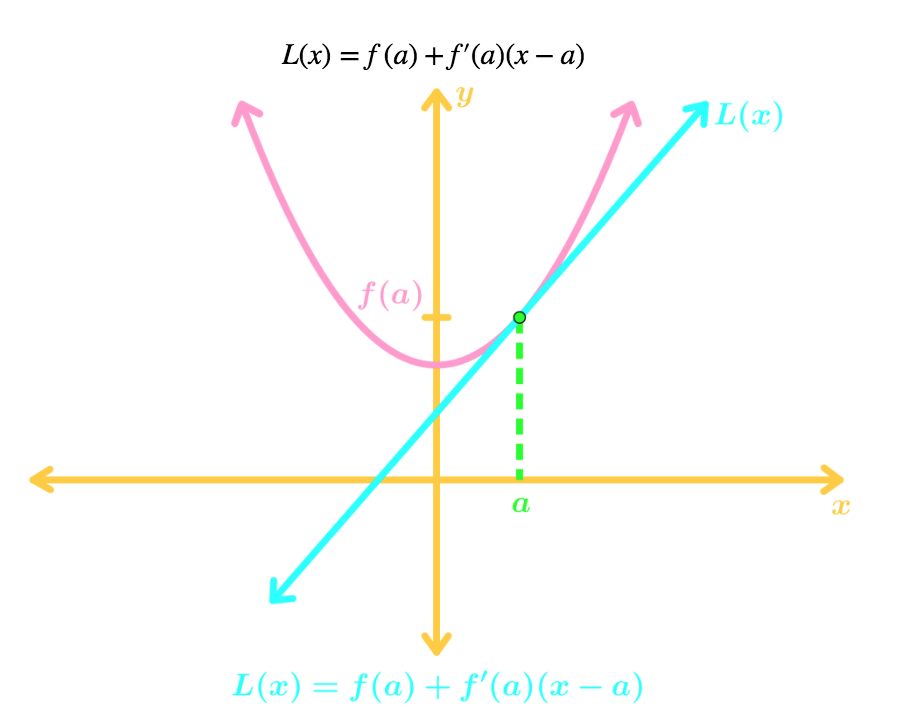
Calc III is similar, but now it is in 3D. Instead of 2D curves, we have 3D surfaces. Instead of tangent lines, we have tangent planes. The formula for the tangent plane at point is:
Linear Approximation
Just like how we can estimate values of a 2D curve, can also estimate the value of a 3D surface near a point using linear approximation. We say that if we are at the point , and we want to approximate a point near it (say ), then