Area and perimeter of parallelograms
Topic Notes
In this lesson, we will learn:
- The basic properties of the shape of the parallelogram
- How to understand and calculate the perimeter of a parallelogram
- How to understand and calculate the area of a parallelogram
Notes:
- A parallelogram is a 2D shape with 4 straight sides
- Each pair of sides (across from each other) are parallel and the same length
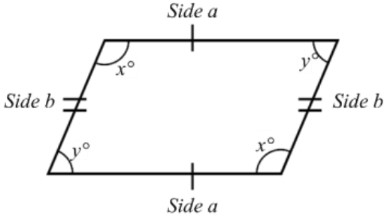
- The internal angles are not right angles (90°); otherwise it would be a rectangle
- Opposite angles are the same size
- A special parallelogram with all sides of equal length is called a rhombus
- The perimeter is the exact distance around the shape.
- Perimeter is a 1D (one-dimensional) quantity
- It uses units such as meters (m, cm, mm, km), miles (mi), yards (yd), or inches and feet (in and ft)
- For parallelograms, the formula is written as:
- Pparallelogram =
- Where is the length of one of the sides, and is the length of the other side
- The area is the space that is covered by the shape.
- Area is a 2D (two-dimensional) quantity
- It uses squared units such as square meters (m2, cm2, mm2, km2), square miles (mi2), square yards (yd2), or square inches and feet (in2 and ft2)
- For parallelograms, the formula is written as:
- Aparallelogram =
- Where is base, and is height
- A parallelogram’s height is not the same as the slant (side) length.

Introduction to Area and Perimeter of Parallelograms
Welcome to our lesson on parallelograms, a fundamental shape in geometry. We'll begin with an introductory video that sets the stage for our exploration of these fascinating quadrilaterals. This video is crucial as it provides a visual foundation for understanding parallelograms. Our lesson will delve into two key aspects of parallelograms: area and perimeter of parallelograms. These concepts are essential in geometry, forming the basis for more complex mathematical principles. By mastering the calculation of a parallelogram's area and perimeter of parallelograms, you'll gain insights into spatial relationships and learn to quantify enclosed spaces. Similarly, understanding perimeter will enhance your ability to measure boundaries and distances. These skills are not only vital for academic success but also have practical applications in fields like architecture and engineering. As we progress, you'll discover how the unique properties of parallelograms influence their area and perimeter calculations, setting them apart from other quadrilaterals.
Understanding Parallelograms
A parallelogram is a fascinating 2D shape that belongs to the family of quadrilaterals, meaning it has four sides. What sets a parallelogram apart from other four-sided shapes is its unique set of properties that make it both simple and intriguing. At its core, a parallelogram is defined by its parallel sides, which give it its distinctive appearance and mathematical characteristics.
The most fundamental feature of a parallelogram is that it has two pairs of parallel sides. This means that the opposite sides of the shape are always equal in length and run parallel to each other. Imagine drawing two parallel lines and then connecting their ends with two more lines you've just created a parallelogram! This property of parallel sides is what gives the parallelogram its name and is the key to understanding its other characteristics.
Another important property of parallelograms is that their opposite angles are congruent, or equal. This means that the angles at opposite corners of the shape have the same measure. This characteristic is directly related to the parallel nature of the sides. As the parallel sides extend, they create equal angles where they intersect with the other pair of sides.
When comparing parallelograms to rectangles, it's helpful to think of a parallelogram as a more generalized form of a rectangle. In fact, all rectangles are parallelograms, but not all parallelograms are rectangles. The key difference lies in the angles. While a rectangle always has four right angles (90 degrees each), a parallelogram can have angles of any measure, as long as the opposite angles are equal.
This brings us to the concept of a slanted rectangle, which is an excellent way to visualize a parallelogram. Imagine taking a rectangle and pushing one of its top corners to the side. The shape you end up with is a parallelogram. It retains the parallel sides of the original rectangle, but now the angles are no longer right angles. This slanted appearance is what gives many parallelograms their distinctive look.
Visually, a parallelogram can be described as a shape that looks like a leaning or tilted rectangle. The top and bottom sides remain parallel to each other, as do the left and right sides, but the overall shape appears skewed or slanted. This slant can vary greatly, from a slight tilt to a more dramatic lean, but the parallel nature of the opposite sides always remains constant.
The versatility of parallelograms makes them incredibly useful in various fields, from mathematics and geometry to art and design. Their unique properties allow for interesting calculations and applications in areas like physics and engineering. For instance, the area of a parallelogram can be calculated using the same formula as a rectangle (base × height), but the height must be measured perpendicular to the base, not along the slanted side.
In conclusion, parallelograms are defined by their parallel sides and equal opposite angles. They can be thought of as a more general form of rectangles, with the key difference being their potential for non-right angles. The concept of a slanted rectangle helps in visualizing this 2D shape, emphasizing its distinctive tilted appearance while maintaining the crucial parallel relationship between opposite sides. Understanding parallelograms opens up a world of geometric possibilities and provides a foundation for exploring more complex shapes and mathematical concepts.
Perimeter of Parallelograms
Understanding the perimeter formula for parallelograms is essential in geometry and real-world applications. The perimeter formula for a parallelogram is a straightforward concept that relates to the one-dimensional property of shapes. In this section, we'll explore the perimeter formula, its components, and how to apply it effectively.
The perimeter of a parallelogram is defined as the total straight line distance around its outer edges. To calculate this, we use the perimeter formula: 2A + 2B, where A and B represent the lengths of the parallelogram's sides. This formula emphasizes the importance of adding all sides to determine the complete distance around the shape.
Let's break down the components of the perimeter formula:
- A: Represents the length of one pair of parallel sides
- B: Represents the length of the other pair of parallel sides
- 2A: Accounts for both sides of length A
- 2B: Accounts for both sides of length B
To demonstrate how to calculate the perimeter, let's consider an example. Imagine a parallelogram with side lengths of 6 cm (A) and 4 cm (B). Applying the formula:
Perimeter = 2A + 2B
Perimeter = 2(6 cm) + 2(4 cm)
Perimeter = 12 cm + 8 cm
Perimeter = 20 cm
This example illustrates the process of adding all sides to determine the total perimeter. It's crucial to remember that perimeter is a one-dimensional property, measured in linear units such as centimeters, inches, or meters.
The concept of perimeter relates directly to the one-dimensional property of shapes. Unlike area, which is two-dimensional, perimeter focuses solely on the outer boundary of a figure. This distinction is important when solving real-world problems involving fencing, borders, or any application where the distance around an object is relevant.
When working with parallelograms, it's essential to recognize that opposite sides are always equal in length. This property simplifies the perimeter calculation, as you only need to measure two sides (A and B) to determine the total perimeter. The formula 2A + 2B efficiently captures this characteristic, making it easy to remember and apply.
To further illustrate the concept, consider a real-world scenario. Imagine you're planning to install decorative trim around a parallelogram-shaped window. By measuring the length (A) and width (B) of the window, you can quickly calculate the total amount of trim needed using the perimeter formula. This practical application demonstrates how understanding perimeter can be valuable in everyday situations.
It's worth noting that while the perimeter formula for parallelograms is specific to this shape, the general concept of adding all sides applies to many other geometric figures. For instance, the perimeter of a rectangle is calculated similarly (2L + 2W), and even irregular shapes follow the principle of summing the lengths of all sides.
As you work with perimeter calculations, keep in mind these key points:
- Always use consistent units when adding sides
- Double-check your measurements to ensure accuracy
- Remember that perimeter is a linear measurement, not an area
- Visualize the shape to confirm you've accounted for all sides
Understanding the perimeter formula for parallelograms and its relationship to the one-dimensional property of shapes provides a solid foundation for more advanced geometric concepts. By mastering this fundamental principle, you'll be better equipped to tackle complex problems involving shapes and measurements in both academic and practical settings.
In conclusion, the perimeter formula for parallelograms (2A + 2B) offers a simple yet powerful tool for calculating the distance around these four-sided figures. By emphasizing the importance of adding all sides and recognizing the one-dimensional nature of perimeter, you can confidently approach a wide range of
Area of Parallelograms
Understanding the concept of area is crucial in geometry, especially when dealing with two-dimensional shapes like parallelograms. The area of a parallelogram represents the amount of space covered by this quadrilateral figure on a flat surface. It's a fundamental two-dimensional property that helps us quantify and compare the size of different shapes.
A parallelogram is a four-sided figure with opposite sides parallel to each other. While it may look different from a rectangle, the method for calculating its area is surprisingly similar. The area formula for a parallelogram is:
Area = base * height
This formula might seem familiar because it's identical to the area formula for rectangles. The reason for this similarity lies in the unique properties of parallelograms. Despite their slanted appearance, parallelograms can be transformed into rectangles without changing their area.
To visualize this transformation, imagine cutting off the triangular portion on one end of the parallelogram and moving it to the other side. This rearrangement creates a rectangle with the same base and height as the original parallelogram. This visual demonstration helps explain why the area formulas for these two shapes are the same.
When calculating the area of a parallelogram, it's crucial to use the correct measurements. The base is straightforward it's simply the length of one of the parallel sides. However, the height requires special attention. The height used in the area formula must be the perpendicular height, not the length of the slanted side.
The perpendicular height is the shortest distance between the base and the opposite parallel side. It forms a right angle (90 degrees) with the base. This is different from the slanted side of the parallelogram, which meets the base at an angle other than 90 degrees. Using the slanted side instead of the perpendicular height would result in an incorrect area calculation.
To find the perpendicular height, you can draw a line from any point on the upper parallel side straight down to the base, ensuring it forms a right angle. This line represents the height to be used in the area formula. In some cases, this height line may fall outside the parallelogram itself, but it still represents the correct measurement for area calculations.
Understanding the area of parallelograms has practical applications in various fields. Architects and designers use this knowledge when planning buildings or creating patterns. In landscaping, calculating the area of parallelogram-shaped plots helps in determining the amount of materials needed, such as grass seed or paving stones. Even in everyday life, this concept can be useful when considering flooring or wallpaper for rooms with parallelogram shapes.
The area formula for parallelograms also serves as a stepping stone to understanding more complex shapes. For instance, the area of a triangle can be derived from the parallelogram formula, as a triangle is essentially half of a parallelogram. This interconnectedness of geometric concepts highlights the importance of mastering fundamental shapes like parallelograms.
To practice calculating the area of parallelograms, start with simple examples where the base and height are clearly given. As you become more comfortable, try problems where you need to identify the correct height or where additional steps are required to find the necessary measurements. Remember, the key is always to use the perpendicular height in your calculations.
In conclusion, the area of a parallelogram is a fundamental concept in geometry that builds upon the simpler idea of rectangular area. By understanding how to calculate this space covered using the base and perpendicular height, you gain insight into the properties of two-dimensional shapes and their relationships to one another. This knowledge forms a crucial foundation for more advanced geometric studies and real-world applications in design, construction, and spatial planning.
Comparing Area and Perimeter
When it comes to parallelograms, understanding the difference between area and perimeter calculations is crucial. While both concepts involve measuring aspects of the shape, they serve distinct purposes and require different approaches. The perimeter of a parallelogram is calculated using the lengths of all four sides, including the slanted sides. In contrast, the area calculation utilizes the length of the base and the perpendicular height.
The perimeter uses the slanted sides because it measures the distance around the entire shape. Regardless of the angle or slant of the sides, the perimeter accounts for the actual length of each edge. On the other hand, the area calculation relies on the perpendicular height rather than the slanted side length. This is because area represents the space inside the shape, and the perpendicular height provides the most accurate measure of the parallelogram's vertical extent.
To illustrate the distinction between area and perimeter, consider two parallelograms with the same perimeter but different areas. For example, a parallelogram with a base of 8 units and a height of 4 units might have the same perimeter as another with a base of 6 units and a height of 5 units. However, their areas would differ significantly. Conversely, two parallelograms could have the same area but different perimeters if one has a longer, narrower shape while the other is shorter and wider.
Understanding both area and perimeter is essential in various practical applications. In construction and design, perimeter calculations are vital for determining fencing or bordering needs, while area calculations are crucial for flooring, painting, or land use assessments. In agriculture, farmers might use perimeter measurements for irrigation planning and area calculations for crop yield estimations. The ability to differentiate between these concepts and apply them appropriately can lead to more efficient resource allocation and accurate project planning in numerous fields.
By grasping the nuances of area and perimeter calculations for parallelograms, including the use of slanted sides for perimeter and perpendicular height for area, individuals can make more informed decisions in real-world scenarios. This knowledge enables better problem-solving skills and enhances one's ability to analyze and interpret spatial relationships in both academic and professional contexts.
Special Cases: Rhombus and Square
Parallelograms are versatile quadrilaterals with unique properties, but certain special cases deserve particular attention: the rhombus and the square. These shapes are not only parallelograms but also possess additional characteristics that set them apart.
A rhombus is a parallelogram with four equal sides. This special case maintains all the properties of a parallelogram while introducing new features. In a rhombus, the diagonals bisect each other at right angles, creating four congruent triangles within the shape. The area of a rhombus can be calculated using the formula A = (d1 * d2) / 2, where d1 and d2 are the lengths of the diagonals. This method is often simpler than using the base and height formula of a standard parallelogram.
The perimeter of a rhombus is straightforward to calculate due to its equal sides. If 's' represents the side length, the perimeter is given by P = 4s. This simplification makes rhombus calculations more efficient compared to general parallelograms.
Moving to an even more specialized case, we encounter the square. A square is not only a rhombus but also a rectangle, combining the properties of both. It has four equal sides and four right angles, making it the most symmetrical of all parallelograms. The area of a square is simply A = s², where 's' is the side length. This formula is a simplified version of the parallelogram area formula, as the base and height are equal in a square.
The perimeter calculation for a square follows the same principle as a rhombus: P = 4s. However, squares offer additional simplifications in various geometric problems due to their perfect symmetry and right angles.
These special cases demonstrate how the general properties of parallelograms can be refined and simplified in more specific shapes. While rhombuses and squares maintain the parallel sides and equal opposite angles of parallelograms, their equal sides introduce new relationships and calculation methods. Understanding these special cases not only enriches our knowledge of geometry but also provides efficient tools for solving real-world problems involving these shapes, such as identifying congruent triangles in rhombuses.
Real-World Applications and Practice Problems
Calculating the area and perimeter of parallelograms has numerous real-world applications, particularly in architecture, design, and everyday objects. Understanding these concepts is crucial for professionals and enthusiasts alike.
Applications in Architecture
Architects frequently use parallelogram shapes in building designs. For example, slanted walls or roofs often form parallelograms. Calculating the area is essential for determining material quantities, while perimeter calculations help in estimating fencing or trim requirements.
Design Applications
Graphic designers utilize parallelograms in logos, layouts, and packaging designs. Understanding area calculations helps in determining print sizes or material usage, while perimeter knowledge aids in creating borders or frames.
Everyday Objects
Many everyday items incorporate parallelogram shapes. For instance, some cutting boards, serving trays, or even smartphone screens may have parallelogram forms. Knowing how to calculate their areas and perimeters can be useful for DIY projects or custom fittings.
Practice Problems
To reinforce your understanding, try solving these practice problems:
Beginner Level:
1. A parallelogram has a base of 8 cm and a height of 5 cm. Calculate its area.
2. Find the perimeter of a parallelogram with sides measuring 12 cm and 7 cm.
Intermediate Level:
3. An architect is designing a slanted wall in the shape of a parallelogram. The wall has a base of 15 feet and a height of 10 feet. What is the area of the wall?
4. A designer is creating a logo with a parallelogram shape. If the logo has a perimeter of 40 inches and one side measures 12 inches, what is the length of the other side?
Advanced Level:
5. A parallelogram-shaped garden has an area of 120 square meters and a height of 8 meters. If the perimeter is 56 meters, find the lengths of its sides.
Step-by-Step Solutions
1. Area = base × height = 8 cm × 5 cm = 40 sq cm
2. Perimeter = 2(12 cm + 7 cm) = 2(19 cm) = 38 cm
3. Area = base × height = 15 ft × 10 ft = 150 sq ft
4. Perimeter = 2(12 + x), where x is the unknown side 40 = 2(12 + x) 20 = 12 + x x = 8 inches
5. Let the sides be x and y. Area: xy sin θ = 120 (where θ is the angle between sides) Height: x sin θ = 8 Perimeter: 2(x + y) = 56 Solving these equations: x 16 m, y 12 m
These real-world applications and practice problems demonstrate the importance of understanding parallelogram calculations in various fields. By mastering these concepts, you'll be better equipped to tackle design challenges, architectural problems, and everyday spatial reasoning tasks. Remember, practice is key to improving your problem-solving skills in this area.
Conclusion
In this article, we've explored the essential concepts of area and perimeter in parallelograms. Understanding these key points is crucial for mastering geometry. We began with an introductory video that visually demonstrated these concepts, making them easier to grasp. Remember, the area of a parallelogram is calculated by multiplying its base by its height, while the perimeter is the sum of all four sides. These formulas are fundamental in solving various geometry problem solving. We've seen how parallelograms, despite their unique shape, share similarities with rectangles in terms of area calculation. This knowledge forms a solid foundation for more advanced geometry topics. To truly internalize these concepts, regular practice is vital. We encourage you to solve more problems involving parallelograms and explore related shapes like rhombuses and trapezoids. By doing so, you'll enhance your spatial reasoning and problem-solving skills, essential in many fields beyond mathematics.
Regular practice geometric problems is crucial for mastering these concepts. By engaging in consistent practice, you can improve your understanding and application of geometric principles. This will not only help you in academic settings but also in real-world scenarios where spatial reasoning is required. Additionally, solving geometry problem solving can enhance your analytical skills, making you better equipped to tackle complex problems in various fields. Remember, the key to success in geometry is a solid grasp of the basics and continuous practice.
As you continue to practice geometric problems, you'll find that your confidence and proficiency in the subject will grow. This will enable you to approach more advanced topics with ease and tackle challenging problems with greater efficiency. Keep practicing, stay curious, and never hesitate to seek help when needed. With dedication and effort, you can master the concepts of geometry and apply them effectively in both academic and real-world contexts.
Introduction to Area and Perimeter of Parallelograms: What are the basic properties of a parallelogram?
In this lesson, we'll be learning how to find the area and perimeter for parallelograms. Before diving into calculations, it's essential to understand the basic properties of a parallelogram. This will help us better grasp the concepts of area and perimeter for these shapes.
Step 1: Understanding the Shape
A parallelogram is a 2D shape with four straight sides. In other words, it is a polygon with four sides. This definition might sound familiar because it also describes a rectangle. However, a parallelogram is not a rectangle; it is a slanted version of it. The key difference lies in the angles and the orientation of the sides.
Step 2: Parallel Sides
The term "parallelogram" gives us a hint about one of its fundamental properties: parallel sides. In a parallelogram, each pair of opposite sides is parallel. This means that the top and bottom sides are parallel to each other, and the left and right sides are parallel to each other. Parallel lines are lines that run in the same direction and never intersect, no matter how far they are extended.
Step 3: Equal Lengths of Opposite Sides
Another important property of a parallelogram is that opposite sides are of equal length. This means that the top and bottom sides are the same length, and the left and right sides are also the same length. This property is similar to that of a rectangle, where opposite sides are equal.
Step 4: Angles in a Parallelogram
Unlike a rectangle, the angles inside a parallelogram are not right angles (90 degrees). Instead, the angles are slanted. However, there is a predictable pattern: opposite angles in a parallelogram are equal. This means that if one angle is 60 degrees, the angle directly opposite to it will also be 60 degrees. The sum of the angles in a parallelogram is always 360 degrees.
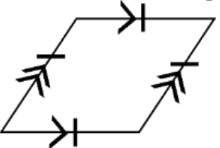
Step 5: Marking Parallel Sides
To visually represent the parallel sides, we use arrow markings. A single arrow on one side and its opposite side indicates that they are parallel. Similarly, a double arrow on the other pair of opposite sides indicates that they are parallel to each other. This helps in easily identifying the pairs of parallel sides in a parallelogram.
Step 6: Special Types of Parallelograms
There are special types of parallelograms, such as the rhombus. A rhombus is a parallelogram where all four sides are of equal length. This is similar to how a square is a special type of rectangle with all sides equal. In a rhombus, the opposite angles are still equal, and the sides are parallel, but all sides are the same length.
Step 7: Dimensions in Geometry
Understanding the dimensions of a parallelogram is crucial for calculating its area and perimeter. A parallelogram is a 2D shape, meaning it has two dimensions: length and width. The perimeter is a 1D property, representing the total distance around the shape. The area is a 2D property, representing the space covered by the shape.
Step 8: Perimeter of a Parallelogram
The perimeter of a parallelogram is calculated by adding the lengths of all four sides. Since opposite sides are equal, the formula for the perimeter is 2 times the sum of the lengths of one pair of opposite sides. If the lengths of the sides are 'a' and 'b', the perimeter P is given by P = 2(a + b).
Step 9: Area of a Parallelogram
The area of a parallelogram is calculated by multiplying the base by the height. The base is one of the sides, and the height is the perpendicular distance between the base and the opposite side. If the base is 'b' and the height is 'h', the area A is given by A = b * h.
Conclusion
Understanding the basic properties of a parallelogram is essential for calculating its area and perimeter. A parallelogram is a 2D shape with four straight sides, where opposite sides are parallel and of equal length. The angles inside a parallelogram are not right angles, but opposite angles are equal. Special types of parallelograms, such as the rhombus, have all sides of equal length. By understanding these properties, we can easily calculate the perimeter and area of parallelograms.
FAQs
-
What is the difference between the area and perimeter of a parallelogram?
The area of a parallelogram represents the space inside the shape and is calculated using the formula: Area = base × height. The perimeter, on the other hand, is the distance around the parallelogram and is calculated by adding all four sides: Perimeter = 2(side A + side B). Area is measured in square units (e.g., cm²), while perimeter is measured in linear units (e.g., cm).
-
How do you find the height of a parallelogram?
The height of a parallelogram is the perpendicular distance between its parallel sides. To find it, draw a line from any point on the upper parallel side straight down to the base, forming a right angle. This line represents the height and is often shorter than the slanted side of the parallelogram.
-
Can a rectangle be considered a parallelogram?
Yes, a rectangle is a special case of a parallelogram. All rectangles are parallelograms because they have two pairs of parallel sides. However, not all parallelograms are rectangles. The key difference is that rectangles have four right angles, while parallelograms can have angles of any measure, as long as opposite angles are equal.
-
How does the area formula for a parallelogram relate to that of a rectangle?
The area formula for both parallelograms and rectangles is the same: Area = base × height. This similarity exists because a parallelogram can be transformed into a rectangle of the same area by moving a triangular portion from one end to the other. This transformation preserves the base and height, explaining why the formulas are identical.
-
What are some real-world applications of parallelogram calculations?
Parallelogram calculations have numerous practical applications. In architecture, they're used for designing slanted walls or roofs. Graphic designers use them in logos and layouts. In agriculture, farmers might use area calculations for crop yield estimations. Construction projects often involve parallelogram shapes for flooring or fencing. Understanding these calculations is also crucial in fields like engineering, interior design, and landscape architecture.
Prerequisite Topics
Understanding the area and perimeter of parallelograms is a crucial concept in geometry, but to fully grasp this topic, it's essential to have a solid foundation in certain prerequisite subjects. Two key areas that play a significant role in comprehending parallelograms are congruence and congruent triangles and the use of right angles in trigonometry.
Let's start with congruence and congruent triangles. This concept is fundamental when working with parallelograms because it helps us understand the properties of opposite sides and angles. In a parallelogram, opposite sides are congruent, and this principle is directly related to the properties of congruent triangles. By understanding how congruent triangles work, students can more easily visualize and prove the characteristics of parallelograms, which is crucial for calculating their area and perimeter.
The study of congruent triangles also introduces important geometric principles such as the Side-Side-Side (SSS) and Angle-Side-Angle (ASA) congruence theorems. These theorems are invaluable when proving properties of parallelograms and can be applied to more complex problems involving area and perimeter calculations.
Moving on to the use of right angles in trigonometry, this concept is particularly important when dealing with the height of a parallelogram. The sine ratio, which is used to calculate angles and sides in right-angled triangles, becomes a powerful tool when determining the height of a parallelogram. This is because the height of a parallelogram is always perpendicular to its base, forming a right angle.
Understanding how to use the sine ratio to calculate angles and sides in right-angled triangles provides students with the necessary skills to find the height of a parallelogram when it's not directly given. This is crucial because the height is a key component in the formula for calculating the area of a parallelogram (Area = base × height).
Moreover, the concepts learned in trigonometry, such as working with angles and ratios, are essential for understanding the relationships between different parts of a parallelogram. This knowledge is not only useful for area calculations but also for solving more complex problems involving parallelograms in real-world applications.
By mastering these prerequisite topics, students build a strong foundation that allows them to approach the study of parallelograms with confidence. The principles of congruence help in understanding the fundamental properties of parallelograms, while trigonometric concepts provide the tools necessary for precise calculations of area and perimeter. Together, these prerequisites form a comprehensive base of knowledge that enables students to tackle more advanced geometric problems and applications involving parallelograms.

