Comparing and ordering numbers up to millions
Topic Notes
In this lesson, we will learn:
- To compare whole numbers up to millions place values by finding the biggest place value of difference
- To order a list of whole numbers up to millions place values by using a place value table
Notes:
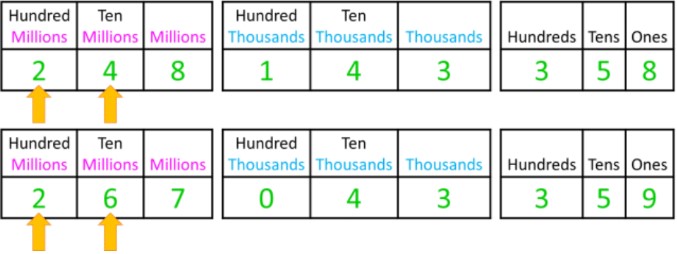
- To compare numbers, look at each place value digit starting on the left (biggest place value)
- Find the biggest place value where the numbers are different to determine which number is bigger or smaller
- Ex. 267,043,359 is bigger than 248,143,358
- When comparing numbers, we use the symbols:

- Ex. 267,043,359 is bigger than 248,143,358
Therefore, 267,043,359 > 248,143,358
- There are two ways to order numbers, from:
- Least to greatest (smallest to biggest)
- Or greatest to least (biggest to smallest)
- One tool to help order a list of numbers is by using a place value table
- Ex. Order the numbers from least to greatest: 12 654, 13 465, 9 546, 11 564

- The place value table allows you to compare all place values clearly.
- 9 546 < 11 564 < 12 654 < 13 465
Introduction to Comparing and Ordering Numbers up to Millions
Welcome to our lesson on comparing whole numbers and ordering whole numbers up to millions! This fundamental skill is crucial for advancing your mathematical abilities. We'll start with an engaging introduction video that will lay the groundwork for understanding these concepts. The video will demonstrate how to compare numbers by looking at their place values, starting from the leftmost digit. You'll learn techniques for quickly determining which number is greater or smaller, and how to arrange multiple numbers in ascending or descending order. We'll explore real-world applications of these skills, making the learning process both practical and fun. By mastering the art of comparing whole numbers and ordering whole numbers up to millions, you'll build a strong foundation for more complex mathematical operations. Remember, this skill is essential for everyday life, from understanding large quantities to making informed decisions. Let's dive in and become number comparison experts together!
Comparing Whole Numbers up to Millions
Understanding Place Value
Before we dive into comparing whole numbers up to millions, it's crucial to understand place value. In our number system, each digit's position determines its value. From right to left, we have ones, tens, hundreds, thousands, ten thousands, hundred thousands, and millions. This knowledge forms the foundation for comparing large numbers effectively.
Step 1: Align the Numbers
When comparing whole numbers, especially large ones, the first step is to align them properly. This means lining up the digits in the same place value columns. For example, when comparing 3,456,789 and 3,654,321, we would align them like this:
3,456,789
3,654,321
Step 2: Compare Digits from Left to Right
Start comparing the digits from left to right, beginning with the highest place value (in this case, millions). If the digits in the millions place are the same, move to the next place value (hundred thousands), and so on. The first place where the digits differ determines which number is greater.
Step 3: Identify the Biggest Place Value of Difference
In our example, the millions place is the same (3), so we move to the hundred thousands place. Here, we see 4 in the first number and 6 in the second. This is the biggest place value of difference. Since 6 is greater than 4, we can conclude that 3,654,321 is greater than 3,456,789.
Using the Math Alligator Concept
The "math alligator" is a fun and memorable way to understand greater than (>) and less than (<) symbols. Imagine these symbols as an alligator's mouth. The alligator always wants to eat the bigger number, so its mouth opens towards the larger value.
For our example:
3,456,789 < 3,654,321
The alligator's mouth (the wider part of the symbol) points towards 3,654,321, indicating it's the larger number.
Examples with Numbers in the Millions
Let's practice comparing large numbers:
1. Compare 5,678,901 and 5,678,910
Aligning the numbers:
5,678,901
5,678,910
The biggest place value of difference is in the ones place. Since 0 < 1, we have:
5,678,901 < 5,678,910
2. Compare 7,123,456 and 7,123,465
Aligning the numbers:
7,123,456
7,123,465
The biggest place value of difference is in the tens place. Since 5 < 6, we have:
7,123,456 < 7,123,465
3. Compare 9,876,543 and 9,876,543
In this case, all digits are identical, so the numbers are equal. We use the equal to (=) symbol:
9,876,543 = 9,876,543
Tips for Comparing Large Numbers
1. Always start with the leftmost digit (highest place value).
2. Use commas or spaces to group digits for easier reading.
3. Remember that zeros at the end of a whole number don't change its value but do affect place value.
4. Practice with various numbers to become comfortable with the process.
Conclusion
Ordering Whole Numbers up to Millions
Understanding how to order whole numbers up to millions is a crucial mathematical skill. This process involves arranging numbers from least to greatest or greatest to least, using place value knowledge. Let's explore this concept in detail.
Least to Greatest
Ordering numbers from least to greatest means arranging them in ascending order. For example, let's order these numbers: 2,456,789; 1,234,567; 3,789,012.
- 1,234,567
- 2,456,789
- 3,789,012
To order these numbers, we compare them digit by digit, starting from the leftmost place value (millions in this case).
Greatest to Least
Conversely, ordering from greatest to least means arranging numbers in descending order. Using the same numbers:
- 3,789,012
- 2,456,789
- 1,234,567
Again, we compare digits from left to right, but this time we put the larger numbers first.
Using a Place Value Table
A place value table for large numbers is an excellent tool for ordering large numbers. Let's use our example numbers:
| Millions | Hundred Thousands | Ten Thousands | Thousands | Hundreds | Tens | Ones |
|---|---|---|---|---|---|---|
| 2 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 3 | 7 | 8 | 9 | 0 | 1 | 2 |
By comparing the digits in each column from left to right, we can easily determine the order.
Visual Aids: Mango and Apple Comparison
To help visualize the concept of ordering, we can use a fruit comparison. Imagine mangoes represent larger numbers and apples smaller ones. When ordering from least to greatest, we'd arrange:
- (1,234,567)
- (2,456,789)
- (3,789,012)
This visual representation helps in understanding that larger numbers (mangoes) come after smaller numbers (apples) in ascending order.
Practice Exercise
Try ordering these numbers from greatest to least: 5,678,901; 4,567,890; 6,789,012.
Solution: 6,789,012; 5,678,901; 4,567,890
Key Points to Remember
- Always start comparing from the leftmost digit (highest place value).
- If the first digits are the same, continue to the next digit until a difference is found.
These key points for ordering numbers will help you accurately arrange numbers in both ascending and descending order.
Practical Applications of Comparing and Ordering Numbers
Comparing and ordering large numbers is a fundamental skill with numerous real-world applications across various fields and everyday life. This ability plays a crucial role in understanding and interpreting data, making informed decisions, and grasping the scale of different phenomena. Let's explore some practical examples where these skills are invaluable.
One of the most common applications is in population statistics. When comparing the populations of different cities, countries, or continents, we often encounter large numbers. For instance, understanding that China's population of approximately 1.4 billion is significantly larger than the United States' 331 million requires the ability to compare and order these figures. This skill is essential for policymakers, urban planners, and demographers who need to make decisions based on population trends and distributions.
In astronomy and space exploration, comparing and ordering large numbers is crucial for comprehending vast cosmic distances. The distance from Earth to the Moon is about 384,400 kilometers, while the distance to Mars varies between 54.6 million to 401 million kilometers, depending on the planets' positions. Scientists and space agencies must accurately compare these distances to plan missions, calculate travel times, and understand the scale of our solar system and beyond.
Financial figures represent another area where these skills are indispensable. In business and economics, comparing and ordering large numbers is essential for analyzing market trends, evaluating company performances, and making investment decisions. For example, when comparing the market capitalization of tech giants like Apple ($2.5 trillion) to smaller companies, investors need to understand the magnitude of these differences to make informed choices.
In environmental science, comparing and ordering large numbers helps us grasp the scale of ecological challenges. For instance, understanding that the Great Pacific Garbage Patch covers an estimated area of 1.6 million square kilometers roughly three times the size of France puts the issue of ocean pollution into perspective. This comprehension is vital for environmental policymakers and activists in their efforts to address such global concerns.
The field of medicine also relies heavily on the ability to compare and order large numbers. When studying disease prevalence, researchers might need to compare infection rates across different populations. For example, understanding that a disease affects 5 out of 100,000 people in one country versus 50 out of 100,000 in another is crucial for allocating resources and developing public health strategies.
In everyday life, these skills come into play when making personal financial decisions. Comparing mortgage rates, understanding tax brackets, or evaluating retirement savings options all require the ability to work with and understand large numbers. For instance, recognizing that a 0.5% difference in mortgage rates can translate to thousands of dollars over the life of a loan is essential for making sound financial choices.
The energy sector provides another example where comparing and ordering large numbers is crucial. When discussing energy production and consumption, we often deal with units like megawatts or terawatt-hours. Understanding that a nuclear power plant might produce 1,000 megawatts while a large wind farm produces 100 megawatts helps in comprehending the scale of different energy sources and their contributions to the power grid.
In conclusion, the ability to compare and order large numbers is not just an academic exercise but a vital skill with wide-ranging applications in our complex world. From population statistics and astronomical distances to financial figures and environmental data, this skill enables us to make sense of the vast amounts of information we encounter daily. It empowers individuals and professionals alike to make informed decisions, understand global phenomena, and contribute meaningfully to various fields of study and practice. As our world becomes increasingly data-driven, the importance of this fundamental mathematical skill in everyday decision-making and professional contexts cannot be overstated.
Common Mistakes and How to Avoid Them
When ordering large numbers, students often encounter several common mistakes. Understanding these errors and learning how to prevent them is crucial for developing strong mathematical skills. One of the most frequent mistakes is overlooking the importance of place value tables, which can lead to significant misunderstandings when dealing with large numbers.
A common error occurs when students focus solely on the number of digits rather than their place value. For example, they might incorrectly assume that 45,678 is larger than 123,456 simply because it has more digits in the ten thousands place. To avoid this mistake, it's essential to emphasize the significance of place value tables and encourage students to start comparing from the leftmost digit.
Another frequent error is misaligning digits when comparing numbers with different digit counts. Students might struggle to compare 9,876 with 54,321 because they don't line up the place values correctly. To prevent this, teaching the use of place value tables can be incredibly helpful. These organizational tools allow students to clearly see each digit's position and make accurate comparisons.
Misreading or miswriting large numbers is also a common issue. For instance, a student might write 300,000 as 30,000, leading to incorrect comparisons. To combat this, encourage students to use commas or spaces to separate thousands, millions, and billions. This simple technique can greatly reduce errors in reading and writing large numbers.
Some students struggle with the concept of zero as a placeholder. They might think that 45,006 is smaller than 45,060 because they overlook the zeros. Teaching the importance of zero in maintaining place value can help avoid this mistake. Emphasize that zeros are crucial in determining a number's magnitude, even if they don't contribute to its value directly.
When ordering large numbers, a common error is not considering all the digits. Students might order 78,901, 78,899, and 78,900 incorrectly if they only look at the first few digits. To prevent this, encourage a systematic approach of comparing each place value from left to right until a difference is found.
The use of number lines for large numbers can be an effective tool in visualizing and comparing large numbers. However, students sometimes make mistakes in scaling when dealing with very large numbers. Teaching proper scaling techniques and the use of benchmarks on number lines can help students avoid this error and better understand the relationships between large numbers.
Another organizational tool that can prevent mistakes is the use of expanded form of numbers. By writing numbers like 45,678 as 40,000 + 5,000 + 600 + 70 + 8, students can more easily see the value of each digit. This method helps in comparing numbers and understanding their composition.
Rounding errors are also common when dealing with large numbers. Students might round 499,999 to 400,000 instead of 500,000. Teaching proper rounding rules and practicing with various numbers can help eliminate this mistake.
Lastly, some students struggle with the concept of inequality symbols (< and >) when comparing large numbers. A helpful tip is to teach the "alligator method," where the open mouth of the alligator always faces the larger number. This visual aid can significantly reduce errors in using these symbols correctly.
By addressing these common mistakes and implementing strategies to avoid them, students can develop a stronger understanding of large numbers. Emphasizing place value, using organizational tools like place value tables and expanded form of numbers, and practicing with diverse examples will help students become more confident and accurate in comparing and ordering large numbers.
Practice Exercises and Self-Assessment
To help students master the skill of comparing and ordering numbers up to millions, here's a comprehensive set of practice exercises with varying difficulty levels. These exercises will allow students to apply their knowledge and self-assess their progress.
Beginner Level Exercises:
- Compare the following pairs of numbers using <, >, or =:
- 45,678 ___ 45,687
- 123,456 ___ 123,465
- 789,012 ___ 789,012
- Order these numbers from least to greatest:
- 234,567 | 234,576 | 234,657 | 234,765
Intermediate Level Exercises:
- Fill in the missing numbers in these sequences:
- 456,789 | 456,799 | _______ | 456,819
- 987,654 | _______ | 987,634 | _______
- Order these numbers from greatest to least:
- 1,234,567 | 1,243,567 | 1,234,657 | 1,243,576
Advanced Level Exercises:
- Compare these numbers and explain your reasoning:
- 3,456,789 and 3,465,789
- 9,876,543 and 9,867,543
- Create a number between 5,678,901 and 5,678,910 that is divisible by 3.
Problem-Solving Exercises:
- The populations of three cities are: City A: 2,345,678; City B: 2,354,678; City C: 2,345,687. Rank the cities from most populous to least populous.
- A company's annual revenue for the past three years was: Year 1: $4,567,890; Year 2: $4,576,890; Year 3: $4,567,980. In which year did the company have the highest revenue?
Self-Assessment Guidance:
To self-assess your understanding and progress, follow these steps:
- Start with the beginner level exercises and gradually move to more advanced ones.
- Time yourself while solving the exercises to track improvement in speed and accuracy.
- Check your answers using a calculator or answer key.
- For each incorrect answer, review the problem and identify where you made a mistake.
- Keep a log of the types of problems you find challenging and focus on practicing those areas.
- Regularly revisit earlier exercises to ensure you maintain your skills.
Remember, consistent practice is key to mastering the skill of comparing and ordering numbers up to millions. As you work through these exercises, pay attention to patterns and relationships between numbers. This will help you develop a deeper understanding of place value and number sense.
If you find yourself struggling with certain types of problems, don't hesitate to seek additional resources or ask for help. Online math forums, educational websites, and your teachers can provide valuable support and explanations.
As you become more comfortable with these exercises, challenge yourself by creating your own problems or finding real-world examples where comparing and ordering large numbers is necessary. This could include analyzing population data, comparing financial figures, or exploring astronomical distances.
Conclusion
In this article, we've explored the fundamental concepts of comparing and ordering numbers. We began with an essential introduction video that laid the groundwork for understanding these crucial mathematical skills. Key points covered include the use of symbols like greater than (>), less than (<), and equal to (=) for number comparison, as well as strategies for ordering numbers from least to greatest and greatest to least. The place value importance in comparing multi-digit numbers was emphasized throughout. We encourage readers to practice these skills regularly, as they form the basis for more advanced mathematical concepts. Remember, the introduction video is a valuable resource for reinforcing these ideas. As you become more comfortable with these basics, consider exploring more advanced number comparison and ordering techniques to further enhance your mathematical prowess. Consistent practice and a willingness to delve deeper into these concepts will undoubtedly strengthen your overall mathematical abilities.
Introduction to Comparing and Ordering Whole Numbers up to Millions
In this guide, we will explore how to compare two large whole numbers up to the millions place values. This involves understanding place values and using comparison techniques to determine which number is larger, smaller, or if they are equal.
Step 1: Understand the Place Values
When comparing large numbers, it's essential to understand the place values. Place values in large numbers include units, tens, hundreds, thousands, ten thousands, hundred thousands, millions, and so on. Each digit in a number has a specific place value, and the value of the digit depends on its position in the number.
Step 2: Start from the Leftmost Digit
To compare two large numbers, begin by looking at the leftmost digit, which is the digit with the highest place value. This is because the leftmost digit represents the largest value in the number. For example, in the number 342, the leftmost digit is 3, which is in the hundreds place.
Step 3: Compare Each Digit in Sequence
Compare the digits of the two numbers starting from the leftmost digit and moving to the right. If the digits are the same, move to the next digit to the right. Continue this process until you find a digit that is different. The number with the larger digit in this place value is the larger number.
Step 4: Example with Smaller Numbers
Let's compare the numbers 342 and 332. Start with the hundreds place:
- Both numbers have 3 in the hundreds place, so they are equal in this place value.
- Move to the tens place: 342 has 4 tens, and 332 has 3 tens. Since 4 is greater than 3, 342 is greater than 332.
Step 5: Example with Larger Numbers
Now, let's compare the numbers 248,143,358 and 267,043,359. Start with the highest place value, which is the hundred millions place:
- Both numbers have 2 in the hundred millions place, so they are equal in this place value.
- Move to the ten millions place: 248,143,358 has 4 ten millions, and 267,043,359 has 6 ten millions. Since 6 is greater than 4, 267,043,359 is greater than 248,143,358.
Step 6: Use Comparison Symbols
When comparing numbers, use the appropriate comparison symbols:
- Less than (<): Indicates that the number on the left is smaller than the number on the right.
- Greater than (>): Indicates that the number on the left is larger than the number on the right.
- Equal to (=): Indicates that both numbers are the same.
For example, 342 > 332 and 248,143,358 < 267,043,359.
Step 7: Practice with More Examples
Practice comparing more pairs of large numbers to become proficient. Remember to always start from the leftmost digit and move to the right, comparing each digit in sequence until you find a difference.
Step 8: Summary
Comparing large whole numbers involves understanding place values and systematically comparing each digit from the leftmost to the rightmost. By following these steps, you can accurately determine which number is larger, smaller, or if they are equal.
FAQs
-
What is the most effective way to compare large numbers?
The most effective way to compare large numbers is to start from the leftmost digit (highest place value) and compare each digit moving right. If the digits are the same, move to the next place value until you find a difference. This method allows for quick and accurate comparisons of numbers, even those with millions of digits.
-
How can I remember which symbol to use when comparing numbers?
A helpful trick is the "alligator method." Imagine the symbols < and > as an alligator's mouth. The alligator always wants to eat the bigger number, so its mouth opens towards the larger value. For example, in 5 < 8, the mouth opens towards 8 because it's larger.
-
Why is place value important when comparing and ordering numbers?
Place value is crucial because it determines the actual value of each digit in a number. When comparing numbers, understanding place value helps you quickly identify which number is larger by looking at the value of digits in corresponding positions. This is especially important for large numbers where small differences in higher place values can significantly affect the number's magnitude.
-
How can I practice ordering numbers effectively?
To practice ordering numbers effectively, start with smaller sets of numbers and gradually increase complexity. Use place value charts to visualize the numbers, create number lines to represent them visually, and practice both ascending and descending orders. Regular practice with varied number sets, including some with close values, will improve your skills over time.
-
What are some real-world applications of comparing and ordering large numbers?
Comparing and ordering large numbers has numerous real-world applications. These skills are used in finance for comparing investments or company revenues, in population studies for analyzing demographic data, in science for understanding astronomical distances or microscopic measurements, and in everyday life for making informed decisions about purchases or understanding statistics in news reports.
Prerequisite Topics
Understanding the foundation of mathematics is crucial when tackling more advanced concepts like comparing and ordering numbers up to millions. Several key prerequisite topics play a vital role in building this understanding, and mastering them will significantly enhance your ability to work with larger numbers.
One of the most fundamental concepts to grasp is place value. Knowing how to use place value tables is essential when dealing with numbers in the millions. This concept helps you understand the significance of each digit's position in a number, which is crucial for comparing and ordering large numbers accurately.
Building on place value, comparing and ordering numbers on a smaller scale is an important stepping stone. Practicing with comparing whole numbers in the hundreds or thousands will prepare you for working with millions. This skill helps you develop strategies for quickly identifying which number is greater or smaller, even when dealing with very large values.
While it may not seem directly related, multiplying fractions and whole numbers can also contribute to your understanding of ordering whole numbers. This skill helps reinforce the concept of magnitude and how numbers relate to each other, which is valuable when comparing numbers in the millions.
Understanding the number systems is another crucial prerequisite. This topic provides a broader context for how numbers work and relate to each other. Familiarity with number lines for large numbers can be particularly helpful when visualizing and comparing numbers up to millions.
Lastly, while it may seem advanced, having some exposure to operations on complex numbers in polar form can provide valuable insights. This topic introduces the concept of the expanded form of numbers, which is incredibly useful when comparing and ordering large numbers. Understanding how to break down numbers into their expanded form can make it much easier to compare their magnitudes.
By mastering these prerequisite topics, you'll build a strong foundation for comparing and ordering numbers up to millions. Each concept contributes to your overall understanding and provides tools and strategies that will make working with large numbers more manageable and intuitive. Remember, mathematics is a cumulative subject, and investing time in these fundamental concepts will pay dividends as you progress to more advanced topics.

