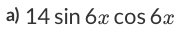Double-angle identities

Using double angle identities in trigonometry

Identities in math shows us equations that are always true. There are many trigonometric identities (Download the Trigonometry identities chart here ), but today we will be focusing on double angle identities, which are named due to the fact that they involve trig functions of double angles such as sin$\theta$, cos2$\theta$, and tan2$\theta$. It's hard to simplify complex trigonometric functions without these formulas.

How to use double angle identities Firstly, what are double angle identities? Let's take a look at the trigonometry identity chart here:

In a way, sine and tangent double angles are very easy because there's only one formula for them. Cosine 2$\theta$ is actually the tricky one because when you see a question, you don't know whether to use the first, the second or the third expression. But don't worry too much because since you have three versions of cosine to choose from, you'll actually be able to make your choice based on what info the problem makes available to you and which one looks the easiest to apply.

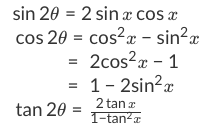
For now, let's take a look at some double angle identities examples. Using the above trig identities cheat sheet, we can go through this trigonometric identities tutorial:

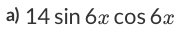
If you look at the trigonometry identity chart, you won't find a number, followed by sine, then cosine—not in quotient identities, not in reciprocal identities, not in Pythagorean identities, and not in sum and difference identities.

You can, however, find this pattern in double angle identities for sine. The sine double angle identity has a number followed by sine, then cosine. Now we know we want to use this formula for this particular question. We have to modify the formula we are given to something we want.

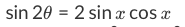
For both formulas we have a sine, cosine, which is nice. But the number in front is of our problems is 14, whereas in the double angle identity, the number in front is 2. What should be our next step? Multiply the whole expression by 7. That will give us 7(sin2$\theta$). Multiplying this into the right side of the equation, we will get:

We are now one step closer to solving the problem. The next thing we have to do to replace theta by 6x.

Let ? = 6x, which gives us:

Isn't this exactly what the original question asked? It turns out that actually equals 7sin(2*6x). You've just completed verifying trig identities through apply double angle identities. This is one example of the many trigonometric identities proofs that can be solved with double angle trig identities.