What is a central angle
Previously, when you worked with angles in a triangle, you were mainly working with central angles. These are angles that had their vertices at the center of the circle. However, in this lesson, we won't be working with central angles.
What is an inscribed angle
If we're not working with central angles, then what angles in a circle will we be focusing on? We'll be tackling inscribed angles.
Inscribed angles are angles that can be anywhere on the circle's circumference. While we're not solely working with central angles anymore, you'll learn that the central angle of a circle will still come into play when we're going through the example problems in this lesson.
Inscribed angle theorem
There are several inscribed angle theorems that we'll be learning today. One of them is the angle in the center theorem. This tells us that an inscribed angle is half of the central angle 2?. This is seen illustrated below.
Angles subtended on the same arc theorem
Another theorem that we'll learn is the angles subtended by the same arc theorem. Given that the endpoints are the same, you'll realize that from the below illustration, it doesn't matter where the inscribed angle is. It will remain the same. As you can also see, this is because they share the same arc (the orange line), hence the name of this theorem.
Question 1:
In the following diagram, the radius is 24 cm and angle BDC is 75°.
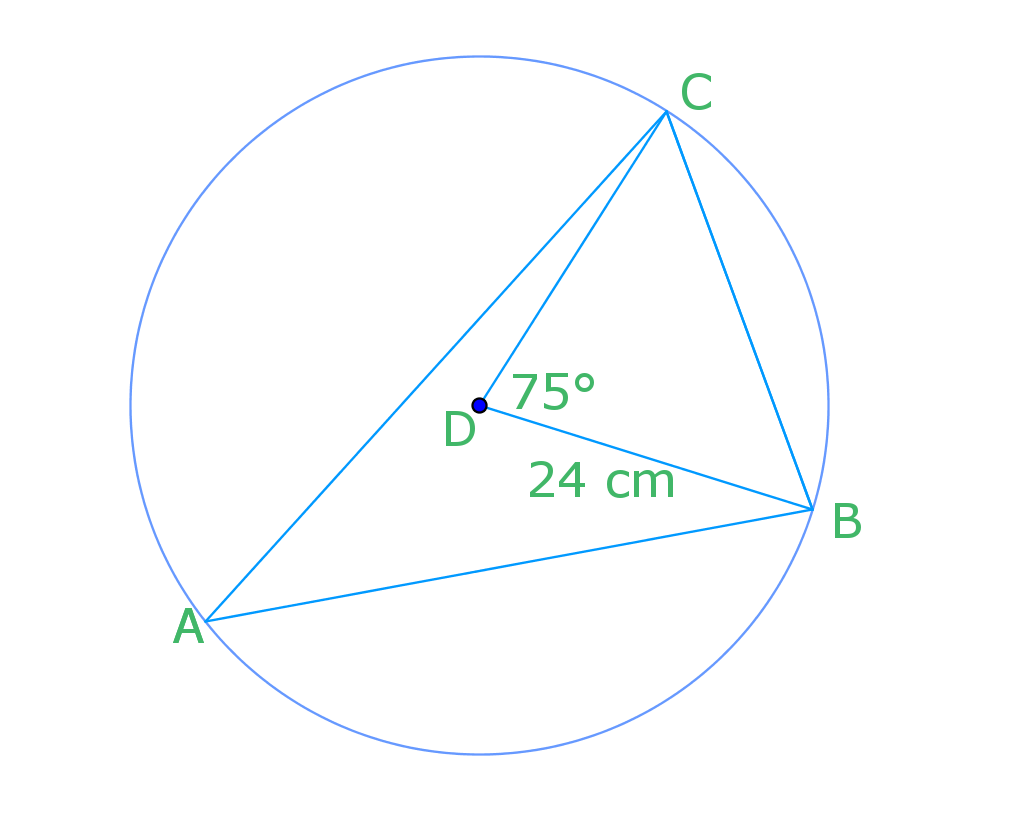
a) Find angle BAC.
Solution:
Angle BDC is the central angle, which equals 75 degrees. Angle BAC is the inscribed angle. According to the inscribed angle theorem, angle BAC equals half of angle BDC. Conversely, you can think about the relationship between angle BDC and angle BAC as the central angle always being doubled that of the inscribed angle.
Central angle = inscribed angle x 2
°
°
b) Find the chord BC
Solution:
Let us draw a bisector in triangle DBC to cut it in half
Now, look at one of the halves cut from triangle DBC
X is half of the chord BC that we are looking for. So solve for x using sin (remember the principles of SohCahToa?)
°
Question 2:
Given angle BAE = 44.5° and angle ADC = 64.27°.
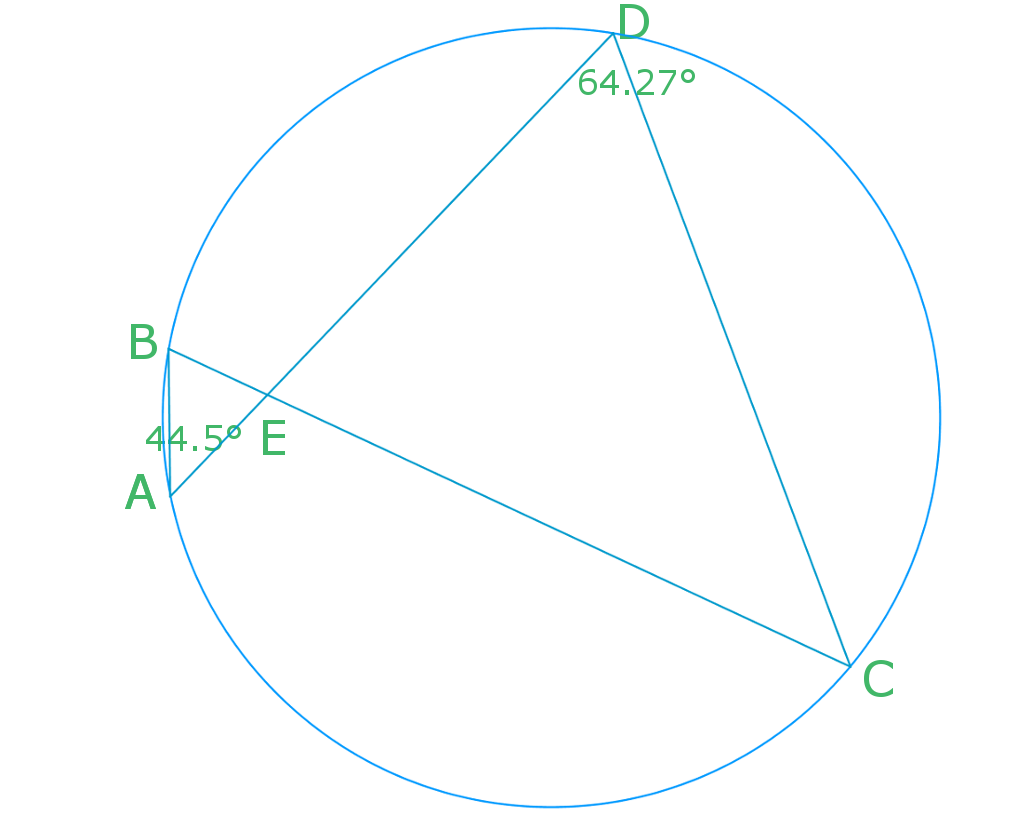
Find angle BCD.
Solution:
Angle BCD and angle BAE are inscribed angles on the same arc. So, angle BCD = BAE = 44.5°. This is based off the angles subtended by the same arc theorem.
Still not sure about the theorems? This online demonstration can show you the proof through you dragging the lines in the circle that form central and inscribed angles.
Next up, you'll be dealing with problems that'll require you to find the arcs of a circle and the area of a sector in circles. You'll also expand on the central and inscribed angles that you learned here, as well as move on to doing proofs on the inscribed angles.






