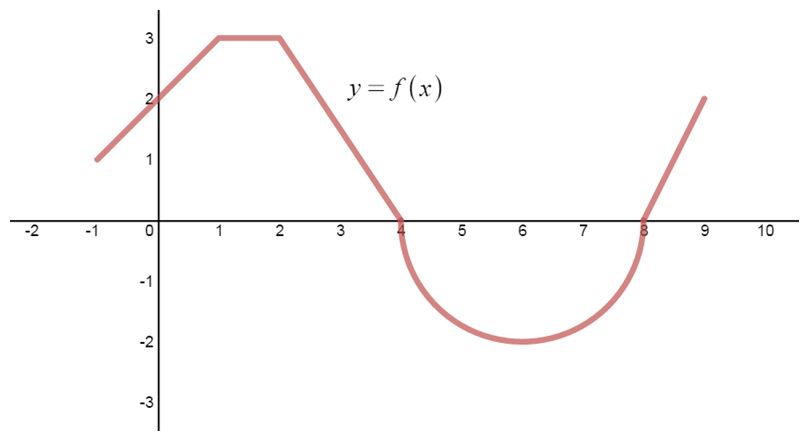
In this section, we will evaluate definite integrals by calculating the area under the curve. We see that the region of integration depends on the lower limit and upper limit of the integral. These areas will be fairly easy to calculate since most of the areas under the curve involve shapes that are familiar to us. We will also notice that curves under the x-axis gives us negative area. Next, we will take a look at questions which involves sketching the curve ourselves, and then determining the area. Lastly, we will take a look at a unique question which involves finding the area of a specific region when given information about two definite integrals.
area under the curve from to