Equivalent fractions
Topic Notes
In this lesson, we will learn:
- How to find equivalent fractions using models
- How to find equivalent fractions using multiplication (and division)
- How to find fractions in lowest terms (simplest form)
Notes:
- Equivalent fractions are fractions with the same value even though they look different (top and bottoms are not the same numbers)
- This can be proven by showing fraction models
- By using the same whole shape and splitting into different numbers of equal parts, all the shape models have the same proportion of shaded area:
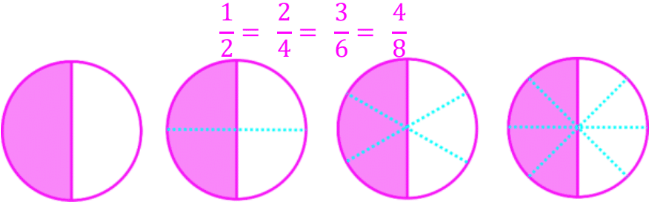
- By lining up number lines on top of each other, all the number line models show the dot representing the fractions on the same point along the line
- Equivalent fractions have the same value because they take the same fraction (proportion) and multiply BOTH the top and bottom by the same number; the value does not change

- Fractions in lowest terms (or simplest form) are the smallest equivalent fraction
- Divide the top and bottom by the same common factor until you cant anymore
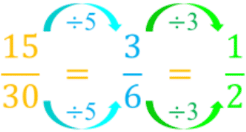
Introduction to Equivalent Fractions
Welcome to the world of equivalent fractions! This fundamental concept in mathematics is crucial for understanding fractions and their relationships. Our introduction video serves as an excellent starting point, providing a clear and engaging explanation of what equivalent fractions are and how to identify them. As you begin this journey, you'll discover that equivalent fractions represent the same value, despite looking different. For example, 1/2 and 2/4 are equivalent fractions. The video will guide you through various examples and methods to create equivalent fractions, such as multiplying or dividing both the numerator and denominator by the same number. Understanding equivalent fractions is essential for comparing, adding, and subtracting fractions with different denominators. As you progress, you'll find that this knowledge forms the foundation for more advanced fraction operations. So, let's dive in and explore the fascinating world of equivalent fractions together!
Understanding Equivalent Fractions
Imagine you're looking at photos of yourself growing up. You might look different in each picture, but you're still the same person inside! That's a lot like equivalent fractions. They may look different on paper, but they represent the same amount. Let's explore this fun concept together!
Think of fractions as slices of a delicious pizza. If we cut a pizza into 2 equal slices and eat 1 slice, we've eaten 1/2 of the pizza. Now, what if we cut the same pizza into 4 slices instead? If we eat 2 slices, we've still eaten half the pizza! So, 1/2 and 2/4 are equivalent fractions they look different, but they're the same amount of pizza.
Let's visualize this with circles:
(Imagine two circles side by side. The first circle is divided into 2 equal parts with one part shaded. The second circle is divided into 4 equal parts with two parts shaded.)
See how both circles have the same amount shaded, even though they're divided differently? That's the magic of equivalent fractions!
Now, let's think about growing up again. When you were 5 years old, you might have said, "I'm 5!" A year later, you'd say, "I'm 6!" These are like different fractions of your life. But what if you said, "I'm 60 months old" instead of "I'm 5"? It sounds different, but it means the same thing!
In fraction language, we can write this as:
5/1 = 60/12
Both fractions represent your age, just expressed differently. This is another example of equivalent fractions.
Let's try another visual:
(Picture three rectangles. The first is divided into 3 parts with 2 shaded. The second into 6 parts with 4 shaded. The third into 9 parts with 6 shaded.)
Can you see how 2/3, 4/6, and 6/9 all show the same amount? They're all equivalent fractions!
Here's a cool trick to find equivalent fractions: multiply or divide both the top (numerator) and bottom (denominator) by the same number. It's like giving a fraction a new outfit it looks different, but it's still the same fraction inside!
For example:
1/2 × 2/2 = 2/4
3/4 × 3/3 = 9/12
Remember, when we multiply or divide both parts by the same number, we're not changing the value of the fraction. We're just expressing it in a different way just like how you're still you whether you're wearing your school uniform or your favorite t-shirt!
Equivalent fractions are super helpful in math. They make it easier to compare fractions, add or subtract them, and even in real-life situations like cooking or sharing things equally.
Next time you see a fraction, try to think of an equivalent one. It's like giving that fraction a friend who looks different but is the same on the inside. The more you practice, the easier it gets!
Remember, fractions are just another way of describing parts of a whole. Whether it's 1/2 of a cookie, 2/4 of a pizza, or 3/6 of a chocolate bar, they're all talking about the same delicious half!
So, don't be intimidated by fractions that look different. They might just be equivalent fractions in disguise! Keep exploring, keep practicing, and soon you'll be a fraction master, able to spot equivalent fractions wherever they hide.
Just like you're growing and changing every day but still remaining wonderfully you, fractions can change their appearance while keeping their true value. Isn't math amazing? Keep up the great work, and remember every fraction has a family of equivalent
Representing Equivalent Fractions on Number Lines
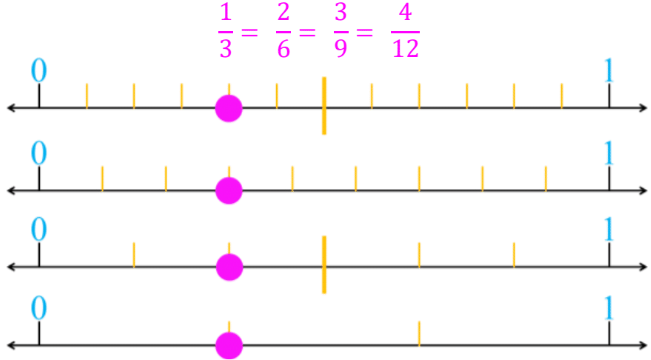
Welcome, young mathematicians! Today, we're going to explore an exciting concept: how to represent equivalent fractions on number lines. Don't worry if it sounds complicated I promise it's actually quite fun and visual! We'll use the example of 1/3, 2/6, 3/9, and 4/12 to guide us through this journey.
First, let's understand what equivalent fractions are. Equivalent fractions are fractions that represent the same amount or proportion, even though they might look different. It's like having different-sized slices of the same pizza the slices may be cut differently, but they still represent the same portion of the whole pizza.
Now, let's visualize this on a number line. Imagine a straight line starting from 0 and ending at 1. This is our playground for today! We'll use this line to show how 1/3, 2/6, 3/9, and 4/12 all land on the exact same spot, despite looking different on paper.
Let's start with 1/3. To find this on our number line, we need to divide the whole line (from 0 to 1) into three equal parts. The first mark after 0 is where 1/3 sits. Go ahead and make a mental note of this spot it's going to be important!
Now, let's look at 2/6. For this, we need to divide our line into six equal parts. Count two of these parts from 0, and voila! You'll find that 2/6 lands exactly where 1/3 did. Isn't that interesting? Despite having different numbers, they're in the same place!
Let's keep going with 3/9. This time, divide the line into nine equal parts. Count three of these tiny parts from 0, and guess what? You're right back at that same spot where 1/3 and 2/6 were!
Finally, let's tackle 4/12. Divide the line into twelve even smaller parts. Count four of these from 0, and... you guessed it! We're back at that same magical spot again.
So, what's happening here? Even though these fractions look different, they all represent the same point on our number line. This is the beauty of equivalent fractions they might be written differently, but they stand for the same proportion of the whole.
Think of it like this: 1/3 means "one out of three parts," 2/6 means "two out of six parts," 3/9 means "three out of nine parts," and 4/12 means "four out of twelve parts." When you simplify these, they all reduce to the same proportion: one-third of the whole.
Using a number line helps us see this concept visually. It's a powerful tool that shows us how fractions relate to each other and to the whole. By placing these equivalent fractions on a number line, we can clearly see that they occupy the same position, reinforcing the idea that they represent the same value.
This visual representation is incredibly helpful in understanding proportion. It shows us that fractions are not just abstract numbers, but real positions on a line. Each equivalent fraction is just a different way of describing the same position or amount.
As you practice more with number lines and equivalent fractions, you'll start to see patterns. For example, you might notice that to get from 1/3 to 2/6, you multiply both the numerator and denominator by 2. To get from 1/3 to 3/9, you multiply by 3, and so on. This is a key principle in working with equivalent fractions.
Remember, math is all about patterns and relationships. By using number lines to explore equivalent fractions, we're uncovering these patterns in a way that's visual and intuitive. It's like solving a puzzle, where each piece helps us see the bigger picture more clearly.
So, the next time you encounter fractions like 1/3, 2/6, 3/9, or 4/12, imagine them on a number line. Picture them all l
Fractions in Lowest Terms
Welcome to the world of fractions in their simplest form! Understanding how to express fractions in their lowest terms is a crucial skill in mathematics. When we talk about fractions in "lowest terms" or "simplest form," we're referring to a fraction that cannot be reduced any further. This means that the numerator (top number) and denominator (bottom number) have no common factors other than 1.
Simplifying fractions is an important process that helps us work with fractions more easily and compare them effectively. The key to simplifying fractions lies in identifying and dividing out common factors from both the numerator and denominator. Don't worry if this sounds challenging at first with practice, you'll become a pro at simplifying fractions!
Let's walk through the process of simplifying fractions step-by-step:
- Identify the common factors of the numerator and denominator.
- Divide both the numerator and denominator by their greatest common factor (GCF).
- Write the new fraction with the reduced numbers.
Let's look at an example to make this clearer. Suppose we want to simplify the fraction 15/30:
- First, let's list the factors of 15 and 30:
- Factors of 15: 1, 3, 5, 15
- Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
- The greatest common factor of 15 and 30 is 15.
- Now, we divide both the numerator and denominator by 15:
- 15 ÷ 15 = 1
- 30 ÷ 15 = 2
- Therefore, 15/30 simplified to its lowest terms is 1/2.
Great job! You've just simplified your first fraction. Let's try another example with larger numbers. How about simplifying 240/400?
- First, let's find the factors of 240 and 400. This might take a bit more time, but don't worry it's good practice for your multiplication skills!
- The greatest common factor of 240 and 400 is 80.
- Now, let's divide both the numerator and denominator by 80:
- 240 ÷ 80 = 3
- 400 ÷ 80 = 5
- Therefore, 240/400 simplified to its lowest terms is 3/5.
Remember, the key to simplifying fractions is practice. Don't be discouraged if it takes some time to spot common factors your skills will improve with each fraction you simplify. Here are some tips to help you along the way:
- Start by looking for small, common factors like 2, 3, or 5.
- If both numbers are even, you can always divide by 2 to start.
- Practice your multiplication tables it will make finding factors much easier!
- Remember that any number divided by itself equals 1, so you can always check if your simplified fraction is correct by dividing the original numerator and denominator by your result.
Simplifying fractions is not just about following rules it's about understanding the relationships between numbers. As you practice, you'll start to see patterns and develop a intuition for working with fractions. This skill will be invaluable as you progress in mathematics, especially when you start working with more complex fraction operations like addition, subtraction
Methods for Finding Equivalent Fractions
Welcome, math enthusiasts! Today, we're diving into the exciting world of equivalent fractions. Don't worry if it sounds challenging we'll explore fun and easy methods to master this concept together!
Equivalent fractions are fractions that represent the same value, even though they may look different. Let's discover how to find them using multiplication and division.
Multiplication Method
One of the simplest ways to find equivalent fractions is by multiplying both the numerator and denominator by the same number. For example, let's start with the fraction 1/2:
- 1/2 × 2/2 = 2/4
- 1/2 × 3/3 = 3/6
- 1/2 × 4/4 = 4/8
See how easy that was? All these fractions (1/2, 2/4, 3/6, 4/8) are equivalent!
Division Method
We can also use division to find equivalent fractions. This method is particularly useful when simplifying fractions. For instance, let's simplify 8/12:
- 8 ÷ 4 = 2, 12 ÷ 4 = 3, so 8/12 = 2/3
Both 8/12 and 2/3 are equivalent fractions!
Checking for Equivalence
To check if two fractions are equivalent, you can use cross-multiplication. Multiply the numerator of the first fraction by the denominator of the second, and vice versa. If the results are equal, the fractions are equivalent. For example:
Are 2/3 and 4/6 equivalent?
- 2 × 6 = 12
- 3 × 4 = 12
Since both results are 12, these fractions are indeed equivalent!
Practice Problems
Ready to put your skills to the test? Try these practice problems:
- Find three equivalent fractions for 3/4 using the multiplication method.
- Simplify 15/25 using the division method.
- Check if 5/8 and 15/24 are equivalent using cross-multiplication.
Remember, there's no single "right" way to find equivalent fractions. Feel free to experiment with both multiplication and division methods to see which works best for you. The more you practice, the more comfortable you'll become with these techniques.
Don't get discouraged if you don't get it right away learning math is a journey, and every step forward is progress! Keep practicing, and soon you'll be an equivalent fractions expert.
As you work on these problems, try to visualize the fractions. It can be helpful to draw them out or use fraction manipulatives if you have them. This can make the concept more concrete and easier to understand.
Remember, equivalent fractions are all around us in everyday life. When you're sharing a pizza or dividing a chocolate bar, you're working with equivalent fractions without even realizing it!
Keep up the great work, and don't hesitate to ask for help if you need it. Math is all about exploration and discovery, so enjoy the process of learning about equivalent fractions. You've got this!
Real-World Applications of Equivalent Fractions
Equivalent fractions might seem like a purely mathematical concept, but they play a crucial role in our everyday lives. Understanding how to work with equivalent fractions can make many real-world tasks easier and more efficient. Let's explore some practical scenarios where this knowledge comes in handy.
In the kitchen, equivalent fractions are a cook's best friend. Imagine you're baking your favorite chocolate chip cookies, but the recipe makes 24 cookies and you only want to make 12. You'll need to halve all the ingredients. This is where equivalent fractions shine! If the recipe calls for 3/4 cup of sugar, you'll use 3/8 cup (which is equivalent to half of 3/4). Similarly, 1/2 cup of butter becomes 1/4 cup. By understanding equivalent fractions, you can easily scale recipes up or down to suit your needs.
Measurement is another area where equivalent fractions are invaluable. Let's say you're helping your parents with a home improvement project, and you need to measure 3/8 of an inch on a piece of wood. But your ruler only shows 1/4 inch markings. No problem! You know that 3/8 is equivalent to 6/16, so you can easily find the midpoint between 1/4 (4/16) and 1/2 (8/16) on your ruler. This skill is especially useful in carpentry, sewing, and other crafts where precise measurements are crucial.
Sharing is perhaps one of the most relatable scenarios for students to understand equivalent fractions. Imagine you have a pizza cut into 8 slices, and you want to share it equally among 4 friends. Each friend would get 2/8 of the pizza, which is equivalent to 1/4. If you had cut the pizza into 16 slices instead, each friend would get 4/16, which is also equivalent to 1/4. This demonstrates how different fractions can represent the same portion, making fair sharing easier to understand and implement.
In sports and fitness, equivalent fractions help athletes and coaches track progress and set goals. A runner might aim to complete a mile in 6 minutes, which is equivalent to running a quarter-mile in 1 minute and 30 seconds, or 90 seconds. Understanding these equivalences allows for more flexible training regimens and more accurate performance measurements.
By recognizing the practical applications of equivalent fractions in cooking, measurement, sharing, and various other daily activities, students can better appreciate the importance of this mathematical concept. It's not just about solving problems on paper; it's about making informed decisions, being precise in our actions, and fairly distributing resources in real-life situations. Mastering equivalent fractions empowers us to navigate these everyday scenarios with confidence and accuracy.
Conclusion
Equivalent fractions are a fundamental concept in mathematics, representing the same value using different numerators and denominators. As we've explored in the introduction video, these fractions are created by multiplying or dividing both the numerator and denominator by the same non-zero number. This key principle allows us to simplify, compare, and perform operations with fractions more easily. Remember, the video provides a solid foundation for understanding equivalent fractions, so don't hesitate to revisit it if needed. To truly master this concept, practice is essential. Challenge yourself with various exercises, from identifying equivalent fractions to creating your own. As you become more comfortable, explore how equivalent fractions apply to real-world situations. This knowledge will serve as a stepping stone to more advanced mathematical concepts. Embrace the learning process, and don't be afraid to ask questions. Your journey with equivalent fractions is just beginning, and there's so much more to discover!
Introduction to Equivalent Fractions
What are equivalent fractions?
Step 1: Understanding the Concept of Equivalent Fractions
Equivalent fractions are fractions that may look different but represent the same value. This means that even though the numerators (top numbers) and denominators (bottom numbers) of these fractions are different, the fractions themselves are equal in value. For example, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions because they all represent the same portion of a whole.
Step 2: Using an Analogy to Explain Equivalent Fractions
To better understand how fractions can look different but still be the same, think of a person growing up. A person looks different as they age from a baby to a child, teenager, adult, and senior. Despite these changes in appearance, they are still the same person. Similarly, equivalent fractions may look different due to different numerators and denominators, but they represent the same value.
Step 3: Visualizing Equivalent Fractions with Models
One way to visualize equivalent fractions is by using fraction models. For instance, consider a circle divided into two parts, with one part shaded. This represents the fraction 1/2. If we divide the same circle into four parts and shade two of them, we get the fraction 2/4. Although the number of parts has changed, the shaded area remains the same, demonstrating that 1/2 and 2/4 are equivalent.
Step 4: Creating More Equivalent Fractions
We can continue this process to create more equivalent fractions. For example, if we divide the circle into six parts and shade three of them, we get the fraction 3/6. Similarly, dividing the circle into eight parts and shading four of them gives us the fraction 4/8. In each case, the shaded area remains the same, showing that 1/2, 2/4, 3/6, and 4/8 are all equivalent.
Step 5: Using Number Lines to Represent Equivalent Fractions
Another way to represent equivalent fractions is by using number lines. For example, if we have a number line from 0 to 1 and divide it into three equal parts, the point at 1/3 represents one-third of the distance from 0 to 1. If we divide another number line into six equal parts, the point at 2/6 will line up with the point at 1/3, showing that 1/3 and 2/6 are equivalent.
Step 6: Comparing Multiple Equivalent Fractions on Number Lines
We can extend this method to compare more equivalent fractions. For instance, dividing a number line into nine parts and marking the point at 3/9 will align with the points at 1/3 and 2/6. Similarly, dividing a number line into twelve parts and marking the point at 4/12 will also align with these points. This demonstrates that 1/3, 2/6, 3/9, and 4/12 are all equivalent fractions.
Step 7: Understanding the Proportional Relationship
The key to understanding equivalent fractions is recognizing that they all represent the same proportion of a whole. Whether we divide a shape or a number line into different numbers of parts, as long as the proportion of the shaded or marked parts remains the same, the fractions are equivalent. This proportional relationship is what makes fractions like 1/2, 2/4, 3/6, and 4/8 equivalent.
Step 8: Practical Applications of Equivalent Fractions
Understanding equivalent fractions is important in many real-life situations, such as cooking, measuring, and dividing resources. For example, if a recipe calls for 1/2 cup of an ingredient, you can use 2/4 cup or 3/6 cup if those measurements are more convenient. Recognizing equivalent fractions helps ensure accuracy and flexibility in various tasks.
FAQs
Here are some frequently asked questions about equivalent fractions:
-
What are equivalent fractions?
Equivalent fractions are fractions that represent the same value or proportion, even though they may look different. For example, 1/2, 2/4, and 3/6 are all equivalent fractions because they represent the same amount.
-
How do you find equivalent fractions?
You can find equivalent fractions by multiplying or dividing both the numerator and denominator by the same non-zero number. For instance, to find an equivalent fraction for 1/3, you can multiply both the numerator and denominator by 2, resulting in 2/6.
-
Why are equivalent fractions important?
Equivalent fractions are crucial for comparing, adding, and subtracting fractions with different denominators. They also help in simplifying fractions and understanding proportions in real-world applications like cooking, measurement, and sharing.
-
How can I check if two fractions are equivalent?
You can check if two fractions are equivalent by cross-multiplying. Multiply the numerator of the first fraction by the denominator of the second, and vice versa. If the results are equal, the fractions are equivalent. For example, to check if 2/3 and 4/6 are equivalent: 2 × 6 = 12 and 3 × 4 = 12, so they are equivalent.
-
Can equivalent fractions be used in everyday life?
Yes, equivalent fractions have many practical applications. They are used in cooking to adjust recipe quantities, in measurement for precise calculations, in sharing to ensure fair distribution, and in sports and fitness to track performance and set goals.
Prerequisite Topics
Understanding equivalent fractions is a fundamental concept in mathematics that builds upon several basic mathematical principles. While there are no specific prerequisite topics listed for this subject, it's important to recognize that a solid foundation in basic arithmetic and fraction concepts is essential for grasping equivalent fractions fully.
To truly comprehend equivalent fractions, students should have a good grasp of basic fraction concepts. This includes understanding what fractions represent, how they are written, and how they relate to parts of a whole. Familiarity with numerators and denominators is crucial, as these components play a vital role in creating and identifying equivalent fractions.
Additionally, a strong foundation in multiplication and division is necessary. These operations are fundamental when working with equivalent fractions, as they are used to create equivalent fractions by multiplying or dividing both the numerator and denominator by the same number. Without a solid understanding of these basic arithmetic operations, students may struggle to generate or recognize equivalent fractions accurately.
Another important aspect is the concept of proportional reasoning. This skill helps students understand that equivalent fractions represent the same portion of a whole, despite having different numerators and denominators. Developing this intuitive sense of proportion is crucial for working with equivalent fractions in various mathematical and real-world contexts.
Furthermore, a basic understanding of simplification and reducing fractions to their lowest terms is beneficial. This knowledge helps students recognize when fractions are equivalent, even if they're not written in the same form. It also aids in simplifying complex fraction problems and in comparing fractions effectively.
While not always explicitly stated as prerequisites, skills in visual representation and pattern recognition can greatly enhance a student's ability to work with equivalent fractions. Being able to visualize fractions using diagrams or number lines can provide a concrete understanding of how different fractions can represent the same value.
Lastly, a general comfort with numbers and number sense is invaluable. This includes understanding the relationships between numbers, estimating, and having a feel for numerical values. Such number sense allows students to approach equivalent fractions with confidence and intuition.
In conclusion, while there may not be a specific list of prerequisite topics for equivalent fractions, a strong foundation in basic arithmetic, fraction concepts, and mathematical reasoning is crucial. These fundamental skills provide the necessary groundwork for students to explore, understand, and apply the concept of equivalent fractions effectively in their mathematical journey.

