ASTC rule in trigonometry (All Students Take Calculus)
Examples
Lessons
Free to Join!
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Trigonometry ASTC
When you work with trigonometry, you'll be dealing with four quadrants of a graph. The x and y axis divides up a coordinate plane into four separate sections.
ASTC is a memory-aid for memorizing whether a trigonometric ratio is positive or negative in each quadrant: [Add-Sugar-To-Coffee]
When you draw it out, it looks like this:
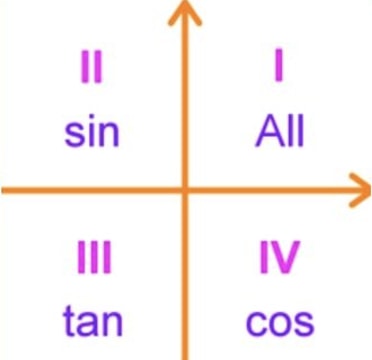
You can even use this diagram as a trigonometry cheat sheet. ASTC will help you remember how to reconstruct this diagram so you can use it when you're met with trigonometry quadrants in your test questions.
In the above graphic, we have quadrant 1 2 3 4. In quadrant 1, both x and y are positive in value. In quadrant 2, x is negative while y is still positive. In quadrant 3, both x and y are negative. Lastly, in quadrant 4, x is positive while y is negative.
What this tells us is that if we have a triangle in quadrant one, sine, cosine and tangent will all be positive. In quadrant two, only sine will be positive while cosine and tangent will be negative. See how this is an easy way to allow you to remember which trigonometric ratios will be positive?
If you don't like Add Sugar To Coffee, there's other acronyms you can use such as:
All Stations To Central
Better yet, if you can come up with an acronym that works best for you, feel free to use it. As long as it contains ASTC in that order, you'll remember the trig quadrants.
If you wanted to look further into trigonometric ratios, why not take a look and revise how the sine graph is graphed. You can also see how the cosine and tangent graphs look and what information you can get out of them.
What about the reciprocals of each trig function?
Recall that each of the three core trig functions have reciprocal identities. While these reciprocal identities are often used in solving and proving trig identities , it is important to see how they may fit in the grand scheme of the "All Students Take Calculus" rule
Most often than not, you will be provided with a "cheat sheet", a sin cos tan chart outlining all the various trig identities associated with each of these core trigonometric functions. However, committing these reciprocal identities to memory should come naturally with the help of the memory aid discussed earlier above.

Looking at each reciprocal identity we can see that
■ cscθ is the reciprocal of sinθ■ secθ is the reciprocal of cosθ
■ cotθ is the reciprocal of tanθ
Now how does this apply to our 4 quadrants?
We now observe that in quadrant two, both sine and cosecant are positive. So if there was a triangle in quandrant two, only the trigonometric ratios of sine and cosecant will be positive. Moving on to quadrant three, we now see that both tan functions and cotangent trig functions are positive here. Likewise, a triangle in this quadrant will only have positive trigonometric ratios if they are cotangent or tangent. In quadrant four, the only trig ratios that will be positive are secant and cosecant trig functions.
If you feel like you need to create a new mnemonic memory device (Mnemonic device definition: a procedure that is used to jog one's memory or help commit information to memory) to help you remember which reciprocal trig identities are positive and/or what corresponding trig function they are related to, try one of the following:
■ All Cougars Creep Silently
■ All Children Cry Savagely
■ All Circuits Create Signals
Feel free to create your own menmonic memory aid for these reciprocal trig functions. Whichever one helps triggers your memory most effectively and efficiently is the best one for you.
How does "all students take calculus" work?
"All students take calculus" (i.e. ASTC) is a mnemonic device that serves to help you evaluate trigonometric ratios. Unlike your standard trigonometry formula that may rely on brute memorization, a mnemonic device, or memory aid, is a lot more helpful as a tool to help you recollect easily and efficiently. Mnemonics in trigonometry is quite common given the sheer amount of trig identities there are. One example you might recall from your right triangle trigonometry is SOH-CAH-TOA.
Since trigonometric ratios can fall into any of the four graph quadrants, we can use our mnemonic device to determine when trigonmetric trigonometric ratios are going to positive or negative. That is the sole use and purpose of ASTC.
From then on, problems will require further simplification to produce trigonometry values that are exact (i.e. when dealing with special triangles). Some problems will yield results that can only be simplified to trig ratios or decimal answers.
Knowing the relationship between ASTC and the four trig quadrants will also be helpful in the next lesson when we explore positive and negative unit circle values.
Walk through examples and practice with ASTC
As aforementioned, the fundamental purpose of ASTC is to help you determine whether the trigonometric ratio under evaluation is positive or negative.
Here are a few questions you want to ask yourself before you tackle your problem:
1. What quadrant is it in?
2. What is positive in this quadrant?
3. What is negative in this quadrant?
Example 1: Determine if the following trigonometric function will have a positive or negative value: Sin 75°
Step 1: Determine what quadrant it is in – Looking at the image below, we see that when when θ is between 0° and 90°, we will be in quadrant 1. Since 75° is between the limts of 0° and 90°, we can affirm that the trig ratio we are examining is in quadrant 1.
Step 2: In quadrant 2, we are now looking at the second letter of our memory aid acronym ASTC. This tells us immediately that only sine functions (and it's reciprocal) will be positive.
Step 3: Since this is quadrant 1, nothing is negative in here.
We can therefore confirm that the value of Sin 75° will be positive
Example 2: Determine if the following trigonometric function will have a positive or negative value: tan 175°
Step 1: Since θ is now greater than 90° but less than 180°, we are now in quadrant 2.
Step 2: In quadrant 2, we are now looking at the second letter of our memory aid acronym ASTC. This tells us immediately that only sine functions (and it's reciprocal) will be positive.
Step 3: In quadrant 2, tangent and cosine functions are negative along with their reciprocals.
Therefore, we can say the value of tan 175° will be negative.
Example 3. Determine if sec 300° will have a positive or negative value:
Step 1: Since θ is greater than 270°, we are now based in quadrant 4.
Step 2: Recall that secant is the reciprocal of cosine. Going back to our memory aid, specifically the fourth letter in our acronym, ASTC, we see that cosine is positive in quadrant 4.
Step 3: In quadrant four, sine, tangent and their reciprocals are negative.
Therefore, we can conclude that sec 300° will have a positive value.
What about negative angles?
Some trigonometric questions you encounter will involve negative angles. How do we reconcile problems like this?
Let's begin by going back to looking at angles on a cartesian plane: Taking a closer look at the four qudrants of a graph on a cartesian plane, we can observe angles are formed by revolutions around the axes of the cartesian plane. Each revolution in the anti-clockwise direction equates to 360° while each revolution in the clockwise direction is equal to -360 °. In conjunction with our memory aid, ASTC, we can then extrapolate information on whether a trig value is negative or positive based on what circle quadrants the trig ratios fall into.
Walk through examples of negative angles
Example 1. Determine if cot (-160°) will have a positive or negative value:
Step 1. Going in the clockwise direction, we see that this places us in quadrant 3 as θ is between -90° and -180°.
Step 2. In this quadrant we know that only tangent and its reciprocal, cotangent, are positive – ASTC.
Step 3. All other trig functions are negative, including sine, cosine and their reciprocals.
Therefore the value of cot (-160°) will be positive.
Example 2. Determine if csc (-45°) will have a positive or negative value:
Step 1. Once again, since we are dealing with a negative degree value, we move in the clockwise direction starting from x-axis in quadrant 1. Since θ is between 0° and -90°, we know we are in quadrant 4.
Step 2. In quadrant 4, only cosine and its reciprocal, secant, are positive (ASTC).
Step 3. In quadrant 4, sine, tangent, and their reciprocals are negative. In this scenario we are dealing with the reciprocal of reciprocal of sine – csc.
csc (-45°) will therefore have a negative value.
Solving more complex trigonometric ratios with ASTC
Moving beyond negative and positive angles, we can be faced with more complex trigonometric equations to evaluate.
Some of the common examples include the following:
■ (360° - θ)■ (270° + θ), (270° - θ)
■ (180° + θ), (180° - θ)
■ (90° + θ) or (90° - θ)
Step 1. The first step in solving ratios with these values involves identifying which quadrant they fall in. Based on the operator in each equation, this should be straightforward:
Step 2. The next step involves a conversion to an alternative trig function. Be careful as this only applies to angles involving 90° and 270°. Here are the rules of conversion:
■ tan θ = cot θ■ tan θ = cot θ
■ tan θ = cot θ
Step 3. Use our memory aid ASTC to determine if the value will be negative or positive, and then simplify the trigonometric function.
Example 1. Evaluate sin (270° - θ).
Step 1. Looking back at our graph of quadrants and revolutions, we see that (270° - θ) falls into quadrant 3.
Step 2. Since we are dealing with the value of 270°, we have to convert the trig identity as per the rules outlined above. Sin θ becomes cos θ.
Step 3. In quadrant 3, only tangent and cotangent are positive based on ASTC. Sine in quadrant 3 is negative, therefore we have to make sure that our newly converted trig function is also negative (i.e. cos θ).
Our final answer is as follows: sin (270° - θ) = - cos θ.
Example 2. Evaluate cos (90° + θ).
Step 1. Notice that 90° + θ is in quadrant 2 (see graph of quadrants above).
Step 2. Also notice that since we are dealing with 90°, we have to convert the cosine function to sine based on the rules of conversion listed above.
Step 3. In quadrant 2, sine and cosecant are both positive based on our handy ASTC memory aid. Everything else – tangent, cotangent, cosine and secant are negative. Therefore we have to ensure our newly converted trig function is also negative.
Our final answer is as follows: cos (90° + θ) = - sin θ.
What if the angles are greater than or equal to 360°
The steps for these kinds of problems are largely the same but involve one additional, initial step.
When we are faced with angles that are greater than or equal to 360, we first divide by 360 and then take the remainder of that division as the new value when solving the trig ratio.
Example 1. Evaluate sin 870°.
Step 1. Divide 870 by 360 and find the remainder
The remainder in this scenario is 150. So we take this remainder as our new value in our trig ratio: sin 150°.
Step 2. Observe that we are in quadrant 2. In quadrant 2, Sine and cosecant are positive (ASTC).
Step 3. Simplify Sin 150°:
Recall that sin (180° - θ) is in quadrant 2. In quadrant 2, Sine is positive. Also recall that we do not have to convert here because we are dealing with 180°.
Using our 30-60-90 special right triangle we can get an exact answer for sin 30°:
Example 2. Evaluate sin 735°.
Step 1. Divide 735 by 360 and retrieve the remainder.
Use the remainder in place of the original value – sin 735° = sin 15°.
Step 2. Observe that we are in quadrant 1. In quadrant one, all things are positive (ASTC).
Step 3. Simplify – In this scenario we can leave our answer as sin 15° instead of a decimal value.
If we were asked how to simplify sin 15° without a calculator, we would need to apply sum and difference trig identities which we'll learn in a future lesson.
Basic Concepts
Related Concepts
remaining today
remaining today



