Least-squares problem
Everything You Need in One PlaceHomework problems? Exam preparation? Trying to grasp a concept or just brushing up the basics? Our extensive help & practice library have got you covered. | Learn and Practise With EaseOur proven video lessons ease you through problems quickly, and you get tonnes of friendly practise on questions that trip students up on tests and finals. | Instant and Unlimited HelpOur personalized learning platform enables you to instantly find the exact walkthrough to your specific type of question. Activate unlimited help now! |
Make math click 🤔 and get better grades! 💯Join for Free
0/3
Intros
Lessons
- Least Squares Problem Overview:
- The Least Squares Solution
• Ax=b give no solution
• Approximate closest solution x^
• The least Squares Solution x^=(ATA)−1ATb
• Not always a unique solution - The Least Squares Error
• Finding the error of the solution x^
• Use the formula ∥b−Ax^∥ - Alternative Calculation to Least-Squares Solutions
• Orthogonal columns of A→Ax^=b^
• QR factorization A=QR→Rx^=QTb
0/5
Examples
Lessons
- Finding the Least Squares Solutions with ATAx^=ATb
Find a least-squares solution of Ax=b if
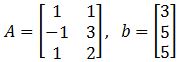
- Describe all least-squares solutions of equation Ax=b if
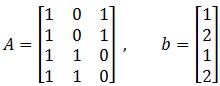
- Finding the Least Squares Error
You are given that the least-squares solution of Ax=b is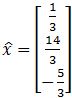 . Compute the least-square error if
. Compute the least-square error if
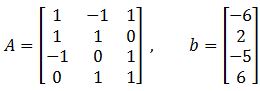
- Finding the Least Squares Solutions with Alternative Ways
Find the orthogonal projections of b onto the columns of A and find a least-squares solution of Ax=b.
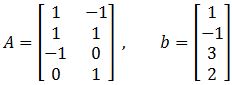
- Use the factorization A=QR to find the least-squares solution of Ax=b
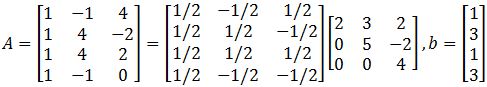
Free to Join!
StudyPug is a learning help platform covering maths and science from primary all the way to second year university. Our video tutorials, unlimited practice problems, and step-by-step explanations provide you or your child with all the help you need to master concepts. On top of that, it's fun — with achievements, customizable avatars, and awards to keep you motivated.
Easily See Your Progress
 We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
We track the progress you've made on a topic so you know what you've done. From the course view you can easily see what topics have what and the progress you've made on them. Fill the rings to completely master that section or mouse over the icon to see more details.Make Use of Our Learning Aids
Earn Achievements as You Learn
 Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.Create and Customize Your Avatar
 Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Topic Notes
Least-squares problem
Method of least squares
In linear algebra, we have talked about the matrix equation Ax=b and the unique solutions that can be obtained for the vector x, but, sometimes Ax=b does not have a solution, and so, for those cases our best approach is to approximate as much as possible a value for x.
Therefore, the topic for the lesson of today is a technique dedicated to obtain that close-enough solution. The technique has been called least-squares and is based on the principle that since we cannot obtain the solution of the vector x for the matrix equation Ax=b, then we have to find an x that produces a multiplication Ax as close as possible to the vector b
If A is an m×n matrix and b is a vector in Rn, then the least-squares solution for Ax=b is the vector xin Rn where the following condition applies for all x in Rn:
This means that if we cannot obtain a solution for the equation Ax=b, then our best approximation to the true value of x, which we call x or the least-squares solution (also called the least squares approximation), can be obtained if the condition in equation 1 is met. The left hand side on this equation is what we call the magnitude of the smallest possible error of the best approximation to the vector x, in other words, is the smallest possible error in x. The right hand side is the smallest possible error in x.
Having seen how the method of least squares is related to errors, we can talk about how this relates to a real life scenario. Basically, the idea of the least square method is that as much as we want to be accurate while performing measurements during studies or experiments, the truth is that there is just so much precision we can obtain as humans with non-perfect tools in a non-perfect world. From the scale of the measurements, to random changes in the environment, etc. There will be scenarios in which our measurements are not good enough and for that we have to come up with a solution that approximates as much as possible to the true value of the element we are measuring. This is where the least-squares solution brings a way to find a value that otherwise is unattainable (and actually, this is just the best approximation we can have but not the real value itself).
Least squares solution
Having a m×n matrix A and column vector b in Rn, using the next matrix equation for the relationship of the unit vector x and the matrix A and its transpose:
We can solve for the unit vector x^ and we have that:
This is what is called the least-squares solution of a matrix equation Ax=b
The steps to obtain the least-squares solution x^ for a problem where you are provided with the matrix A and the vector b are as follows:
- If you follow the matrix equation found in equation 2:
- Find the transpose of vector A:AT
- Multiply AT times matrix A, to obtain a new matrix: ATA
- Multiply the transpose of matrix A with the vector b
- Construct the matrix equation ATAx^=ATb using the results from steps b and c
- Transform the matrix equation above into an augmented matrix
- Row reduce the augmented matrix into its echelon form to find the components of vector x^
- Construct the least squares solution x^ with the components found.
- If you follow the formula for x^ that is found in equation 3:
- Start by obtaining the transpose of matrix A:AT
- Multiply AT times matrix A, to obtain a new matrix: ATA
- Find the inverse of matrix ATA
- Multiply the transpose of matrix A with the vector b
- Multiply the results you obtained in steps 4 and 5 together to obtain: x^=(ATA)−1ATb
There are also some alternative calculations in order to find the least-square solution of a matrix equation. For example: let A be a mxn matrix where a1,a2,...,an are the columns of A. If Col(A)={a1,a2,...,an} form an orthogonal set (meaning that all the columns inside matrix A are orthogonal to each other), then we can find the least-squares solutions using the equation:
Where we have that b^ encompases the orthogonal projection of b onto the columns of A:
Before we continue onto the next section, let us focus for a moment in what is called the least-squares error: Remember in the first section we called the left hand side of equation 1 as the magnitude of the smallest possible error of the best approximation to the vector x, in other words, the magnitude of the smallest possible error in x^. This part of equation one is what is called the least-squares error:
Solving least squares problems
During the next exercises we will take a look at different examples on the method of least squares. Make sure you follow all of the operations and if in doubt, do not hesitate to message us!
Example 1
Given A and b as shown below, find a least squares estimate solution for equation Ax=b.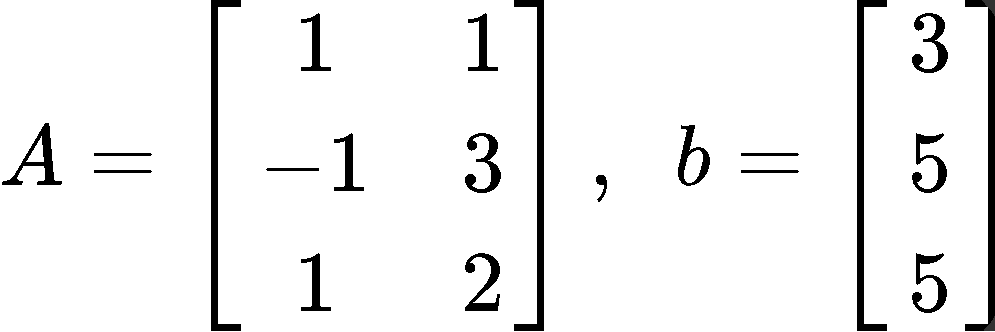
This problem is asking to solve for x^ using the least squares formula as defined in equation 3, and so, we must follow the steps we have described before. The first thing to do is to obtain the transpose of matrix A. Remember that the transpose of a matrix is obtained by swapping the elements that used to form the rows in the original matrix as the columns in the transform, and so, we swap rows to columns and columns to rows to find AT:
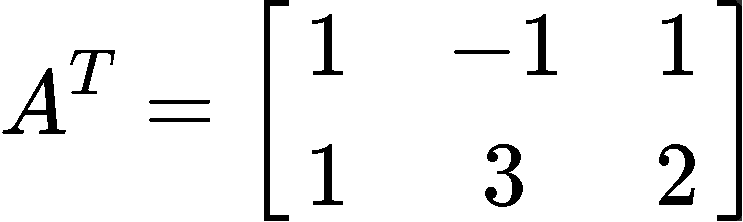
Then we multiply the matrix obtaining through the transpose in equation 8 with matrix A, and so, ATA goes as follows:
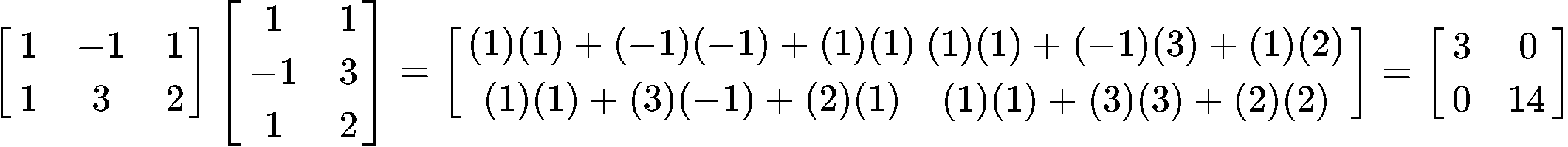
Now we find the inverse of matrix ATA:
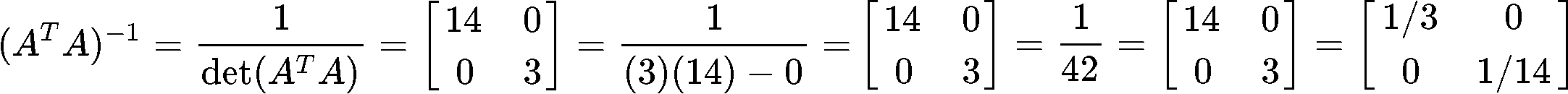
On the other hand, now we multiply the transpose of matrix A, found in equation 8, with the vector b:
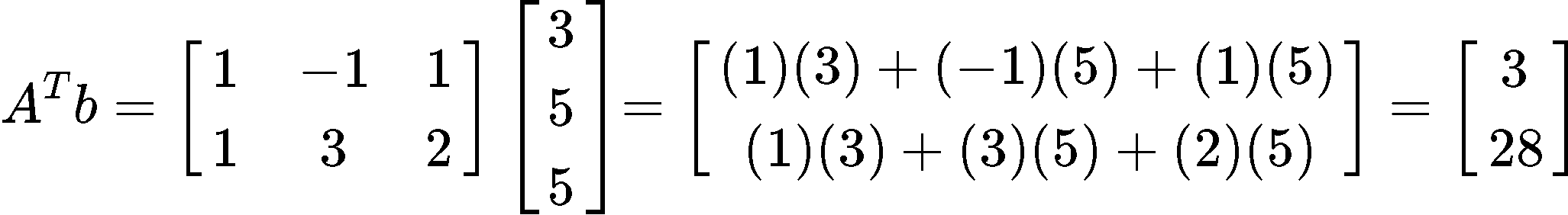
Now we can finally obtain x^ by multiplying the results found in equations 10 and 11: x^=(ATA)−1ATb
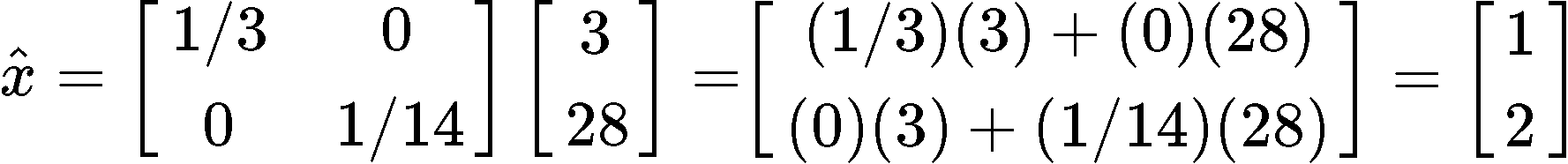
Example 2
Describe all least square solutions of equation Ax=b if: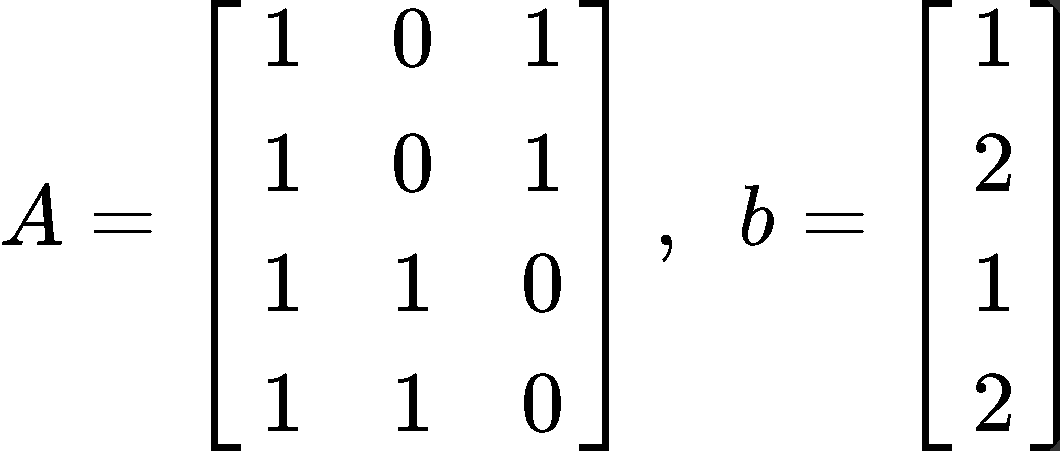
Now following the steps to solve for x^ using the least squares equation 2: ATAx^=ATb
We start by finding the transpose AT:
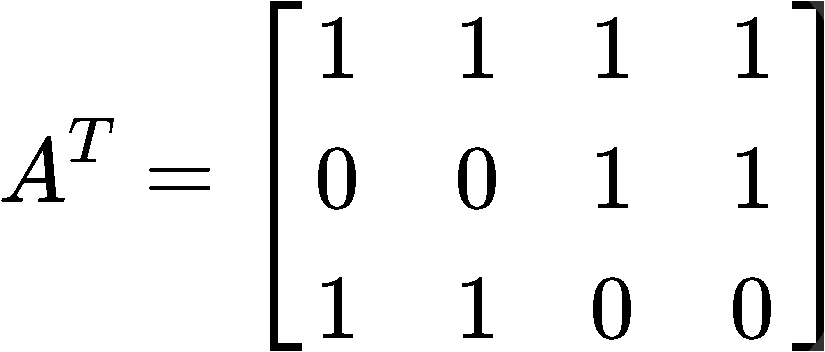
Next, we multiply the transpose to matrix A:
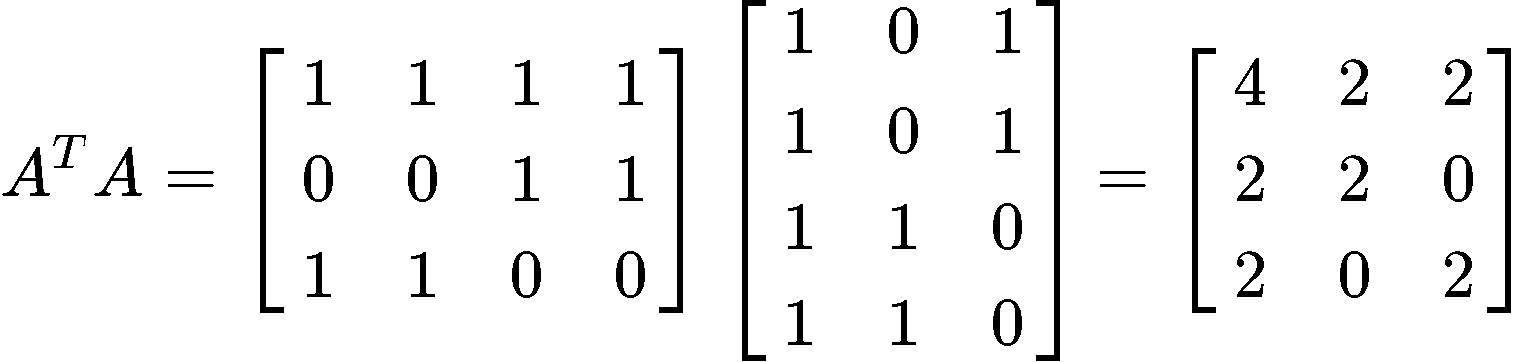
Now we multiply the transpose of matrix A with the vector b:
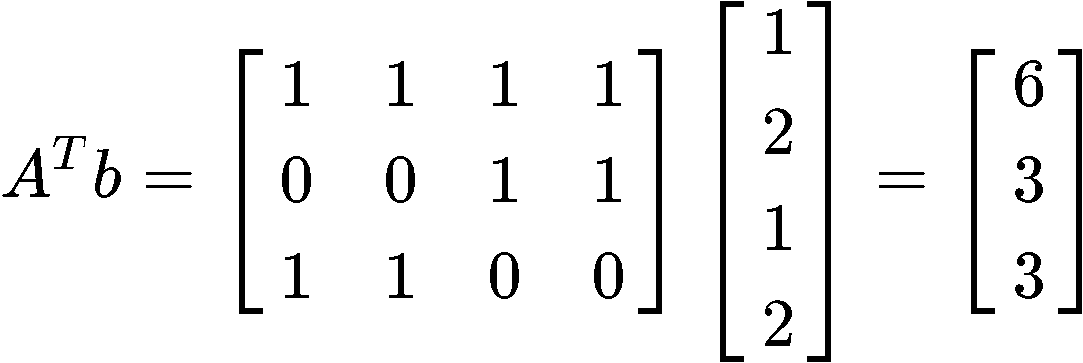
With the results found in equations 15 and 16, we can construct the matrix equation ATAx^=ATb as follows:
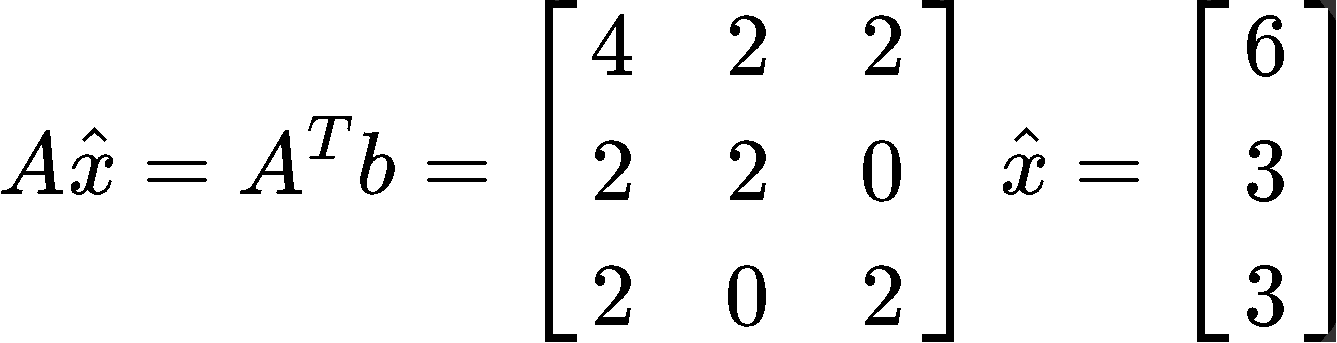
Transform the matrix equation above into an augmented matrix and row reduce it into its echelon form to find the components of vector x^:
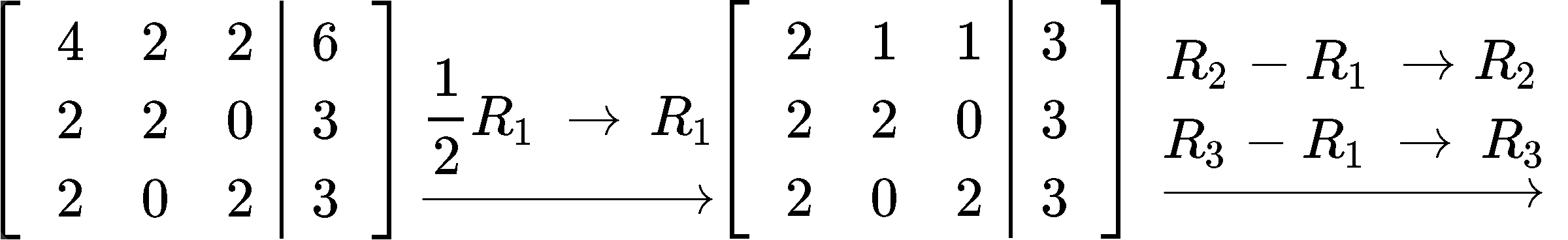
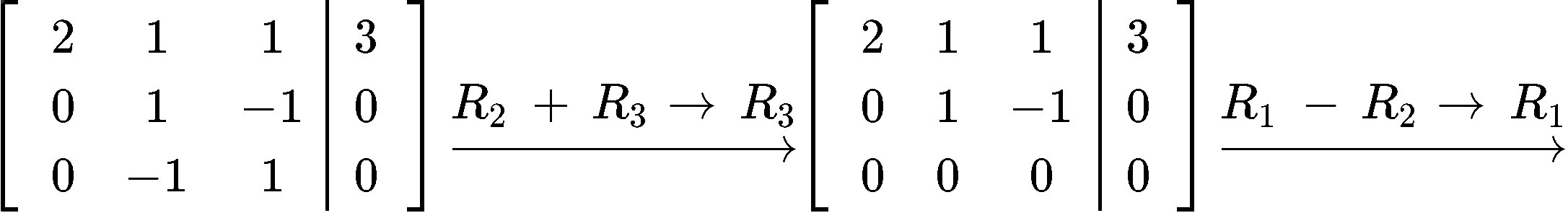
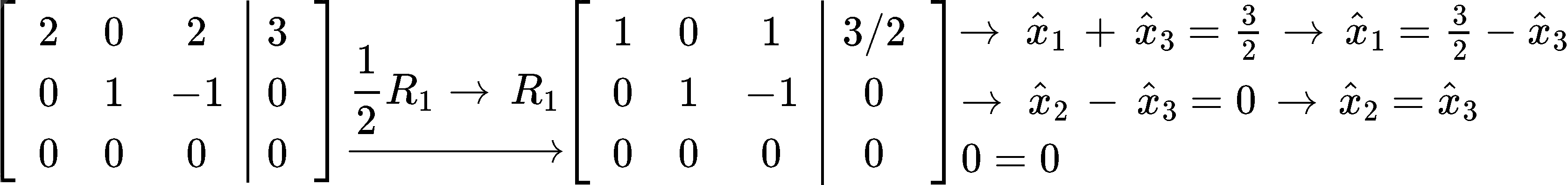
And so, we can construct the least squares solution x^ with the components found:
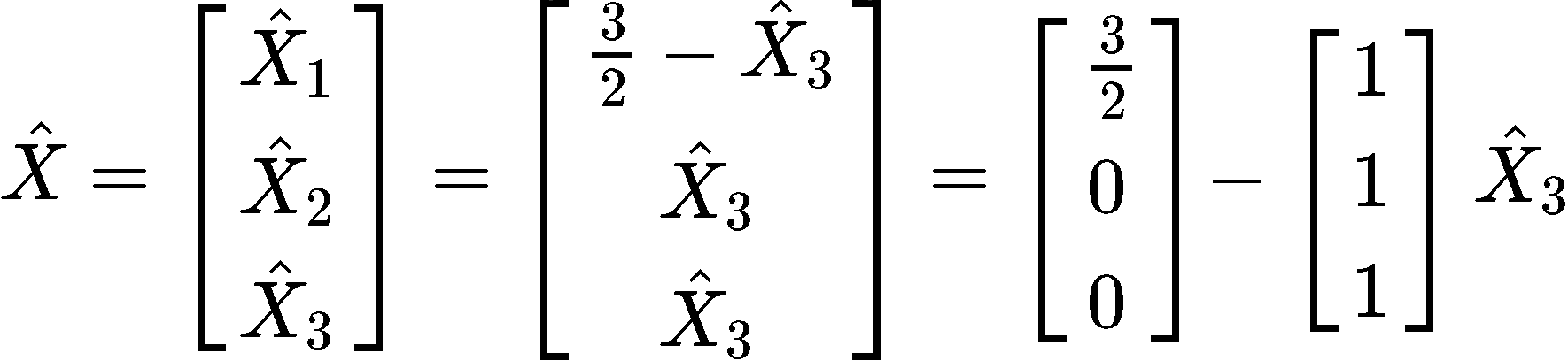
Example 3
You are given that the least squares solution of Ax=b is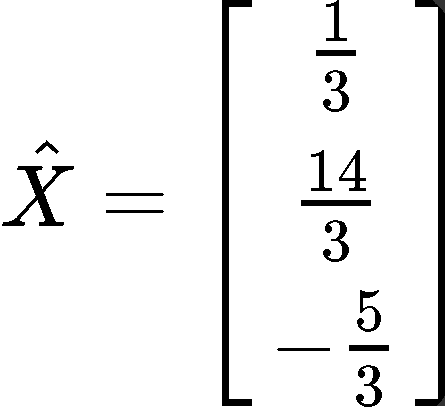
Compute the least square error if A and b are as follows:
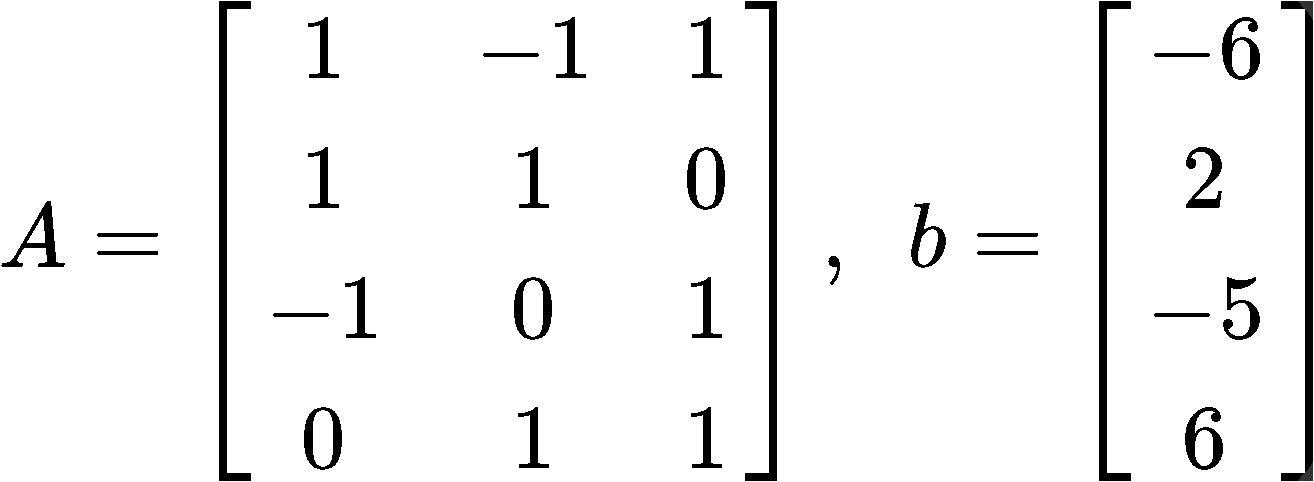
This problem is asking us to calculate the magnitude of the smallest possible error in x^. Such error is defined in equation 6, so now, we just have to follows the next simple steps to compute it:
Start by computing the multiplication Ax^:
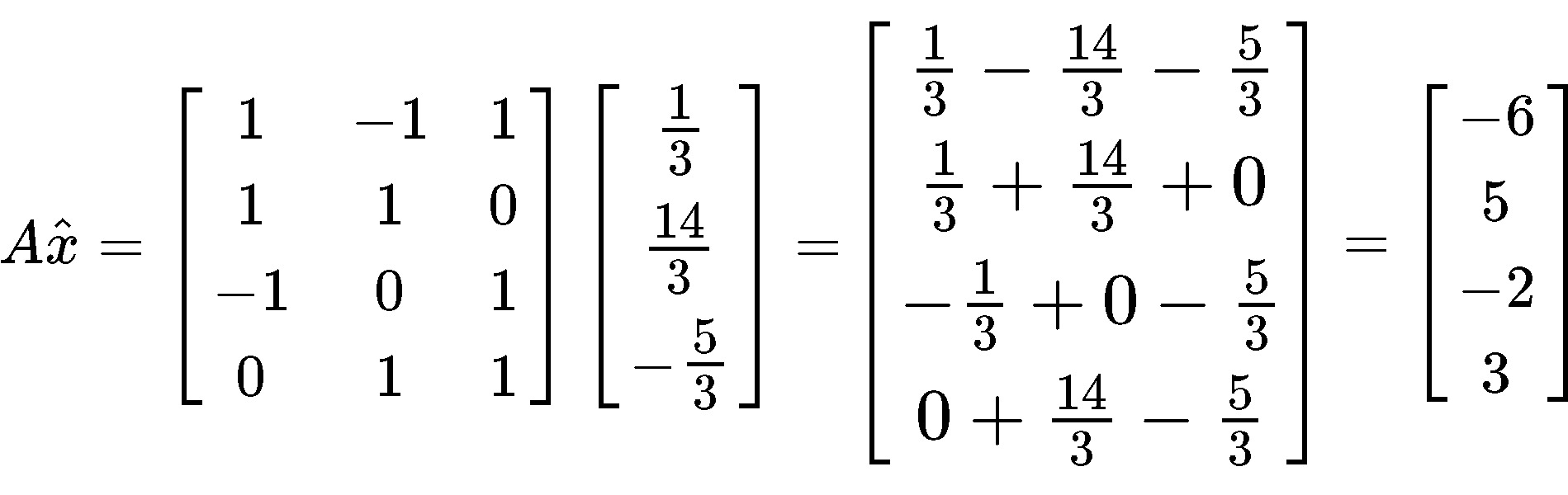
Having found the column vector from the multiplication above, we need to perform a subtraction of vectors by subtracting the vector found in equation 22 to vector b just as shown below:
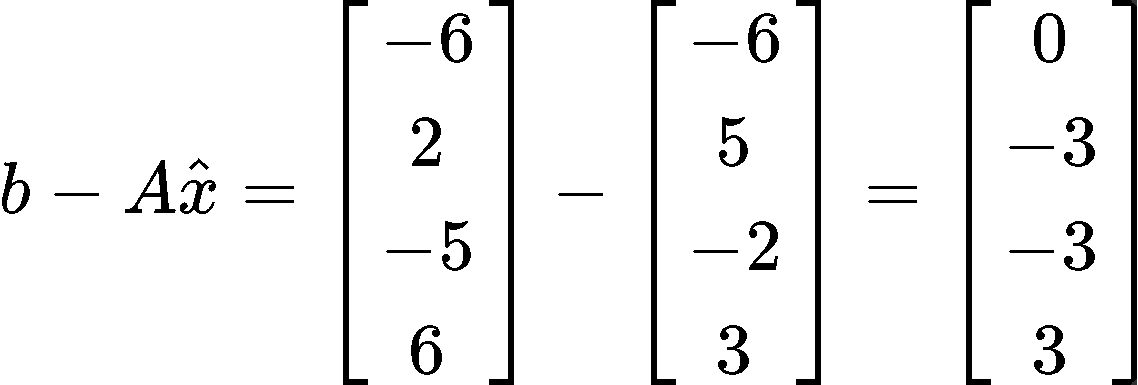
And now, you just need to find the length of the vector found in equation 23. Remember we do that by computing the square root of the addition of the components of the vectors squared:
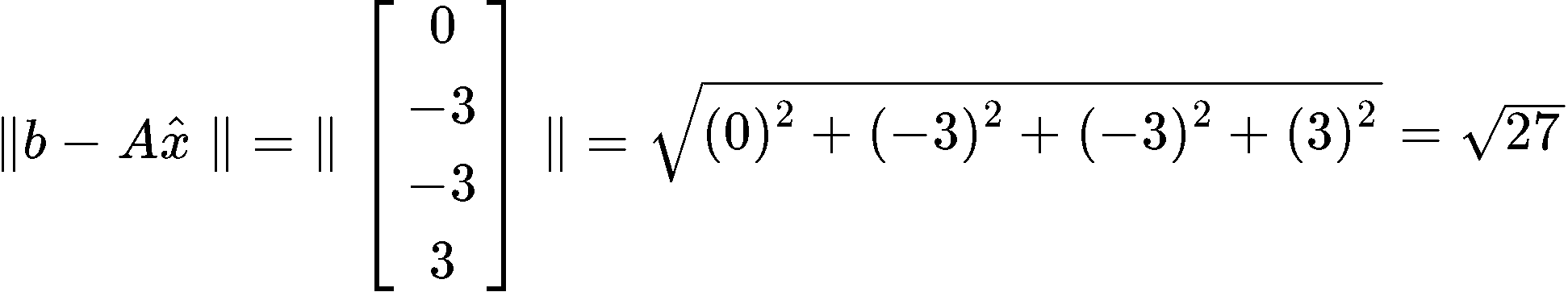
And we are done, the least square error is equal to 27
Example 4
Find the orthogonal projections of b onto the columns of A and find a least-squares solution of Ax=b.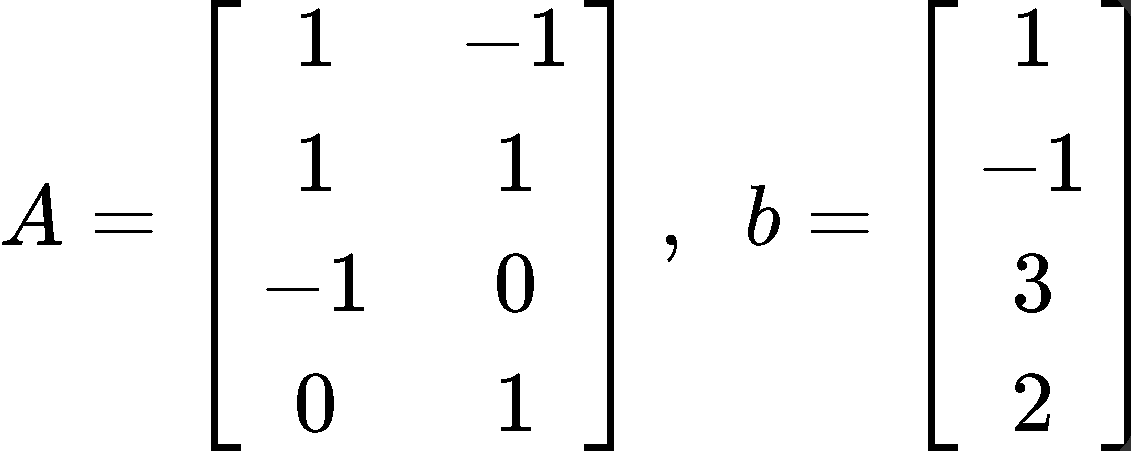
In order to find the orthogonal projections and the least squares solution for this problem we need to use and alternative approach, and so, for this case we start by computing the orthogonal projections of b onto the columns of A using the formula found in equation 5, to the go ahead and solve for the least squares solution using equation 4.
For the orthogonal projections we have that:
Where a1 and a2 are the column vectors that compose the matrix A. Therefore, solving for b^ goes as follows:
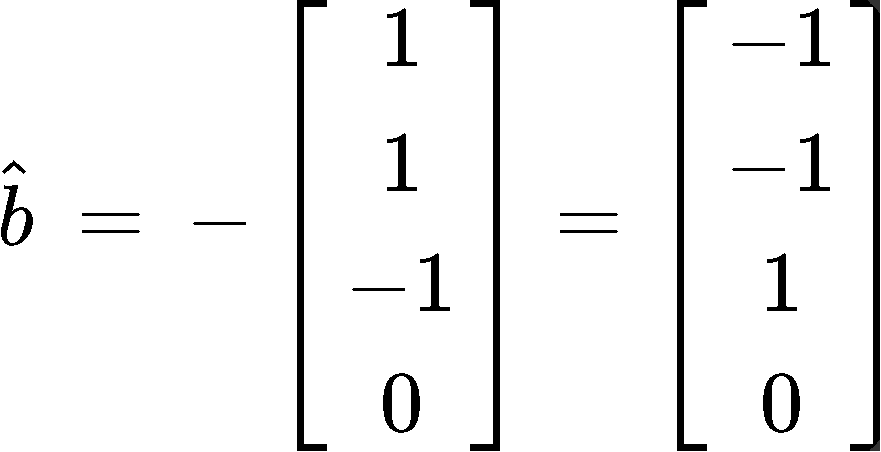
And so, we have found the orthogonal projections. Now for the least squares solution we use as reference equation 4 and take the matrix A and vector b^ so we can form the matrix equation:
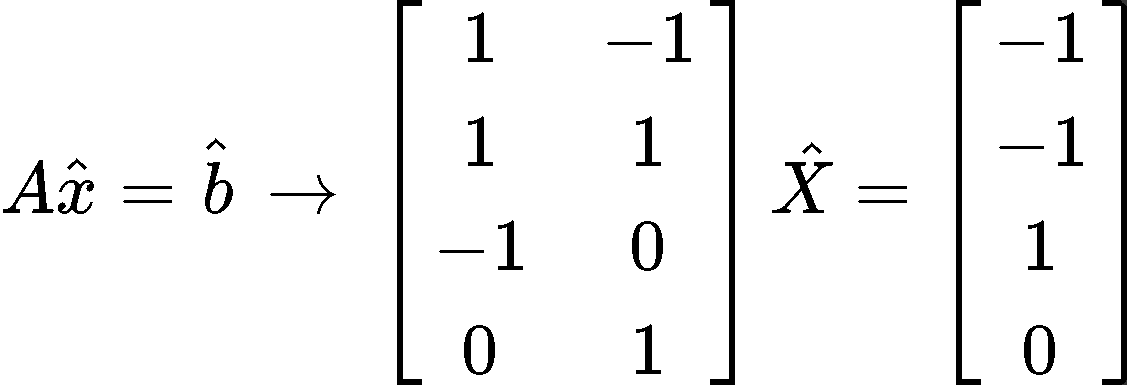
Where we can easily obtain the vector x^ since its components are x1=−1andx2=0, and so:
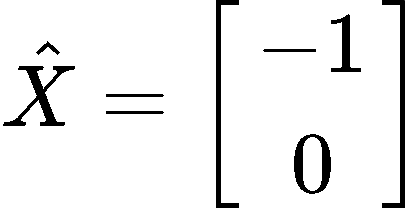
This is it for our lesson on least squares, we hope you enjoyed it, and see you in the next lesson, the final one for this course!
In linear algebra, we have dealt with questions in which Ax=b does not have a solution. When a solution does not exist, the best thing we can do is to approximate x. In this section, we will learn how to find a x such that it makes Ax as close as possible to b.
If A is an m×n matrix and b is a vector in Rn, then a least-squares solution of Ax=b is a x^ in Rn where
∥b−Ax^∥≤∥b−Ax∥
For all x in Rn.
The smaller the distance, the smaller the error. Thus, the better the approximation. So the smallest distance gives the best approximation for x. So we call the best approximation for x to be x^.
The Least-Squares Solution
The set of least-square solutions of Ax=b matches with the non-empty set of solutions of the matrix equation ATAx^=ATb.
In other words,
ATAx^=ATb
→x^=(ATA)−1ATb
Where x is the least square solutions of Ax=b.
Keep in mind that x is not always a unique solution. However, it is unique if one of the conditions hold:
1. The equation Ax=b has unique least-squares solution for each b in Rm.
2. The columns of A are linearly independent.
3. The matrix ATA is invertible.
The Least-Squares Error
To find the least-squares error of the least-squares solution of Ax=b, we compute
∥b−Ax^∥
Alternative Calculations to Least-Squares Solutions
Let A be a m×n matrix where a1,⋯,an are the columns of A. If Col(A)={a1,⋯,an} form an orthogonal set, then we can find the least-squares solutions using the equation
Ax^=b^
where b^=projCol(A)b.
Let A be a m×n matrix with linearly independent columns, and let A=QR be the QR factorization of A. Then for each b in Rm, the equation Ax=b has a unique least-squares solution where
x^=R−1QTb
→Rx^=QTb
If A is an m×n matrix and b is a vector in Rn, then a least-squares solution of Ax=b is a x^ in Rn where
For all x in Rn.
The smaller the distance, the smaller the error. Thus, the better the approximation. So the smallest distance gives the best approximation for x. So we call the best approximation for x to be x^.
The Least-Squares Solution
The set of least-square solutions of Ax=b matches with the non-empty set of solutions of the matrix equation ATAx^=ATb.
In other words,
→x^=(ATA)−1ATb
Where x is the least square solutions of Ax=b.
Keep in mind that x is not always a unique solution. However, it is unique if one of the conditions hold:
1. The equation Ax=b has unique least-squares solution for each b in Rm.
2. The columns of A are linearly independent.
3. The matrix ATA is invertible.
The Least-Squares Error
To find the least-squares error of the least-squares solution of Ax=b, we compute
Alternative Calculations to Least-Squares Solutions
Let A be a m×n matrix where a1,⋯,an are the columns of A. If Col(A)={a1,⋯,an} form an orthogonal set, then we can find the least-squares solutions using the equation
where b^=projCol(A)b.
Let A be a m×n matrix with linearly independent columns, and let A=QR be the QR factorization of A. Then for each b in Rm, the equation Ax=b has a unique least-squares solution where
→Rx^=QTb
2
videos
remaining today
remaining today
5
practice questions
remaining today
remaining today



