Dividing decimals by powers of 10
Topic Notes
In this lesson, we will learn:
- How to move the decimal place when dividing decimals by powers of 10
- How to understand decimal division using base ten (block) models
Notes:
- In the last lesson, we learned that powers of ten represent the repeated multiplication (or repeated division) of the number 10.
- We learned that when multiplying decimals by powers of 10, we look at the power of 10 exponent or the number of zeroes it represents to move decimals places to the right.
- For dividing decimals by powers of 10, we will move the decimal to the left!
- When you divide any number by 1, it stays exactly the same—just like multiplying by 1
- When you divide by 10, 100, and 1000:
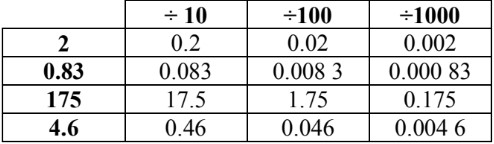
- If there are no more numbers when moving the decimal place to the left, fill those spaces with leading zeroes!
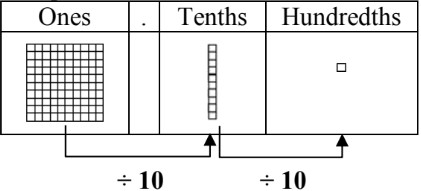
- We can also use base ten (block) models to divide decimals by powers of 10. There are two different models, depending on what represents one whole:
- If one whole is represented by a hundred block (square), each time you divide by 10, you turn your model into the next smaller type: from hundred square → ten stick → one square.
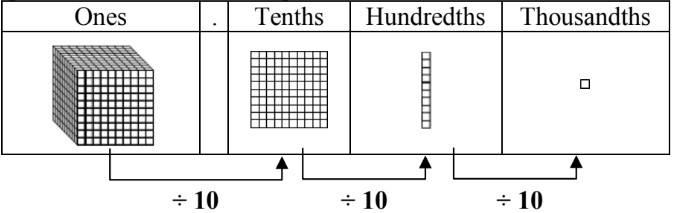
- If whole is represented by a thousand block (cube), each time you divide by 10, you turn your model into the next smaller type: from thousand cube [Symbol] hundred square → ten stick → one square.
Introduction to Dividing Decimals by Powers of 10
Dividing decimals by powers of 10 is a fundamental concept in mathematics that builds upon students' understanding of place value and decimal operations. This video introduces the topic, emphasizing its significance in developing a deeper comprehension of decimal division. A key aspect of this lesson is the use of base 10 block models, which provide a visual representation of the division process. These models help students grasp how the decimal point shifts when dividing by powers of 10, making the abstract concept more concrete and accessible. By utilizing these visual aids, learners can better understand the relationship between the dividend, divisor, and quotient in decimal division. The video demonstrates how dividing by powers of 10 relates to moving digits to the right, effectively decreasing the value of each place. This foundational knowledge is crucial for more advanced mathematical concepts and real-world applications involving decimals and division.
Understanding Base 10 Block Models
Base 10 block models are powerful visual tools that play a crucial role in helping students understand and visualize decimal division and place value concepts. These models consist of different-sized blocks representing various place values in our decimal number system, making abstract mathematical ideas more concrete and accessible.
The base 10 block system typically includes three main types of blocks: hundreds blocks, tens blocks, and ones blocks. Each of these blocks corresponds to a specific place value in our decimal system. The hundreds block is the largest, usually represented by a cube measuring 10x10x10 units. The tens block is a flat rectangle measuring 10x10x1 units, while the ones block is the smallest, typically a small cube measuring 1x1x1 unit.
These blocks are designed to show the relationship between different place values in our decimal system. For instance, it's easy to see that ten ones blocks can be exchanged for one tens block, and ten tens blocks can be exchanged for one hundreds block. This visual representation helps students grasp the concept of regrouping and the hierarchical nature of our number system.
When it comes to decimal place values, base 10 block models extend their usefulness by representing fractional parts of whole numbers. The ones block, which represents a whole unit, can be divided into smaller parts to represent tenths and hundredths. Imagine slicing the ones block into ten equal parts each of these parts would represent one-tenth. Similarly, if we were to divide the ones block into 100 equal parts, each part would represent one-hundredth.
This extension of the base 10 block model to represent decimal fractions is particularly valuable when teaching decimal division. Students can physically manipulate these blocks to understand how whole numbers can be divided into smaller parts and how these parts relate to decimal notation. For example, when dividing 1 by 2, students can see that half of the ones block represents 0.5 or five-tenths.
The importance of base 10 block models in visualizing decimal division cannot be overstated. They provide a tangible way for students to explore and understand the relationships between whole numbers and decimals. By physically manipulating these blocks, students can see how division works, how remainders are handled, and how decimal answers are derived.
Moreover, these models help students develop a strong sense of place value, which is fundamental to understanding our number system. They can easily see how the value of a digit changes depending on its position in a number. This understanding is crucial when working with larger numbers, performing arithmetic operations, and solving more complex mathematical problems.
In conclusion, base 10 block models serve as an invaluable tool in mathematics education, particularly in teaching decimal division and place value concepts. By providing a concrete representation of abstract numerical ideas, these models bridge the gap between conceptual understanding and procedural fluency. They allow students to visualize, explore, and internalize fundamental mathematical principles, laying a solid foundation for more advanced mathematical learning.
Representing Decimals with the Thousand Cube Model
The thousand cube model is a powerful visual tool that helps students understand and represent decimals in a tangible way. This model consists of various blocks that correspond to different place values, making it easier to grasp the concept of decimal notation. By exploring the relationship between the thousand cube, hundreds block, tens block, and ones block, we can gain a deeper understanding of how decimals work and how they relate to whole numbers.
At the heart of the thousand cube model is the thousand cube itself. This large cube represents one whole unit and is typically divided into 1000 smaller cubes. Each of these smaller cubes represents one thousandth (0.001) of the whole. The thousand cube serves as the foundation for understanding how decimals are structured and how they relate to whole numbers.
Moving down in scale, we have the hundreds block. This flat square represents one-tenth (0.1) of the thousand cube. It consists of 100 small cubes arranged in a 10x10 grid. Each small cube in the hundreds block represents one hundredth (0.01) of the whole. This block helps students visualize the concept of tenths and hundredths in decimal notation.
Next, we have the tens block, which is a long rectangular prism made up of 10 small cubes. This block represents one hundredth (0.01) of the whole thousand cube or one-tenth (0.1) of the hundreds block. It helps students understand the relationship between tenths and hundredths in decimal notation.
Finally, we have the ones block, which is a single small cube. This represents one thousandth (0.001) of the whole thousand cube. It is the smallest unit in the model and corresponds to the thousandths place in decimal notation.
The beauty of the thousand cube model lies in its ability to visually represent the relationships between these different place values. Students can easily see that 10 ones blocks make up one tens block, 10 tens blocks make up one hundreds block, and 10 hundreds blocks make up the thousand cube. This hierarchical structure mirrors the base-10 system used in decimal notation.
When working with decimals, students can use these blocks to represent various numbers. For example, 0.234 could be represented by 2 hundreds blocks, 3 tens blocks, and 4 ones blocks. This visual representation helps students understand that 0.234 is made up of 2 tenths, 3 hundredths, and 4 thousandths.
The thousand cube model also helps students understand the concept of place value in decimals. They can see that moving one place to the right (e.g., from tenths to hundredths) makes the value ten times smaller, while moving one place to the left makes it ten times larger. This reinforces the base-10 structure of our number system and helps students develop a strong foundation for working with decimals.
Moreover, the model can be used to demonstrate addition and subtraction of decimals. By physically combining or removing blocks, students can visualize these operations and understand why we need to align decimal points when performing calculations.
In conclusion, the thousand cube model is an invaluable tool for teaching and learning about decimal representation. By providing a concrete, visual representation of abstract concepts, it helps students develop a deep understanding of decimals, place value in decimals, and the relationships between different decimal places. This model bridges the gap between whole numbers and decimals, making it easier for students to grasp these important mathematical concepts and apply them in real-world situations.
Using Block Models to Demonstrate Division by Powers of 10
Block models are powerful visual tools that can help students understand the concept of division by powers of 10. These models provide a concrete representation of how numbers change when divided by 10, 100, or 1000, and they clearly illustrate the relationship between division and decimal point movement. In this section, we'll explore how to use block models effectively to teach this important mathematical concept.
To begin, let's consider the basic structure of block models. Typically, we use two main types: the hundred block and the thousand cube. The hundred block is a flat square divided into 100 smaller squares, representing ones. The thousand cube is a larger cube made up of 1000 smaller cubes, each representing one unit.
When using block models to show division by powers of 10, we focus on the process of dividing blocks into smaller units. This division visually represents how numbers become smaller when divided by 10, 100, or 1000. As we divide the blocks, we can observe how this relates to moving the decimal point in the number being divided.
Let's start with an example of dividing by 10 using the hundred block model:
- Begin with a whole hundred block, representing 100.
- To divide by 10, we need to split the block into 10 equal parts.
- Each part will now represent 10 units (100 ÷ 10 = 10).
- Notice how the decimal point has moved one place to the left: from 100 to 10.0.
This process clearly shows that when we divide by 10, the decimal point moves one place to the left. Students can physically see how the original block is broken down into smaller units, reinforcing the concept of division.
Now, let's look at dividing by 100 using the thousand cube model:
- Start with a thousand cube, representing 1000.
- To divide by 100, we need to split the cube into 100 equal parts.
- Each part will now represent 10 units (1000 ÷ 100 = 10).
- Observe how the decimal point has moved two places to the left: from 1000 to 10.00.
This example demonstrates that when dividing by 100, the decimal point moves two places to the left. The physical act of breaking down the cube into smaller sections helps students visualize the division process and understand why the decimal point moves as it does.
It's important to emphasize the pattern that emerges: for each power of 10 we divide by, the decimal point moves one place to the left. This rule holds true whether we're dividing by 10, 100, 1000, or any other power of 10.
To further reinforce this concept, we can use the block models to show multiple divisions:
- Start with the thousand cube (1000).
- Divide by 10 to get 100 (one hundred block).
- Divide again by 10 to get 10 (one row of the hundred block).
- Divide once more by 10 to get 1 (a single unit cube).
This sequence visually demonstrates how each division by 10 results in a smaller unit and corresponds to moving the decimal point one place to the left: 1000 100.0 10.00 1.000.
Using block models in this way provides students with a tangible, visual representation of division by powers of 10. It helps them understand the abstract concept of decimal point movement by connecting it to the physical act of dividing blocks into smaller units. This approach can be particularly beneficial for visual and kinesthetic learners.
As students become more comfortable with the concept, you can introduce more complex examples, such as dividing decimal numbers by powers of 10.
Relationship Between Place Values and Powers of 10
Understanding the relationship between place values and powers of 10 is fundamental to mastering our decimal number system. This connection forms the backbone of how we represent and manipulate numbers, especially when dealing with large quantities or precise measurements. At its core, our number system is built on the concept of place value, where each digit's position determines its value relative to powers of 10.
In the decimal number system, each place value represents a power of 10. Starting from the ones place and moving left, we encounter increasingly larger powers of 10: ones (10^0), tens (10^1), hundreds (10^2), thousands (10^3), and so on. Conversely, moving to the right of the decimal point, we find decreasing powers of 10: tenths (10^-1), hundredths (10^-2), thousandths (10^-3), etc. This systematic arrangement allows us to represent both very large and very small numbers efficiently.
The beauty of this system lies in how moving from one place value to another involves factors of 10. When we shift a digit one place to the left, we multiply its value by 10. For instance, moving 5 from the ones place to the tens place changes its value from 5 to 50. This is equivalent to multiplying by 10^1 or 10. Similarly, shifting two places to the left multiplies the value by 10^2 or 100. This pattern continues for each leftward shift, multiplying by an additional power of 10.
Conversely, moving a digit to the right divides its value by 10. This is where the concept of decimal point movement comes into play. When we divide a number by 10, the decimal point effectively moves one place to the left. For example, 456 divided by 10 equals 45.6. Notice how each digit has shifted one place to the right relative to the decimal point. This movement represents a division by 10^1 or 10.
Extending this principle, dividing by 100 moves the decimal point two places to the left. For instance, 456 divided by 100 equals 4.56. Each digit has now shifted two places to the right relative to the decimal point, representing a division by 10^2 or 100. This pattern continues for larger divisors that are powers of 10, with the decimal point moving one additional place for each power of 10 in the divisor.
Understanding this relationship is crucial for performing mental math, estimating, and working with scientific notation. It allows us to quickly scale numbers up or down by powers of 10 simply by moving the decimal point. For example, to multiply a number by 1,000, we can move the decimal point three places to the right. To divide by 1,000,000, we move it six places to the left.
This concept also helps in understanding the metric system, where units are related by powers of 10. Moving between units like meters, centimeters, and millimeters involves shifting the decimal point based on the conversion factor, which is always a power of 10.
In conclusion, the relationship between place values and powers of 10 is a powerful tool in mathematics. It simplifies calculations, aids in estimation, and provides a logical structure to our number system. By mastering this concept, we gain a deeper appreciation for the elegance of our decimal system and enhance our ability to work with numbers across a wide range of magnitudes.
Practice Problems and Applications
To help students solidify their understanding of dividing decimals by powers of 10, let's explore a set of practice problems using both hundred block and thousand cube models. These exercises will reinforce the concepts and provide step-by-step solutions for each problem.
Problem 1: Hundred Block Model
Divide 4.5 by 10 using the hundred block model.
Solution:
- Represent 4.5 on the hundred block model.
- Divide by 10 by moving the decimal point one place to the left.
- The result is 0.45.
Explanation: When dividing by 10, each digit moves one place to the right on the place value chart, effectively shifting the decimal point one place to the left.
Problem 2: Thousand Cube Model
Divide 23.7 by 100 using the thousand cube model.
Solution:
- Represent 23.7 on the thousand cube model.
- Divide by 100 by moving the decimal point two places to the left.
- The result is 0.237.
Explanation: Dividing by 100 shifts each digit two places to the right on the place value chart, moving the decimal point two places to the left.
Problem 3: Hundred Block Model
Divide 0.8 by 10 using the hundred block model.
Solution:
- Represent 0.8 on the hundred block model.
- Divide by 10 by moving the decimal point one place to the left.
- The result is 0.08.
Explanation: When dividing a decimal less than 1 by 10, we still move the decimal point one place to the left, adding a zero if necessary.
Problem 4: Thousand Cube Model
Divide 156.3 by 1000 using the thousand cube model.
Solution:
- Represent 156.3 on the thousand cube model.
- Divide by 1000 by moving the decimal point three places to the left.
- The result is 0.1563.
Explanation: Dividing by 1000 shifts each digit three places to the right on the place value chart, moving the decimal point three places to the left.
Problem 5: Mixed Model
Divide 7.25 by 10 using either the hundred block or thousand cube model.
Solution:
- Represent 7.25 on the chosen model.
- Divide by 10 by moving the decimal point one place to the left.
- The result is 0.725.
Explanation: Regardless of the model used, dividing by 10 always shifts the decimal point one place to the left.
Problem 6: Application
A recipe calls for 3.5 cups of flour. If you want to make one-tenth of the recipe, how much flour do you need?
Solution:
- Divide 3.5 by 10.
- The result is 0.35 cups of flour.
Explanation: When dividing decimals by powers of 10, the decimal point moves to the left by the number of zeros in the power of 10.
Conclusion and Key Takeaways
In this article, we explored the essential concept of understanding decimal division by powers of 10 using block models. We learned how to visualize and understand the process of dividing decimals by 1000, 100, and 1000. Block models serve as powerful tools to represent decimal values and their divisions, making abstract mathematical concepts more tangible for students. The importance of using these visual aids cannot be overstated, as they significantly enhance comprehension and problem-solving skills. We encourage you to practice with the provided examples and seek additional resources to reinforce your understanding. Remember, the introductory video offers valuable insights into this concept, so revisiting it can be beneficial. By mastering dividing decimals by 1000, you'll build a strong foundation for more advanced mathematical concepts. Keep practicing, stay curious, and don't hesitate to ask questions as you continue your journey in mathematics.
Introduction to Dividing Decimals by Powers of 10
How can we use base ten (block) models to show decimal division with powers of 10?
Step 1: Understanding the Base Ten Block Models
To begin with, it's essential to understand the base ten block models. These models consist of different blocks representing different place values. The primary blocks include the hundred block, the ten block, and the one block. The hundred block is a large square made up of 100 smaller squares, the ten block is a column of 10 smaller squares, and the one block is a single small square. These blocks help visualize the concept of place value in a tangible way.
Step 2: Establishing the Frame of Reference
Before using the base ten blocks for division, we need to establish our frame of reference. This means determining what each block represents in terms of place value. For instance, if we decide that one whole is represented by the hundred block, then the ten block represents one-tenth, and the one block represents one-hundredth. This setup helps us understand how to break down and divide the blocks when working with decimals.
Step 3: Using the Hundred Block Model
In the hundred block model, one whole is represented by the hundred block. This block is divided into 100 smaller squares, each representing one-hundredth. When dividing by powers of 10, we can visualize the process by breaking down the hundred block into smaller units. For example, dividing the hundred block by 10 means splitting it into ten equal parts, each part being a ten block. This helps us see that dividing by 10 moves us one place value to the right, from the ones place to the tenths place.
Step 4: Using the Thousand Cube Model
Another model we can use is the thousand cube model. In this model, one whole is represented by a large 3D cube made up of 1,000 smaller cubes. Each smaller cube represents one-thousandth. When dividing by powers of 10, we can break down the thousand cube into smaller units. For instance, dividing the thousand cube by 10 means splitting it into ten equal parts, each part being a hundred block. This visualization helps us understand that dividing by 10 moves us one place value to the right, from the ones place to the tenths place, and so on.
Step 5: Visualizing Division with Powers of 10
To visualize division with powers of 10 using base ten blocks, we need to understand the relationship between the blocks and place values. When we divide by 10, we move one place value to the right. For example, if we have a hundred block and divide it by 10, we get ten ten blocks. Each ten block represents one-tenth of the original hundred block. Similarly, if we divide a ten block by 10, we get ten one blocks, each representing one-hundredth of the original hundred block.
Step 6: Applying the Concept to Decimal Division
Now that we understand how to use base ten blocks to visualize division by powers of 10, we can apply this concept to decimal division. For example, if we want to divide 0.5 by 10, we can use the base ten blocks to represent 0.5 as five ten blocks. Dividing these five ten blocks by 10 means splitting each ten block into ten one blocks, resulting in 0.05. This process helps us see that dividing by 10 moves the decimal point one place to the left.
Step 7: Practice and Reinforcement
To reinforce the concept of dividing decimals by powers of 10 using base ten blocks, it's essential to practice with different examples. By working through various problems and visualizing the division process with the blocks, students can develop a deeper understanding of how place value and division by powers of 10 are interconnected. This hands-on approach makes the abstract concept of decimal division more concrete and accessible.
FAQs
Here are some frequently asked questions about dividing decimals by powers of 10:
1. What happens to the decimal point when dividing by powers of 10?
When dividing a decimal by a power of 10, the decimal point moves to the left. The number of places it moves corresponds to the number of zeros in the power of 10. For example, when dividing by 10 (one zero), the decimal point moves one place left; when dividing by 100 (two zeros), it moves two places left; and when dividing by 1000 (three zeros), it moves three places left.
2. How do base 10 block models help in understanding decimal division?
Base 10 block models provide a visual representation of decimal division. They help students see how the value of each digit changes when divided by powers of 10. These models make it easier to understand the concept of place value and how it relates to division by powers of 10, making abstract mathematical ideas more concrete and accessible.
3. Can you divide a number smaller than 1 by a power of 10?
Yes, you can divide a number smaller than 1 by a power of 10. The same rule applies: move the decimal point to the left by the number of zeros in the power of 10. For example, 0.5 ÷ 10 = 0.05. If necessary, add zeros to the left of the decimal point to represent the result correctly.
4. How does dividing by powers of 10 relate to the metric system?
The metric system is based on powers of 10, making conversions between units straightforward. When converting to a smaller unit (e.g., meters to centimeters), you multiply by a power of 10, moving the decimal point right. When converting to a larger unit (e.g., millimeters to meters), you divide by a power of 10, moving the decimal point left. This direct relationship makes metric conversions much simpler than other measurement systems.
5. Why is it important to understand division by powers of 10?
Understanding division by powers of 10 is crucial for several reasons. It forms the foundation for working with decimals, percentages, and scientific notation. This knowledge is essential for performing mental math, estimating large numbers, and solving real-world problems involving measurements and calculations. It also prepares students for more advanced mathematical concepts and is widely applicable in fields such as science, engineering, and finance.
Prerequisite Topics for Dividing Decimals by Power of 10
Understanding the concept of dividing decimals by powers of 10 is crucial in mathematics, but it's essential to grasp certain foundational topics first. One of the most important prerequisites is place value. This concept forms the backbone of our number system and is vital when working with decimals and powers of 10.
When we divide a decimal by a power of 10, we're essentially shifting the decimal point. This operation directly relates to place value, as each shift represents a change in the value of each digit. For instance, when dividing by 10, each digit moves one place to the right, effectively decreasing its value tenfold. This understanding of how digits' positions affect their values is fundamental to mastering division by powers of 10.
Another crucial prerequisite is a solid grasp of dividing decimals. While dividing by powers of 10 is a specific case, it builds upon the general principles of decimal division. Understanding how to perform basic decimal divisions, including dividing decimals by 1000 and other powers of 10, provides a strong foundation for more complex operations.
Moreover, recognizing the relationship between two variables is also relevant to this topic. In the context of dividing decimals by powers of 10, it's important to understand the relationship between dividend, divisor, and quotient. As the power of 10 (the divisor) increases, the quotient decreases proportionally. This inverse relationship is a key concept in understanding how division by powers of 10 affects the magnitude of numbers.
By mastering these prerequisite topics, students can approach dividing decimals by powers of 10 with confidence. Place value provides the conceptual framework, understanding decimal division offers practical skills, and recognizing relationships between variables helps in predicting and verifying results. Together, these foundational concepts create a robust platform for tackling more advanced mathematical operations involving decimals and powers of 10.
In conclusion, the journey to proficiency in dividing decimals by powers of 10 is built upon these interconnected concepts. Each prerequisite topic contributes uniquely to the overall understanding, forming a comprehensive knowledge base. As students progress, they'll find that these fundamental principles continue to apply and evolve, supporting their mathematical growth across various topics and complexity levels.

