Counting forwards
Topic Notes
In this lesson, we will learn:
- How do we count forwards using: the numbers 0 to 9, number lines (and negative numbers), and big numbers (up to millions)?
- Counting forwards can help us write addition statements.
Notes:
- We use numbers to represent how many things there are.
- You can count how many things there are by counting FORWARDS:
- 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …
- Technically, the number line starts at 0 but zero means there are no things to count. That’s why you start counting at 1
- Counting forwards means the counting numbers are getting BIGGER
- If you look at a number line, counting forwards means going from left to right

- Negative numbers also count forward by going from left to right on a number line
- Don’t get confused! The negative numbers (digits) are going backwards, but they have a negative sign!
- The smaller your negative, the bigger your value (less negative = bigger)
- Ex. counting forwards in negatives: -5, -4, -3, -2, -1, 0
- Recall: number PLACE VALUES!
- The smaller place values are on the right, the bigger place values are on the left
- When the digit increases (from 0 to 9): after you hit 9, next you will increase 1 into the place value on the left. Your digit will then start again from 0 (and count up to 9, repeating the process)
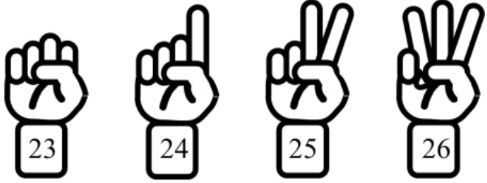
- You can also use your fingers to count forward and find out how many numbers you have increased (counted up) by.
- Put down all your fingers (zero fingers up) when you start on your first number.
- Each number you count, raise one more finger.
- When you reach your last number, you can count your raised fingers
- Ex. counting from 23 up to 26: you count up by three
- This can allow you to make addition statements!
- [starting #] + [how much you counted up] = [last #]
- Ex. counting from 23 up to 26, the addition statement would be: 23 + 3 = 26

Introduction to Counting Forwards
Counting forwards is a fundamental mathematical skill that forms the basis for more advanced numerical concepts. Our introduction video serves as an essential starting point, providing a clear and engaging overview of this crucial topic. By watching this video, learners will gain a solid understanding of the number sequence and how to progress through it. In this article, we'll delve deeper into the various aspects of counting forwards, including practical methods for counting objects, utilizing number lines as visual aids, and extending our counting skills to larger numbers. These techniques will help reinforce the concept of numerical order and build confidence in working with numbers. Whether you're a beginner or looking to refresh your skills, mastering the art of counting forwards is an invaluable step in your mathematical journey. Join us as we explore this foundational concept and unlock the door to more advanced mathematical thinking.
Counting Objects and Basic Number Sequence
Counting objects is a fundamental skill that we learn early in life, and it forms the basis of our understanding of mathematics. Let's explore this concept using a fun and relatable example: counting objects like dogs at a dog park. Imagine you're at a bustling dog park on a sunny afternoon. As you watch the playful pups run around, you decide to count them.
When we start counting objects, we always begin with the number one. This is because counting is about determining the quantity of things present, and we start with the first item we see. So, as you spot the first dog, you say "one." Then, as you notice the next dog, you say "two," and so on. This process continues as you count each dog in the park, following the natural number sequence: one, two, three, four, five, and upwards.
The number sequence we use for counting is based on digits from 0 to 9. These digits are the building blocks of our number system. When counting objects, we use combinations of these digits to represent quantities. For example, when you count 12 dogs, you're using the digits 1 and 2 together. As the count gets higher, you'll use more digits: 25 dogs would use 2 and 5, 108 dogs would use 1, 0, and 8, and so on.
It's important to note that while zero is a crucial digit in our number system, we don't typically use it when counting objects. Zero represents the absence of quantity, so it doesn't make sense to start counting with zero when objects are present. In our dog park example, you wouldn't say "zero" before counting the first dog because that would imply there are no dogs to count.
However, zero plays a vital role in our number system. It allows us to represent larger numbers and perform calculations. For instance, if you wanted to write down that you counted 100 dogs, you'd use the digit zero twice. Without zero, we couldn't easily represent numbers like 10, 20, 30, and so on.
As you continue counting dogs in the park, you'll notice that the number sequence follows a predictable pattern. After nine, we move to double digits starting with 10, then 11, 12, and so forth. This pattern repeats with each new tens place: 20, 21, 22... 30, 31, 32... and continues infinitely. Understanding this pattern is crucial for developing number sense and advancing mathematical skills.
Counting objects also helps us understand the concept of "how many." Each number in the counting sequence represents a specific quantity. So if you count 15 dogs, you know there are exactly that many dogs in the park no more, no less. This one-to-one correspondence between numbers and objects is a fundamental principle in mathematics.
As children learn to count, they often start by reciting numbers in order without fully grasping the quantity each number represents. With practice and experience, like counting dogs in a park, they begin to understand that each number corresponds to a specific amount. This understanding is crucial for developing more advanced mathematical concepts like addition, subtraction, and beyond.
In conclusion, counting objects, like dogs in a park, is an essential skill that introduces us to the number sequence and helps us understand quantity. Starting with one and progressing through the digits 0 to 9, we can represent any number of objects. While zero isn't used in the actual counting process, it's a vital digit in our number system. By mastering counting, we lay the foundation for a lifetime of mathematical understanding and problem-solving skills.
Number Lines and Counting Forwards
Number lines are fundamental tools in mathematics that visually represent the sequence of numbers. They play a crucial role in helping us understand the concept of counting forwards and the relationships between different numbers. A number line is essentially a straight line with evenly spaced points, each representing a number. This visual representation makes it easier to grasp the idea of increasing values and the direction of counting.
When we talk about counting forwards on a number line, we're referring to the process of moving to the right. This rightward movement corresponds to increasing values, which is the essence of counting forwards. As we progress along the number line from left to right, each step represents an increase by one. This concept is particularly helpful for young learners who are just beginning to understand the sequence of numbers and how they relate to each other.
The beauty of a number line lies in its simplicity and versatility. It starts with zero at the center, and positive numbers extend to the right. Each mark to the right of zero represents a whole number that's one more than the previous one. This visual representation reinforces the idea that counting forwards means moving to higher numbers, making it an invaluable tool for teaching basic arithmetic concepts.
But what happens when we move to the left of zero on a number line? This is where the concept of negative numbers comes into play. Negative numbers are an essential part of mathematics, representing values less than zero. On a number line, these numbers are positioned to the left of zero, extending infinitely in that direction. Understanding negative numbers is crucial for developing a comprehensive grasp of the number system and advanced mathematical concepts.
Interestingly, the concept of counting forwards applies to negative numbers as well, albeit in a slightly different way. When we count forwards starting from a negative number, we're still moving to the right on the number line. For example, if we start at -5 and count forwards, we move through -4, -3, -2, -1, and eventually reach 0 before continuing into positive numbers. This demonstrates that counting forwards always involves moving to the right on a number line, regardless of whether we're dealing with positive or negative numbers.
The relationship between negative numbers and counting forwards on a number line helps students understand the concept of absolute value. As we count forwards from negative numbers towards zero, the absolute value decreases, even though we're moving towards higher numbers. This seemingly counterintuitive idea becomes clear when visualized on a number line, highlighting the importance of this tool in mathematical education.
Number lines also serve as a bridge to more advanced mathematical concepts. They provide a foundation for understanding fractions, decimals, and even complex numbers. By extending the number line to include these more sophisticated number types, students can build upon their basic understanding of counting forwards and apply it to more complex mathematical operations.
In conclusion, number lines are invaluable tools for visualizing the concept of counting forwards and understanding the relationships between numbers. They provide a clear representation of increasing values as we move to the right and help explain the role of negative numbers in our number system. By mastering the use of number lines, students develop a strong foundation for more advanced mathematical concepts, making them an essential component of mathematical education.
Place Values and Counting Large Numbers
Understanding place values is crucial when it comes to counting large numbers. Place values refer to the position of each digit in a number and determine its value. In our decimal system, we have ones, tens, hundreds, thousands, and so on. Each place value is ten times greater than the one to its right.
Let's start with the basics. In the number 123, we have:
- 3 in the ones place
- 2 in the tens place
- 1 in the hundreds place
This means 123 is actually 100 + 20 + 3. Understanding this concept is essential for counting large numbers accurately.
Now, let's explore how to count from 1 to 1000. We begin with single digits from 1 to 9, which occupy the ones place. When we reach 10, we introduce the tens place. We continue counting from 10 to 99, increasing the tens digit each time we complete a set of ten.
The transition from 99 to 100 is significant as it introduces the hundreds place. At this point, we have:
- 0 in the ones place
- 0 in the tens place
- 1 in the hundreds place
We then continue the pattern, counting from 100 to 999. During this process, we cycle through the ones and tens digits while keeping the hundreds digit constant until we complete each hundred.
The transition from 999 to 1000 is another crucial point. Here's what happens:
- 999: 9 hundreds, 9 tens, 9 ones
- 1000: 1 thousand, 0 hundreds, 0 tens, 0 ones
This introduces the thousands place, marking our entry into four-digit numbers.
To illustrate these concepts further, let's look at some examples:
- 245: 2 hundreds, 4 tens, 5 ones (200 + 40 + 5)
- 507: 5 hundreds, 0 tens, 7 ones (500 + 0 + 7)
- 1,234: 1 thousand, 2 hundreds, 3 tens, 4 ones (1000 + 200 + 30 + 4)
When dealing with larger numbers, we continue to add new place values. After thousands, we have ten thousands, hundred thousands, millions, and so on. Each new place value is created when we multiply the previous one by ten.
Understanding place values helps us read and write large numbers correctly. For instance, 5,280,371 can be broken down as:
- 5 millions
- 2 hundred thousands
- 8 ten thousands
- 0 thousands
- 3 hundreds
- 7 tens
- 1 one
This system allows us to represent enormous quantities with just ten digits (0-9) by utilizing place values.
In conclusion, mastering place values and understanding how they work in counting large numbers is fundamental to mathematical literacy. It enables us to comprehend, manipulate, and work with numbers of any size, from basic counting to complex calculations in various fields like science, engineering, and finance.
Counting Forwards and Addition
Counting forwards is a fundamental skill that directly relates to addition, forming the basis for early mathematical understanding. When children learn to count forwards, they are essentially performing a series of additions by one. This connection between counting and addition is crucial for developing number sense and arithmetic skills.
The relationship between counting forwards and addition becomes clear when we consider that adding is simply a more efficient way of counting. For instance, when we add 3 + 4, we can think of it as counting forward 4 steps from 3. This mental process of moving forward along the number line is at the heart of addition.
There are several methods for counting the difference between numbers, which can be used to solve simple addition problems. These methods include using fingers, counting jumps, and underlining. Let's explore each of these techniques:
1. Using Fingers: This tactile method is often the first strategy children use. To add 5 + 3, a child might hold up 5 fingers on one hand, then count on 3 more fingers on the other hand. By counting all the fingers, they arrive at the sum of 8. This method is particularly useful for small numbers and helps reinforce the concept of counting forwards.
2. Counting Jumps: This method involves visualizing or drawing number jumps on a number line. For example, to solve 7 + 4, start at 7 and make 4 jumps forward: 8, 9, 10, 11. The final landing point is the sum. This technique helps children understand addition as movement along a number sequence and reinforces the connection between counting forwards and adding.
3. Underlining: This written method is useful for slightly larger numbers. To add 12 + 5, write the numbers from 12 to 20 in a line. Then, starting from 12, underline 5 numbers. The last underlined number is the sum. This method visually represents the process of counting forwards and helps children see addition as an extension of the counting sequence.
These methods can be applied to solve various simple addition problems. For instance, when adding 6 + 5:
- Using fingers: Hold up 6 fingers, then count on 5 more, reaching a total of 11.
- Counting jumps: Start at 6 and make 5 jumps forward (7, 8, 9, 10, 11).
- Underlining: Write numbers 6 to 15, then underline 5 numbers starting from 6. The last underlined number is 11.
As children become more proficient, they can use these methods as stepping stones to more advanced mental math strategies. For example, they might learn to start with the larger number and count on, recognizing that 6 + 5 is the same as starting at 6 and counting forward 5 more.
Understanding the relationship between counting forwards and addition helps build a strong foundation for more complex mathematical concepts. It allows children to see numbers as part of a continuous sequence and addition as a way to move along that sequence. This connection also supports the development of mental math skills and number fluency.
By practicing these counting methods, children not only improve their addition skills but also enhance their overall number sense. They begin to recognize patterns in the number system and develop strategies for manipulating numbers mentally. This foundational understanding is crucial for future mathematical learning, including subtraction, multiplication, and division.
In conclusion, the link between counting forwards and addition is a key concept in early mathematics education. By utilizing methods such as finger counting, number jumps, and underlining, children can effectively bridge the gap between simple counting and more complex addition problems. These strategies provide concrete ways to visualize and solve addition problems, reinforcing the fundamental connection between counting and adding.
Practical Applications of Counting Forwards
Counting forwards is a fundamental skill that children use in various real-life situations. This essential math concept has numerous practical applications that make it crucial for young learners to master. From keeping score in games to handling money and measuring time, counting forwards plays a vital role in everyday activities.
One common application of counting forwards is in sports and games. Children often need to keep track of scores, whether it's counting points in a board game or tallying goals in a soccer match. This practical use of counting not only reinforces the skill but also makes it fun and engaging for kids.
Handling money is another important area where counting forwards comes into play. As children learn to count coins and bills, they develop a better understanding of currency and basic financial concepts. This skill becomes particularly useful when making small purchases or saving up for a desired item.
Measuring time is yet another practical application of counting forwards. Children learn to count minutes and hours, which helps them understand the passage of time and develop time management skills. This ability is crucial for following schedules, estimating durations, and planning activities.
Parents and educators can encourage children to practice counting forwards in everyday situations. For instance, counting steps while walking, keeping track of items while grocery shopping, or counting objects around the house are simple yet effective ways to reinforce this skill.
Age-appropriate activities and games can make counting practice more enjoyable for children. Here are some ideas:
- Hopscotch: Draw a hopscotch grid and have children count aloud as they hop through the squares.
- Counting jar: Fill a jar with small objects and ask children to count them, making it a fun estimation game.
- Number line jumps: Create a number line on the floor and have kids jump forward, counting as they go.
- Dice games: Use dice to practice addition while counting forwards.
- Counting songs: Incorporate catchy tunes that involve counting to make learning more memorable.
By integrating counting forwards into everyday activities and games, children can develop a strong foundation in this essential math skill. These practical applications not only reinforce learning but also demonstrate the relevance of counting in real-life situations, making math more accessible and enjoyable for young learners.
Conclusion
In this article, we've explored the fundamental concept of counting forwards, a crucial skill in early math development. The introduction video provided a clear visual demonstration of this concept, making it easier for learners to grasp. We've covered the basics of starting from any number and progressing in a sequential order, emphasizing the importance of understanding number relationships. Practice is key to mastering counting forwards, so we encourage you to incorporate this skill into daily activities, such as counting steps, objects, or even during playtime. Remember, counting forwards is the foundation for more advanced math skills, including addition and skip counting. To further enhance your math learning journey, explore our additional resources and interactive exercises. Don't hesitate to revisit the introduction video for reinforcement. By consistently practicing counting forwards in various situations, you'll build a strong mathematical foundation for future success. Keep counting and happy learning!
Introduction to Counting Forwards: How do we count forwards?
Counting forwards is a fundamental skill that helps us understand numbers and their order. In this guide, we will explore the concept of counting forwards step by step, ensuring a clear and comprehensive understanding of the process.
Step 1: Understanding Counting
Before diving into counting forwards, it's essential to understand what counting is. Counting involves assigning numbers to different objects to determine how many of those objects are present. For example, if you go to a dog park and want to count the number of dogs, you are engaging in the process of counting.
Step 2: Assigning Numbers to Objects
When counting, each object is assigned a unique number. This helps in keeping track of the total number of objects. For instance, if you see four dogs at the park, you would assign the numbers one, two, three, and four to each dog respectively. This way, you can easily determine that there are four dogs in total.
Step 3: Starting with One
Counting forwards always begins with the number one. This is because zero represents the absence of any objects. If there were no dogs at the park, you would say there are zero dogs. However, as soon as you see an object to count, you start with one. So, the first dog you see is counted as one.
Step 4: Counting Each Object Once
Each object should be counted only once to avoid any confusion. For example, if you see four dogs, you count each dog once: one, two, three, and four. This ensures that you have an accurate count of the total number of objects.
Step 5: Using Digits from Zero to Nine
When counting forwards, we use the digits from zero to nine. These digits form the basis of our number system. However, as mentioned earlier, we usually start counting from one. The digits zero to nine are familiar to us and are used in various combinations to represent larger numbers.
Step 6: Counting Forwards
Counting forwards involves moving from a lower number to a higher number. For example, starting from one and moving up to nine. This is the natural order of numbers and helps in understanding the sequence and progression of numbers. Counting forwards is a straightforward process that involves incrementing the number by one each time.
Step 7: Practical Example
Let's consider a practical example to illustrate counting forwards. Imagine you are at a dog park and see four dogs. You start counting from one: the first dog is one, the second dog is two, the third dog is three, and the fourth dog is four. By counting each dog once and starting from one, you determine that there are four dogs at the park.
Step 8: Conclusion
In conclusion, counting forwards is a simple yet essential skill that helps us understand numbers and their order. By starting with one, assigning numbers to objects, and counting each object once, we can accurately determine the total number of objects. This process is fundamental in various aspects of life and forms the basis of more complex mathematical concepts.
FAQs
Here are some frequently asked questions about counting forwards:
1. Why is counting forwards important for children to learn?
Counting forwards is crucial for children as it forms the foundation of mathematical understanding. It helps develop number sense, prepares them for addition and other arithmetic operations, and is essential for everyday activities like keeping score in games or handling money.
2. How can I help my child practice counting forwards at home?
You can incorporate counting into daily activities such as counting steps while walking, objects around the house, or items while grocery shopping. Fun games like hopscotch, using a counting jar, or playing dice games can also make practice enjoyable.
3. What is the relationship between counting forwards and addition?
Counting forwards is essentially a series of additions by one. When children learn to count forwards, they are laying the groundwork for understanding addition. For example, adding 3 + 4 can be thought of as counting forward 4 steps from 3.
4. How does a number line help in understanding counting forwards?
A number line visually represents the sequence of numbers, making it easier to understand the concept of increasing values. Moving to the right on a number line corresponds to counting forwards, helping children grasp the idea that each step represents an increase by one.
5. At what age should children typically master counting forwards to 100?
While development varies among children, most can count to 100 by age 6 or 7. However, the foundations of counting typically begin around age 2 or 3 with small numbers, gradually progressing to larger numbers as the child develops. Consistent practice and engagement with numbers in everyday life can help children master this skill.
Prerequisite Topics for Counting Forwards
Understanding the foundations of mathematics is crucial for mastering more advanced concepts. When it comes to counting forwards, several prerequisite topics play a vital role in building a solid understanding. Let's explore how these topics interconnect and contribute to your ability to count forwards effectively.
One of the fundamental skills related to counting forwards is path counting problems. This concept involves counting objects in various arrangements, which directly relates to the process of counting forwards. By practicing path counting problems, students develop a stronger sense of numerical sequences and patterns, essential for progressing in their counting skills.
Another critical prerequisite is comparing and ordering numbers. This skill is indispensable when counting forwards, as it helps students understand the relationship between numbers and their relative positions in a sequence. Being able to compare and order numbers, including negative numbers, provides a comprehensive framework for counting in both positive and negative directions.
The concept of place value is equally important in the context of counting forwards. Understanding place values allows students to grasp the structure of our number system, making it easier to count larger numbers and recognize patterns in numerical sequences. This knowledge is particularly useful when transitioning from counting single digits to multi-digit numbers.
By mastering these prerequisite topics, students build a strong foundation for counting forwards. Path counting problems enhance the ability to visualize and manipulate numerical sequences. Comparing and ordering numbers develop a sense of numerical relationships, crucial for understanding the progression of numbers when counting forwards. Place value knowledge provides the structural understanding necessary for working with larger numbers and recognizing patterns in counting sequences.
Moreover, these prerequisite skills are interconnected. For instance, understanding place values aids in comparing and ordering numbers, which in turn supports more complex counting tasks. Similarly, the skills developed through path counting problems can be applied to understanding the logical progression of numbers when counting forwards.
As students progress in their mathematical journey, these foundational concepts continue to play a crucial role. They form the basis for more advanced mathematical operations and problem-solving skills. Therefore, investing time in mastering these prerequisites not only enhances the ability to count forwards but also paves the way for success in more complex mathematical concepts in the future.
In conclusion, a solid grasp of path counting problems, comparing and ordering numbers, and place value is essential for proficiency in counting forwards. These prerequisite topics provide the necessary tools and understanding to approach counting with confidence and accuracy, setting a strong foundation for future mathematical learning.

