Classifying polygons
Topic Notes
In this lesson, we will learn:
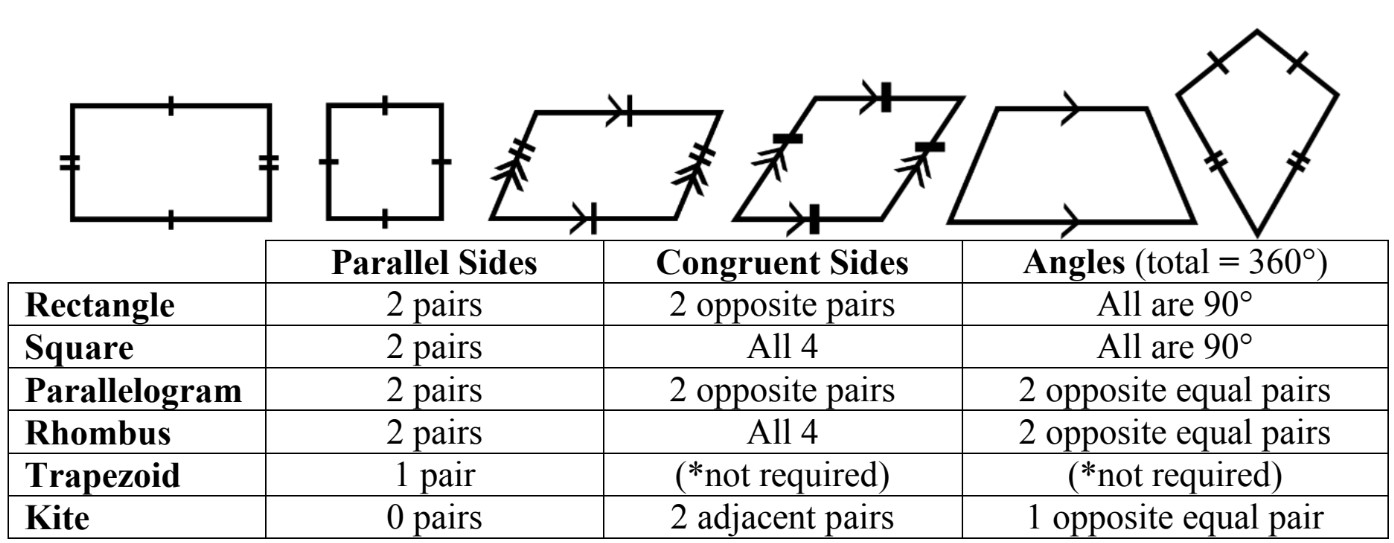
- A quadrilateral is a polygon with 4 sides
- We can look at the properties of a quadrilateral (pairs of parallel sides, pairs of congruent sides, types of angles) to classify into 6 different types
- The special types of quadrilaterals are: rectangle, square, parallelogram, rhombus, trapezoid, and kite
Notes:
- A quadrilateral is a 2D shape with 4 straight sides (a 4-sided polygon)
- A quadrilateral also has 4 vertices (corners)
- Each corner contains an angle; the total angle sum in any quadrilateral is 360°
- There are special quadrilaterals with specific definitions and names
- There will be 6 types of quadrilaterals in this lesson: Rectangle, Square, Parallelogram, Rhombus, Trapezoid, and Kite
- A quadrilateral can fit the definition of more than one of these special types
- Rectangles and squares:
- Quadrilaterals with 4 right angles (all angles are 90° )
- A rectangle has 2 pairs of opposite and equal sides (congruent)
- A square is a special type of rectangle where all 4 sides are equal (congruent)
- All squares are rectangles, but not all rectangles are squares
- Rectangles and squares can also be considered as parallelograms, just with right angles
- Parallelograms and rhombuses:
- Quadrilaterals with 2 pairs of parallel sides and 2 pairs of opposite equal angles
- A parallelogram has 2 pairs of congruent sides (equal length)
- A rhombus has all 4 sides congruent (all 4 sides equal length)
- All rhombuses are parallelograms; not all parallelograms are rhombuses
- Trapezoids:
- Quadrilaterals with only 1 pair of parallel sides
- Kites:
- Quadrilaterals with 2 adjacent congruent sides (no parallel sides)
- There is 1 pair of opposite equal angles across the line of symmetry
- Summary of quadrilateral types and properties (sides and angles):
Introduction to Classifying Quadrilaterals
Welcome to our exploration of quadrilaterals! These fascinating 2D shapes are four-sided polygons that come in various forms. In our introduction video, we'll dive into the world of quadrilaterals and their classification, which is crucial for understanding geometry. As your math tutor, I'm excited to guide you through this topic. We'll start by defining what makes a shape a quadrilateral and then move on to the different types, such as rectangles, squares, parallelograms, and trapezoids. Each has unique properties that set it apart. Understanding these classifications will help you recognize and analyze shapes in the world around you. The video will provide visual examples and clear explanations, making it easier to grasp these concepts. Remember, mastering quadrilaterals is a key step in your geometry journey, so let's dive in and have fun exploring these four-sided wonders together!
Understanding Quadrilaterals
What is a Quadrilateral?
A quadrilateral is a two-dimensional geometric shape with four sides, four vertices (corners), and four angles. The word 'quadrilateral' comes from the Latin words 'quadri-', meaning 'four', and 'latus', meaning 'side'. This simple yet versatile shape is found abundantly in our everyday surroundings and forms the basis for many more complex geometric concepts.
Basic Properties of Quadrilaterals
All quadrilaterals share some fundamental properties:
- They have four sides, which can be of equal or different lengths.
- They have four vertices where the sides meet.
- They have four interior angles.
- The sum of their interior angles is always 360 degrees.
- They are closed shapes, meaning their sides form a continuous loop.
Quadrilaterals in Everyday Life
Once you start looking, you'll find quadrilaterals everywhere! Some common examples include:
- The screens of our smartphones, tablets, and televisions
- Most picture frames and photographs
- The pages of books and notebooks
- Windows and doors in buildings
- Traffic signs, especially warning and regulatory signs
- The faces of dice used in board games
The Internal Angle Sum: A Special Property
One of the most fascinating properties of quadrilaterals is that the sum of their internal angles is always 360 degrees. This holds true regardless of the quadrilateral's shape or size. Whether it's a perfect square, a long rectangle, or an irregular four-sided shape, if you add up all four interior angles, you'll always get 360 degrees.
This property can be proven mathematically and has practical applications in fields like architecture, engineering, and design. Understanding this concept helps in solving problems related to quadrilaterals and in creating accurate geometric constructions.
Types of Quadrilaterals
While all quadrilaterals share basic properties, there are several specific types, each with unique characteristics:
- Squares: All sides equal, all angles 90 degrees
- Rectangles: Opposite sides equal, all angles 90 degrees
- Parallelograms: Opposite sides parallel and equal
- Rhombuses: All sides equal, opposite angles equal
- Trapezoids: One pair of parallel sides
- Kites: Two pairs of adjacent sides equal
Conclusion
Quadrilaterals are more than just simple four-sided shapes. They are fundamental geometric figures with properties that make them essential in mathematics and everyday life. From the screens we view to the rooms we live in, quadrilaterals surround us, showcasing the beautiful intersection of mathematics and the physical world. Understanding these shapes and their properties opens up a world of geometric exploration and practical applications.
Key Geometry Terms for Classifying Quadrilaterals
Understanding the fundamental geometry terms used in classifying quadrilaterals is essential for mastering this area of mathematics. Let's explore five crucial terms: congruent, opposite, adjacent, parallel, and perpendicular. These concepts play a vital role in identifying and describing various types of quadrilaterals.
Congruent
In geometry, congruent means exactly equal in size and shape. When we talk about congruent elements in quadrilaterals, we're referring to sides or angles that have the same measurements. For example, in a rectangle, the opposite sides are congruent. This means that the two longer sides have the same length, and the two shorter sides are also equal in length. Similarly, all four angles in a rectangle are congruent, each measuring 90 degrees.
Opposite
In quadrilaterals, opposite refers to elements that are across from each other. This term is often used to describe sides or angles that are not adjacent. For instance, in a parallelogram, the opposite sides are parallel and congruent. The angles opposite each other in a parallelogram are also congruent. In a kite, the opposite angles at the non-vertex ends are congruent, while the other pair of opposite angles are not.
Adjacent
Adjacent means next to or beside. In quadrilaterals, adjacent sides share a common endpoint, and adjacent angles share a common side. For example, in any quadrilateral, each side is adjacent to two other sides, and each angle is adjacent to two other angles. In a square, adjacent sides are perpendicular to each other, forming right angles. Understanding the concept of adjacency is crucial when analyzing the properties of different quadrilaterals and their relationships.
Parallel
Parallel lines are lines that never intersect, no matter how far they are extended. In quadrilaterals, parallel sides are a key feature of certain shapes. Parallelograms, including rectangles and squares, have two pairs of parallel sides. In a trapezoid, only one pair of opposite sides is parallel. The presence of parallel sides affects the angles within the quadrilateral. For instance, in a parallelogram, opposite angles are congruent because of the parallel sides.
Perpendicular
Perpendicular lines intersect at right angles (90 degrees). In quadrilaterals, perpendicular sides create right angles within the shape. Rectangles and squares have all four sides meeting at right angles, making each pair of adjacent sides perpendicular. In a kite, the diagonals are perpendicular to each other. Understanding perpendicularity is crucial for identifying and constructing various quadrilaterals, especially those with right angles.
These geometry terms - congruent, opposite, adjacent, parallel, and perpendicular - are fundamental in classifying and describing quadrilaterals. Congruence helps us identify equal parts, while understanding opposite and adjacent elements allows us to analyze relationships within the shape. Parallel and perpendicular properties define specific types of quadrilaterals and influence their overall structure.
For example, a square combines all these concepts: it has four congruent sides, two pairs of parallel sides, four right angles formed by perpendicular adjacent sides, and opposite sides that are both parallel and congruent. A rhombus, on the other hand, has four congruent sides and two pairs of parallel sides, but its angles are not necessarily right angles.
By mastering these terms, you'll be better equipped to analyze, describe, and classify various quadrilaterals. Remember that these concepts often work together to define the unique properties of each quadrilateral type. Practice identifying these elements in different shapes to reinforce your understanding and improve your geometric reasoning skills.
Rectangles and Squares
Let's dive into the fascinating world of quadrilaterals, specifically focusing on rectangles and squares! These shapes are special types of four-sided figures that we encounter in our daily lives, from the pages of a book to the screens of our devices.
First, let's talk about rectangles. A rectangle is a quadrilateral with four right angles. Imagine drawing a shape where all the corners are perfect 90-degree angles - that's a rectangle! One of the key properties of rectangles is that they have two pairs of parallel sides. This means that the opposite sides are always the same distance apart, no matter how long or short they are.
Picture a door frame or a television screen. These are perfect examples of rectangles in the real world. The top and bottom sides are parallel to each other, as are the left and right sides. This parallel nature gives rectangles their distinctive shape and makes them incredibly useful in architecture and design.
Now, let's move on to squares. A square is a special type of rectangle - you could say it's a rectangle's more symmetrical cousin! Like rectangles, squares have four right angles, but they have an additional property that makes them unique: all four sides are exactly the same length, or congruent.
Think of a chess board or a perfectly shaped cookie. These are great examples of squares. The equal side lengths give squares a perfect symmetry that's pleasing to the eye and useful in many applications, from tile layouts to computer icons.
The relationship between rectangles and squares is quite interesting. Every square is a rectangle, but not every rectangle is a square. This is because squares meet all the criteria of rectangles (four right angles, two pairs of parallel sides) while also having the additional property of four congruent sides.
To visualize this, imagine you have a stretchy rubber band in the shape of a square. If you pull it evenly on two opposite sides, it will become a rectangle, maintaining its right angles and parallel sides. However, it's no longer a square because the sides are no longer all the same length.
Both rectangles and squares have some fantastic properties that make them special. For instance, the diagonals of both shapes bisect each other, meaning they cross at their midpoints. In a rectangle, these diagonals are equal in length, while in a square, they're not only equal but also perpendicular to each other, forming four right angles at the center.
These shapes are incredibly important in mathematics and the world around us. Rectangles are often used in design due to their pleasing proportions and efficiency in space usage. Squares, with their perfect symmetry, are frequently used in logos, patterns, and architectural elements.
Next time you're out and about, try to spot rectangles and squares in your environment. You might be surprised at how often these shapes appear in buildings, furniture, technology, and even in nature. Understanding these shapes and their properties can help you appreciate the geometry that surrounds us every day!
Parallelograms and Rhombuses
Parallelograms and rhombuses are fascinating shapes in geometry that share many properties while maintaining their unique characteristics. Let's explore these quadrilaterals and understand their relationship to each other.
A parallelogram is a four-sided figure with two pairs of parallel sides. This means that opposite sides are always parallel to each other. One of the most striking features of a parallelogram is that its opposite sides are not only parallel but also congruent, meaning they have the same length. This property gives parallelograms their distinctive shape, often described as a "slanted rectangle."
When we look at the angles of a parallelogram, we find another interesting property: opposite angles are congruent. This means that the angles at opposite corners of the parallelogram are equal. Additionally, adjacent angles in a parallelogram are supplementary, which means they add up to 180 degrees.
Now, let's turn our attention to the rhombus, a special type of parallelogram. A rhombus is defined as a quadrilateral with four congruent sides. This means that all four sides of a rhombus have the same length. Because of this property, a rhombus is sometimes referred to as an "equilateral quadrilateral."
The relationship between parallelograms and rhombuses is quite interesting. Every rhombus is a parallelogram, but not every parallelogram is a rhombus. This is because a rhombus meets all the criteria of a parallelogram (parallel opposite sides, congruent opposite sides, and congruent opposite angles) while also having the additional property of all sides being congruent.
In a rhombus, not only are the opposite angles congruent (as in all parallelograms), but the diagonals are perpendicular to each other and bisect each other. This means that if you draw lines connecting opposite corners of a rhombus, these lines will cross at right angles and divide each other into two equal parts.
To visualize these shapes, imagine a parallelogram as a pushed-over rectangle. Its opposite sides remain parallel, but it leans to one side. A rhombus, on the other hand, can be thought of as a square that has been stretched or compressed diagonally. It maintains equal side lengths but can have angles that aren't right angles.
In everyday life, we can find examples of parallelograms and rhombuses all around us. The side view of a leaning bookshelf might resemble a parallelogram, while a diamond-shaped road sign is a perfect example of a rhombus. In architecture, parallelogram shapes are often used in modern building designs to create interesting visual effects, while rhombus patterns can be found in various decorative elements, from floor tiles to fabric designs.
Understanding these shapes is crucial in many fields, including engineering, architecture, and design. The properties of parallelograms and rhombuses make them useful in various applications, from constructing stable structures to creating aesthetically pleasing patterns.
In conclusion, while parallelograms and rhombuses share many properties, including parallel sides and congruent opposite angles, the rhombus stands out with its four congruent sides. This special relationship makes the study of these shapes both intriguing and valuable in geometry and beyond. Whether you're a student learning about these shapes for the first time or an enthusiast revisiting these concepts, the world of parallelograms and rhombuses offers a fascinating glimpse into the beauty and precision of geometric forms.
Trapezoids and Kites
Let's dive into the fascinating world of quadrilaterals and explore two unique shapes: trapezoids and kites. These special four-sided figures have some interesting properties that set them apart from other shapes.
First, let's talk about trapezoids. A trapezoid is a quadrilateral with at least one pair of parallel sides. These parallel sides are called the bases of the trapezoid. The non-parallel sides are referred to as the legs. Imagine a shape that looks like a table top that's a trapezoid! The parallel sides can be of different lengths, which gives trapezoids their distinctive appearance.
One of the most interesting properties of trapezoids is the trapezoid midsegment theorem. This states that the line segment connecting the midpoints of the non-parallel sides is parallel to the bases and its length is the average of the lengths of the bases. It's like having a mini-trapezoid inside the larger one!
Now, let's consider a special type of trapezoid called an isosceles trapezoid. In this case, the non-parallel sides (legs) are of equal length. Picture a trapezoid with a mirror-like symmetry that's an isosceles trapezoid. These shapes have some cool properties, such as equal base angles and congruent diagonals.
Moving on to kites, these quadrilaterals have a unique and eye-catching shape. A kite is defined by having two pairs of adjacent sides that are congruent (equal in length). If you've ever flown a kite, you'll recognize this shape immediately! The longer diagonal of a kite bisects the shorter diagonal at right angles, creating some interesting geometric relationships.
One of the key properties of kites is that they have at least one pair of congruent opposite angles. This occurs where the pairs of congruent sides meet. Additionally, the diagonals of a kite are perpendicular to each other, forming four right angles at their intersection point.
To help visualize these shapes, imagine a trapezoid as a pizza slice with the pointy end cut off, creating a flat top. For a kite, think of two triangles joined at their bases, forming a diamond-like shape. These mental images can make it easier to understand and remember the properties of these quadrilaterals.
Both trapezoids and kites play important roles in geometry and have practical applications in the real world. Trapezoids are often seen in architecture, such as in the design of roofs or bridges. Kites, besides being fun flying toys, inspire designs in various fields, from aviation to art.
As you explore these shapes further, you'll discover even more interesting properties and relationships. For example, did you know that the area of a trapezoid can be calculated using the formula A = (a+b)h/2, where a and b are the lengths of the parallel sides and h is the height? Or that the area of a kite is simply half the product of its diagonals?
Whether you're studying geometry for school or just curious about shapes, trapezoids and kites offer a wealth of fascinating concepts to explore. Their unique properties and visual appeal make them stand out in the world of quadrilaterals. So next time you see a table top or fly a kite, remember the special geometric principles at work!
Classifying Quadrilaterals: A Review
Quadrilaterals are four-sided polygons that come in various shapes and sizes. Understanding their special classifications is crucial in geometry. Let's explore the six main types of quadrilaterals and their unique properties.
The Six Special Quadrilaterals
- Square: All sides equal, all angles 90°
- Rectangle: Opposite sides equal, all angles 90°
- Rhombus: All sides equal, opposite angles equal
- Parallelogram: Opposite sides parallel and equal
- Trapezoid: One pair of parallel sides
- Kite: Two pairs of adjacent sides equal
Comparison Table of Quadrilateral Properties
| Property | Square | Rectangle | Rhombus | Parallelogram | Trapezoid | Kite |
|---|---|---|---|---|---|---|
| All sides equal | ||||||
| All angles 90° | ||||||
| Opposite sides parallel | One pair | |||||
| Diagonals bisect each other |
Identifying Quadrilaterals: A Decision Tree
To identify a quadrilateral, follow these steps:
- Are all sides equal?
- If yes, are all angles 90°? If so, it's a Square. If not, it's a Rhombus.
- If no, proceed to step 2.
- Are opposite sides parallel?
- If yes for both pairs, are all angles 90°? If so, it's a Rectangle. If not, it's a Parallelogram.
- If yes for only one pair, it's a Trapezoid.
- If no, proceed to step 3.
- Are two pairs of adjacent sides equal? If yes, it's a Kite.
Understanding these classifications and their properties is essential for solving geometric problems and recognizing shapes in real-world applications. Practice identifying these quadrilaterals to enhance your spatial reasoning skills and geometric understanding.
Conclusion
Classifying quadrilaterals is a fundamental skill in geometry that opens doors to deeper mathematical understanding. By mastering the distinctions between parallelograms, rectangles, squares, rhombuses, and trapezoids, you're building a solid foundation for more advanced geometric concepts. Remember, each quadrilateral has unique properties that set it apart, from parallel sides to equal angles. This knowledge isn't just theoretical; it has practical applications in fields like architecture, design, and engineering. As you continue your geometry journey, challenge yourself to identify quadrilaterals in everyday life. Practice sketching different types and explore how changing one property affects the entire shape. Don't be discouraged if it seems complex at first with consistent practice and exploration, you'll soon find yourself confidently navigating the world of quadrilateral classification. Keep up the great work, and let your curiosity drive you to discover even more fascinating aspects of geometry!
FAQs
-
What is a quadrilateral?
A quadrilateral is a two-dimensional geometric shape with four sides, four vertices (corners), and four angles. The word 'quadrilateral' comes from the Latin words 'quadri-' (four) and 'latus' (side). All quadrilaterals have a sum of interior angles equal to 360 degrees.
-
What are the main types of quadrilaterals?
The main types of quadrilaterals are: - Square: All sides equal, all angles 90° - Rectangle: Opposite sides equal, all angles 90° - Rhombus: All sides equal, opposite angles equal - Parallelogram: Opposite sides parallel and equal - Trapezoid: One pair of parallel sides - Kite: Two pairs of adjacent sides equal
-
How can I distinguish between a rectangle and a square?
Both rectangles and squares have four right angles (90°). The key difference is that a square has all four sides equal in length, while a rectangle has two pairs of equal sides. All squares are rectangles, but not all rectangles are squares.
-
What is special about a parallelogram?
A parallelogram has two pairs of parallel sides. Its opposite sides are equal in length, and its opposite angles are congruent. The diagonals of a parallelogram bisect each other. Rectangles, squares, and rhombuses are all special types of parallelograms.
-
How is a trapezoid different from other quadrilaterals?
A trapezoid is unique among quadrilaterals because it has exactly one pair of parallel sides, called bases. The non-parallel sides are called legs. If the legs are equal in length, it's an isosceles trapezoid. Trapezoids don't have all the symmetrical properties of parallelograms but have their own special characteristics, like the trapezoid midsegment theorem.
Prerequisite Topics for Classifying Quadrilaterals
Understanding the classification of quadrilaterals is a crucial skill in geometry, but to truly master this concept, it's essential to have a solid foundation in several prerequisite topics. These fundamental areas of study provide the necessary background knowledge to comprehend and apply the principles of quadrilateral classification effectively.
One of the most important prerequisite topics is polygons. Quadrilaterals are a specific type of polygon, and understanding the general properties of polygons is crucial. For instance, knowing how to calculate the interior angles sum of a polygon is fundamental when analyzing quadrilaterals. This knowledge allows students to recognize that all quadrilaterals have an interior angle sum of 360 degrees, which is a key characteristic in their classification.
Another vital prerequisite topic is the understanding of right angles. While this concept is often associated with trigonometry, it plays a crucial role in classifying quadrilaterals. Many types of quadrilaterals, such as rectangles and squares, are defined by their right angles. Being able to identify and work with right angles is essential for accurately categorizing these shapes.
The study of parallel and perpendicular lines is another prerequisite that directly relates to quadrilateral classification. Many quadrilaterals are defined by the relationships between their sides. For example, parallelograms have two pairs of parallel sides, while rectangles have two pairs of parallel sides and four right angles. Understanding how to identify and work with perpendicular lines is particularly important for recognizing and classifying shapes like squares and rectangles.
By mastering these prerequisite topics, students build a strong foundation for understanding quadrilaterals. The knowledge of polygons provides the broader context for quadrilaterals, while familiarity with right angles and parallel and perpendicular lines allows for precise classification. These concepts intertwine to form a comprehensive understanding of quadrilateral properties and characteristics.
As students progress in their study of geometry, they'll find that these prerequisite topics continue to be relevant. The principles learned in studying polygons, right angles, and parallel and perpendicular lines extend beyond just classifying quadrilaterals. They form the basis for more advanced geometric concepts and problem-solving techniques.
In conclusion, a thorough grasp of these prerequisite topics is not just beneficial but essential for anyone looking to excel in classifying quadrilaterals. By investing time in understanding these foundational concepts, students set themselves up for success in more advanced geometric studies and develop critical thinking skills that are valuable across various mathematical disciplines.

